数学进化中的知识发现方法
2011-08-18陈文伟黄金才陈晟
陈文伟,黄金才,陈晟
(1.海军兵种指挥学院 三系,广东 广州 510431;2.国防科技大学 C4ISR技术国防科技重点实验室,湖南 长沙 410073;3.东南融通系统工程有限公司测试业务线,北京 100013)
数学进化中的知识发现方法
陈文伟1,2,黄金才2,陈晟3
(1.海军兵种指挥学院 三系,广东 广州 510431;2.国防科技大学 C4ISR技术国防科技重点实验室,湖南 长沙 410073;3.东南融通系统工程有限公司测试业务线,北京 100013)
从数学历史发展过程中去发现数学的进化规律,从创造数学符号和包容对立的概念中获得了最早的数学知识.将数学符号组合而成的表达式和方程,使问题变换成了形式化表示,当表达式和方程通过推演和求证,判断其正确性时,就形成了公式和定理,它们是数学中的基础理论.推演和求证过程是采用了等价变换.数学进化中更重要的知识发现方法是利用进化变换(对变量、函数、方程、方法等的变换)来拓展数学的新概念和解决不能求解的问题(可拓变换),从而建立了数学的理论体系.创造、包容、形式化变换、等价变换和进化变换都是数学进化中的知识发现方法.
数学进化;知识发现;创造法;包容法;形式化变换;等价变换;进化变换
数学的进化发展是一个不断创新的过程.现已出版的各种关于数学发展史的书籍都是介绍各个时期所发现的新知识以及它的价值[1],很少有人去研究数学发展中是否存在进化规律.本文试探研究数学进化中的知识发现方法,以便启发人们去理解和思考这些方法,并进一步去寻找更多的知识发现方法[2],这样,人们能更清晰地掌握和促进数学的发展过程.这是一种新的尝试,希望能引起大家的关注.
1 数学进化综述
数学经过几千年的进化发展,笔者从以下3个方面来分析数学的进化过程.
1.1 数学本质的进化
数学本质的进化过程可以简单地表述为[1]:
数学概念→初等数学→变量数学→现代数学→计算数学.
数学概念时期主要是建立了自然数和简单的计算;初等数学时期主要有算术、几何、代数、三角等;变量数学时期主要有函数、微积分、概率论等;现代数学时期主要有非欧几何、向量、群论、线性代数、集合论等.以上进化过程是建立在严格的逻辑推理基础的解析求解,笛卡尔指出,唯有数学证明是最科学和最严密的.
计算数学时期主要是利用计算机对数学问题进行数值求解,它开始是用来解决不能进行解析求解的问题.随着计算机的发展,所有的数学问题都可以进行数值求解,这极大地推动了数学在自然科学和社会科学的应用,使人类社会进入了信息化社会.
1.2 数学符号表示的进化
数学符号表示使数学问题简化,它是数学进化的基础,数学符号进化过程可以表述为
数字→算术→符号→表达式→方程式→图形→程序.
数字是数学的原始表示,主要是印度-阿拉伯数字:0、1、2、3、4、5、6、7、8、9;数学符号包括:特定数字(e、π、∞)、变量(x、y、z)、运算(+、-、×、÷)、关系(=、<、>、∽、∧、∨)、结合({}、())、省略(∵ 、log、∑、!)等符号,它们极大地推动了数学的发展;公式和方程式是用数学符号组合而形成的,它是数学中最重要的表示形式;图形是空间的表现形式,主要用于解析几何和拓扑学中;程序是计算机解决数学问题的表示形式.
1.3 数学理论的形成
数学理论的形成过程可以概括为
形式化表示→推演求证→公式和定理→理论体系.
数学问题用表达式或方程式(数学符号的组合)进行表示,实质上完成了“从数学问题到形式化表示的转换”.形式化表示是数学进化的最重要方法之一,它省去了问题的内容,形成了既直观又简单的有效表示方式[3].它便于推演与求证,即利用等价变换,得到正确的公式或者证明了定理.这种抽去了内容的正确结论,具有通用性,形成了数学理论[4].数学中各门类的理论集合,形成了数学的理论体系.
2 数学进化的知识发现方法
2.1 创造法
创造法使数学从无到有,包括人类创造的数字、符号、图形、函数、微积分、方程等.
1)数字的创造.数字的创造有几千年的历史,阿拉伯、印度、中国等古老民族都创造出自己的数字,最后统一为印度-阿拉伯数字.
2)符号的创造与进化.表述为数字符号→ 运算符号→函数符号→微积分符号→方程表示.这些符号的创造形成了数学的形式化,极大地推动了数学的进化.
3)图形的创造与进化.表述为坐标图形→平面曲线→空间曲面→拓扑表示.这些图形的创造使数学更形象化了,数学家把这些图形用函数来表示,即把图形变换成函数来研究,产生了数学的新分支.
2.2 包容法
数学的进化得益于采用了包容法,它把矛盾的双方都包容共存下来,承认矛盾的双方都合理,把它们合起来构成一个新领域.典型表现在于数的进化和几何的进化,这是数学进化的重要特点.这种包容法称为包容变换(特殊的可拓加变换)[5],表示为

式中A和A-1是数学中相反的双方.
2.2.1 数的进化
数的进化是在不断创造新数[1],它与原来的数又存在矛盾,但采用包容法,承认矛盾的双方都合理,把双方都包容共存起来形成一个更大范围的新数.
数的进化过程表述为[1]
自然数→整数→有理数→无理数→实数→虚数→复数.
1)自然数与零(0)是矛盾的,正数与负数是矛盾的.自然数(正数)是有值的数,零(0)是无值的数,正好相反.正数与负数也是相反的.把它们都包容共存起来,构成新数即整数.用包容变换表示为
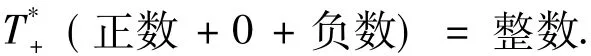
2)有理数与无理数的矛盾,用包容变换表示为

3)实数与虚数的矛盾,用包容变换表示为

以上包容变换完成了数的进化,使数成为了一个完整的整体.其中“0”本身是“一无所有”,但是它在记数中表示“空位”,它作为一个数可以参与运算,又是数轴上的起点和分界点,在数中发挥了重要的作用.还有虚数()最早是在方程式求根公式中出现,不被人看好,德国数学家高斯创立虚数的图解法,虚数的意义才逐渐明确.复数可以表示力、位移、速度等向量,有了实际意义,才为人们广泛承认.现在复变函数的理论在流体力学、热力学等方面有了广泛的应用.
2.2.2 几何的进化
几何的进化同样是不断地包容矛盾的双方才得以进步的.最早建立的比较严格的几何体系是欧几里德的几何.在欧氏几何中第5公理,设“给定一条直线l和不在直线上的一点P时,过点P作和直线l平行的直线m有且只有一条”,该公理不直观、难于验证.
罗巴切夫斯基作出与欧几里德几何第5公理相反的断言:通过直线外一点,可以引不止一条而至少是2条直线平行于已知直线,由此推导下去,他得到一系列前后一贯的命题,形成逻辑上没有任何矛盾的与欧氏几何完全不同的另外一种新几何系统,称罗巴切夫斯基非欧几何.
非欧几何与欧氏几何是相矛盾的.当时受到嘲笑,非欧几何在创立后的三四十年的时间内完全被学术界忽视.后来,黎曼建立了空间曲率概念,黎曼指出:如果设曲率为α,当α =0时,这个空间的模型便是欧氏平面几何;当α>0时,得到罗氏非欧几何;而对于α<0时,则是黎曼本人的创造,它对应于另一种非欧几何学,即黎曼几何.实际上,普通球面的几何就是黎曼非欧几何.并且,黎曼非欧几何与罗氏非欧几何在空间曲率上是相反的.
克莱因用“群”的观点来研究几何学,他认为,变换群的任何一种分类对应几何学的一种分类.这样,表面上互不相干的几何学就被联系在一起了,克莱因统一了几何学,后人称为克莱因几何.
包容法把几个矛盾的几何都包容进来了,极大促进了几何的进化.几何的进化用包容变换(特殊的可拓加变换)表示为

爱因斯坦提交的《引力场方程》的论文,标志广义相对论的诞生,文章提出的引力使光线弯曲的计算,正是引用了黎曼几何的数学表述.
2.3 形式化变换
各种数学符号的组合形成了表达式和方程,它用来描述数学问题,既简化了问题又便于推演.形式化表示[6]实质上实现了把问题的自然语言描述变换成了问题的形式化描述.这样极大地推动了数学的进化,把这种变换称为形式化变换.形式化变换表示为
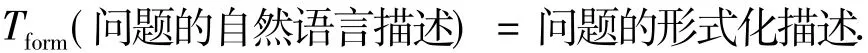
形式化变换是数学进化的重要里程碑.我国古代数学的发展较迟缓的一个重要原因在于没有把问题进行形式化变换,而西方数学的发展较快的原因正是得益于把数学问题进行了形式化变换.
2.4 等价变换
数学中一个重要的解题方法是用等价变换进行解析求解或者进行定理证明.等价变换不是相同变换,等价变换的前后会发生变化,要么是数学结构元素的变化,要么是数值的变化.
2.4.1 数学结构中元素变化的等价变换
数学中绝大多数的运算都是数学结构的元素发生变化的等价变换,即相等运算的元素前后都发生了变化.
例如,线代数方程组用矩阵表示为

线代数方程组利用消元法求解,通过对矩阵的元素进行选主元、主元归一、消元等步骤反复推演,最后得到具有单位矩阵的线性方程组,其中每一步相等运算前后的元素都发生了变化,最后得到的具有单位矩阵的线性方程组,即
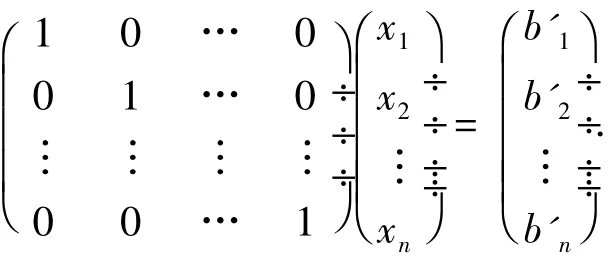
它和原始的线性方程组在数学结构的元素上发生巨大的变化,这时已经求出方程组的解.
2.4.2 数值变化的等价变换
数学中的迭代法的等价变换,其运算的前后都不发生数学结构元素的变化,但是发生数值的变化,经过成千上万次迭代,最后得到方程的解.
例如,BP神经网络中权值和阈值的求解的迭代算法.
1)网络权值的变换Tw:
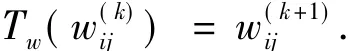
该变换的计算公式为
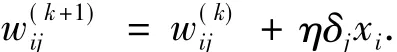
2)阈值的变换Tθ:

该变换的计算公式为
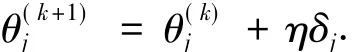
迭代公式每次迭代时公式形式不会发生变化,但每次迭代时元素的值在发生变化.
数学中的等价变换是解决“未知”与“已知”的问题.等价变换是在数学原理(定义、定理等)或数学方法(消去法、迭代法等)的指导下进行的,通过等价推演或相等计算来完成从“未知”到“已知”的转变[7].
2.5 进化变换
2.5.1 新概念的拓展
对变量的变换拓展出了函数的新概念,对函数的变换拓展出了导数和积分的新的概念等.这些拓展新概念的变换称为进化变换.
1)函数的出现与进化.
函数的创造使常量数学进入了变量数学.笛卡尔的几何学第一次涉及到变量,对变量的变换就形成了函数.函数是使变量x变换为变量y,变量y是随着变量x按照函数的关系而改变的.
函数的数学表达式和进化变换的表示分别为

函数的进化过程表述为
函数→初等函数→复合函数→复变函数→函数方程→特殊函数.
函数的创造在数学中是具有重要意义的标志或里程碑.数学家克莱因说,函数是数学思考和科学思考的心脏和灵魂.
2)微积分的出现与进化.
微分学研究物体运动的瞬时速度、曲线的切线、函数的极值等问题,积分学解决计算曲线所围成的面积、曲面所围成的体积、曲线长、物体的中心等问题.
微积分实质上是对函数的变换,即把一个函数变换成了另一个函数(导数或原函数),导数和积分的数学表达式和进化变换分别表示为:

微分和积分是数学的基础,也是科学发展的基石,对于无限的征服,成为了微分和积分发展的原动力.牛顿和莱布尼茨分别独立地建立了微积分学.
微积分的进化过程表述为
导数→微分→积分→常微分方程→偏微分方程→积分方程→变分方程.
导数表示当前变化的情况,积分表示长期积累的结果.微积分的创造是数学进化的重要里程碑.微积分的价值在于:用微分方程式表示自然现象和法则(多个变量变化时相互之间的关系)的内在本质.
2.5.2 解决不能求解的问题
把一个不能求解的问题通过变换,将原问题变成一个可求解的问题,在可拓学中称为可拓变换.对于数学中一些不能求解的问题,采用对方程的变换或者对表达式的变换,使问题变成能够求解[8],这种变换仍称为进化变换.
1)解析求解的拉普拉斯变换.
当微分方程求不出解析解时,可以利用拉普拉斯变换(Tl)把它变换成代数方程,对代数方程求解,就容易求出它的解,再利用拉普拉斯逆变换(),把代数方程的解变换成微分方程的解,从而解决原微分方程求不出解析解的矛盾.用进化变换表示为:

例如:求常微分方程y″+4y'+3y=e-t满足初始条件y(0)=y'(0)=1的特解.
设拉普拉斯变换为Tl[y(t)]=Y(p),对常微分方程的拉普拉斯变换为

对变换后的代数方程求解,得出解为
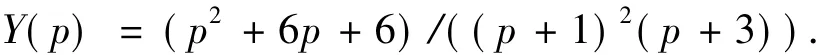
对此解进行拉普拉斯逆变换:[Y(p)]=y(t),得到常微分方程的解为
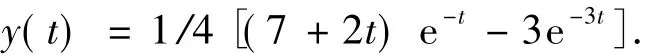
2)微分方程的差分变换.
所有不能进行解析求解的微分方程或积分方程,在变换成差分方程以后,都可以在计算机中进行数值求解.微分方程要进行数值求解,就必须进行差分化,也就是把微分方程变换成差分方程.用进化变换表示为
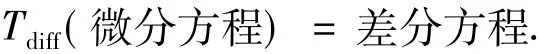
例如,偏微分方程:

经过差分化后,得到差分方程为

差分方程经过整理后,就形成了线代数方程组,在计算机中就可以进行数值计算了,最后求得偏微分方程的数值计算结果.
3)数值计算的表达式变换.
表达式有2种,一种进行算术运算,另一种进行导数求解.这2种表达式计算,都对运算符有个优先顺序的规定,算术运算的优先顺序原则是“先乘除,后加减,括号优先”;函数表达式求导数时,对运算符的优先顺序规定是,先对低级运算符号(+、-)求导数,再对高级运算符号(×、÷)求导数.这种人为规定,不适合在计算机中编程序完成,需要将表达式进行变换,把有优先顺序规定的表达式变换成只有前后顺序的表达式,这样才能编制程序在计算机中完成表达式的算术运算或求导数.
a)算术运算的逆波兰式变换.
这种变换实质上完成了表达式的中缀表达,变成了表达式的后缀表达,即逆波兰式.用进化变换表示为

例如:
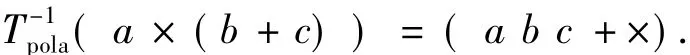
这样,后缀表达式对符号的算术运算就变成了先后顺序,既没有了括符,又没有了优先等级,编程序就很容易了.
b)求导数的波兰式变换.
这种变换实质上完成了函数表达式的中缀表达,变成了函数表达式的前缀表达,即波兰式.用进化变换表示为
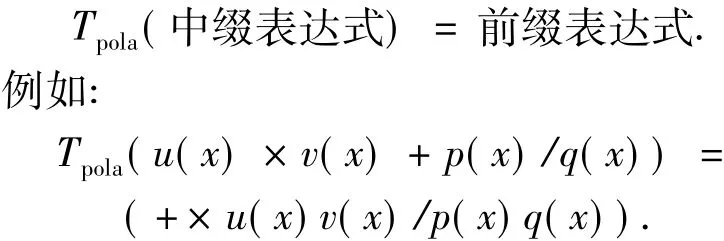
这样,对函数的前缀表达式求导数时,套用运算符号求导公式的顺序就一目了然了.
还有很多解决各种矛盾问题的变换这里就不多说明了.
2.5.3 方法的变换
在数学上,有大量的非线性方程和复杂的偏微分方程中是很难求出它的解析解.但是,将它们变换成数值求解方程后,即非线性方程变换成迭代方程,偏微分方程变换成差分方程,完成了从解析求解到数值求解的变换,问题就可以求解了.从解析求解到数值求解的变换,实质上是求解方法的变换,它使现代数学的理论求解变换成计算数学的数值求解.这是数学史中最大规模的一次进化,这种进化变换是对方法的变换,具体表示为

计算机的发展推动了计算数学的发展,计算数学属于数值计算,数值计算的发展又推动了非数值计算的发展(数据处理和知识推理),使计算机进入了人类社会,从而又推动了社会信息化进程.
3 结束语
数学是在不断提出新概念和解决矛盾中进化发展的,本文总结了数学进化中部分的知识发现方法,包括创造法、包容法、形式化变换、等价变换和进化变换(对变量、函数、方程、方法等的变换)来拓展数学的新概念和解决不能求解的问题(可拓变换).人们还需要进一步研究更多的知识发现新方法,既更深入了解数学进化规律,进一步促进数学的进化,数学的进化又将会推动社会的进步.
[1]张红.数学简史[M].北京:科学出版社,2007:145-275.
[2]陈文伟.挖掘变化知识的可拓数据挖掘研究[J].中国工程科学,2006,8(11):70-73.
CHEN Wenwei.The research of mining the mutative knowledge with extension data mining[J].Engineering Science,2006,8(11):70-73.
[3]陈文伟,杨春燕,黄金才.可拓知识与可拓知识推理[J].哈尔滨工业大学学报,2006,38(7):1094-1096.
CHEN Wenwei,YANG Chunyan,HUANG Jincai.Extension knowledge and extension knowledge reasoning[J].Journal of Harbin Institute of Technology,2006,38(7):1094-1096.
[4]陈文伟.基于本体的可拓知识链获取[J].智能系统学报,2007,2(6):68-71.
CHEN Wenwei.Acquisition of an extensional knowledge chain based on ontology[J].CAAI Transactions on Intelligent Systems,2007,2(6):68-71.
[5]杨春燕.可拓数据挖掘方法及其计算机实现[M].广州:广东高等教育出版社,2010:8-46.
[6]陈文伟,黄金才,毕季明.适应变化环境的元知识的研究[J].智能系统学报,2009,4(4):331-334.
CHEN Wenwei,HUANG Jincai,BI Jiming.A study on meta-knowledge suitable for a changing environment[J].CAAI Transactions on Intelligent Systems,2009,4(4):331-334.
[7]陈文伟,黄金才,毕季明.解决矛盾问题的可拓模型与可拓知识的研究[J].数学的实践与认识,2009,39(4):168-172.
CHEN Wenwei,HUANG Jincai,BI Jiming.The study of extension models and extension knowledge solving contradiction problems[J].Mathematics in Practice and Theory,2009,39(4):168-172.
[8]陈文伟,黄金才,毕季明.数学进化中矛盾问题的解决方法[J]. 智能技术学报,2010,2(1):72-78.
CHEN Wenwei,HUANG Jincai, BI Jiming.Knowledge mining of matchematic evolution approach[J].CAAI Transactions on Intelligence Technology,2010,2(1):72-78.

陈文伟,男,1940年生,教授,博士生导师,中国人工智能学会机器学习专业委员会副主任,中国人工智能学会可拓工程专业委员会副主任.主要研究方向为决策支持系统、机器学习、可拓工程、数据仓库与数据挖掘.曾获国家科技进步奖二等奖1项,军队科技进步奖二、三等奖8项,发表学术论文120余篇,出版专著10部.

黄金才,男,1972年生,教授,博士,中国人工智能学会机器学习专业委员会副主任,湖南青年系统工程与管理研究会副会长.主要研究方向为决策支持、数据挖掘和作战模拟,负责主持军队重点项目5项,获部委级科技进步奖4项,发表学术论文23篇,其中被EI检索13篇.

陈晟,男,1972年生,系统分析师,博士,主要研究方向为软件测试、软件工程、知识工程与知识管理,获部委级科技进步奖3项,发表学术论文20余篇,合作出版教材1部.
A knowledge discovery approach in the evolution of mathematics
CHEN Wenwei1,2,HUANG Jincai2,CHEN Sheng3
(1.The 3rd Department,Naval Command College,Guangzhou 510431,China;2.C4ISR Technology National Defense Technology Key Laboratory,National University of Defense Technology,Changsha 410073,China;3.Software Testing Department,Longtop System Engineering Corp.,Beijing 100013,China)
In this paper the mathematic evolution law is studied from the historical development of mathematics.The earliest knowledge of mathematics was acquired by creating mathematic symbols and the concepts of containment and contradiction.By combining mathematic symbols into expressions and equations,the problems are transformed into formalization descriptions.Expressions and equations become formulas and theorems when they are proven correct by simulations and proofs.Formulas and theorems are basic theories in mathematics.Simulations and proofs are equivalent transformations,while a more important knowledge discovery method in mathematic development is evolution transformation,such as transformation of variables,functions,formulas,and methods.These transformations extend new concepts and solve previously unsolvable problems.The theoretical system of mathematics is thereby constructed.Creation,containment,formalization transformation,equivalent transformation,and evolutional transformation are all knowledge discovery methods in the evolution progress of mathematics.
mathematic evolution;knowledge discovery;creation method;inclusion method;formalization transformation;equivalent transformation;evolutional transformation
TP311.13
A
1673-4785(2011)05-0391-05
10.3969/j.issn.1673-4785.2011.05.002
2010-12-18.
国家自然科学基金资助项目(70671031).
陈文伟.E-mail:chenww9@21cn.com.
