考虑个体移动和局域控制的SIR传染模型

赵敬，方义，夏承遗

(1.天津理工大学天津市智能计算与软件新技术重点实验室，天津 300384;2.天津理工大学教育部计算机视觉与系统重点实验室，天津 300384)

考虑个体移动和局域控制的SIR传染模型

赵敬1，2，方义1，2，夏承遗1，2

(1.天津理工大学天津市智能计算与软件新技术重点实验室，天津 300384;2.天津理工大学教育部计算机视觉与系统重点实验室，天津 300384)

为了能够有效地对疾病传播进行建模和分析，提出了带有个体移动性的考虑局部感染程度和局部控制程度的SIR模型，引入了感染半径和控制半径的概念.在二维平面空间的基础上，首先介绍了带有个体运动的模型，然后将此模型与改进的SIR模型结合，通过大量的数值仿真分析感染半径和控制半径对疾病传播的影响;同时，还利用数值仿真研究了移动个体密度和个体运动方向对疾病传播的影响;此外，基于改进的SIR模型提出了一些能够抑制疾病传播的直观控制策略，如对感染个体进行隔离、控制以及对人群进行疏散等.

个体移动;SIR模型;感染半径;控制半径

纵观人类社会的发展，传染病一直持续不断地阻碍着社会发展的进程，从早期的天花、麻疹，到近年来的艾滋病、非典型性肺炎(SARS)以及禽流感，每一次大爆发都给人们的生命财产带来巨大的损失［1－3］.一方面，人类社会的不断发展和完善促进了公共卫生体系的不断完善，从而降低了传染病的威胁;另一方面，社会快速发展的需求使得人力、物力资源流动日益频繁，从而加快了传染病的传播速度，增大了传染病的传播风险.在经历了一次次的考验之后，人们也不得不考虑:为什么在医疗水平如此发达的今天，传染病还会迅速传播?为什么在采取了病毒预防和控制措施后，计算机病毒还能在因特网上肆意地蔓延?经典的流行病学的研究将系统中所有个体划分成有限数目的仓室(如易感个体Susceptible、感染个体 Infective、免疫个体 Removed 等)，提出所谓的仓室模型(如SI、SIS和SIR模型等)，然后利用常微分方程组来建模和分析，虽然取得了骄人的成就，但仍然无法解决上述问题和困惑［4］.近年来，复杂网络理论的进展为传染病动力学的分析和研究提供了新的理论、工具和手段，使得复杂网络上的流行病传播成为生命科学、系统生物学、数理科学、信息科学与技术等领域的一个热点研究问题［5－7］.

基于复杂网络的传播动力学研究，假定每个节点代表一个独立的个体，节点之间的连线既代表两者之间有联系(熟人)，也代表了疾病传播的途径，即两者之间如果有一个感染者，那么和它有连线的另一个很可能会被感染.Pastor－Satorras等人［8］利用平均场理论研究了均匀网络和非均匀网络上的疾病传播行为，基于SIS模型他们发现均匀网络上疾病传播行为与经典传染模型类似，存在固定的与网络规模无关的正临界值(λc＞0);但是对于非均匀网络，在网络规模趋于无穷时(N→∞)感染临界值趋于0(λc→0)，这一突破性的进展改变了经典传染病动力学研究中许多固有的结论，激发了大量相关的研究［6－7，9－14］.

但是，目前的大多数研究仍是基于熟人之间的联系才可以传播，即假定网络结构固定不变.而实际生活之中个体之间不管是有连接(熟人)，还是无连接(陌生人)都是不确定的，熟人在疾病传播期间可能不相遇，陌生人在疾病传播期间可能有接触，例如商场、火车站等公共场所的服务人员每天可能接触成千上百的陌生人，他们原本都是陌生人，互相没有联系，但是在公共场所的某段时间内他们之间就会建立起新的连接.熟人之间的固定联系只能说明二者之间有疾病传染的可能性，疾病在人群中的传播不能仅仅考虑个体之间原有固定的联系，还应该考虑个体在物理空间的运动范围.因此，在真实网络中，个体之间的连接模式不断变化，研究复杂变化环境下的疾病传播行为具有重要的现实意义.文献［15］基于二维规则晶格，引入长程运动，允许个体以特定的概率pj在晶格上随机移动，建模个体在社会空间上的运动以及移动终端设备在通信网络中的移动，使得疾病在系统中的传播行为更加符合真实情况.文献［16］考虑了更一般的二维平面空间，假定个体在一个圆形的邻域范围内随机运动，并允许以特定的概率作长程跳跃，已感染疾病的个体可以感染给定半径内的易感个体.在此基础上，文献［17］考虑了个体运动的长程关联性.但是，上述研究也忽略了一些影响因素，例如在面临传染病爆发时，公共卫生部门会进行一定的干预和控制，会对感染个体周围进行适当的隔离措施，从而抑制疾病的进一步传播.本文拟提出一个同时考虑个体运动和局域控制策略的SIR模型，通过大量的数值仿真分析感染范围和接种疫苗范围对感染个体密度的影响，以建模分析公共卫生部门的控制策略的作用和影响.

1 个体运动模型

假定个体运动模型如图1所示，黑色的圆圈代表已感染的个体，白色的代表其他状态的个体，初始时，将N个智能体随机分配到L×L的满足周期边界条件的二维平面空间中，此时平面空间中的个体密度是ρ=N/L2.令vi和 θi(－π≤θ≤π )为第i个(i=1，2，…，N)个体的运动速度和方向，其中vi≈(vcos θi，vsin θi)即个体可以在二维平面空间上随机游走，方向和速度都是随机分配的.此外，个体还可以以一定的概率pj作(0≤pj≤1)长程运动.

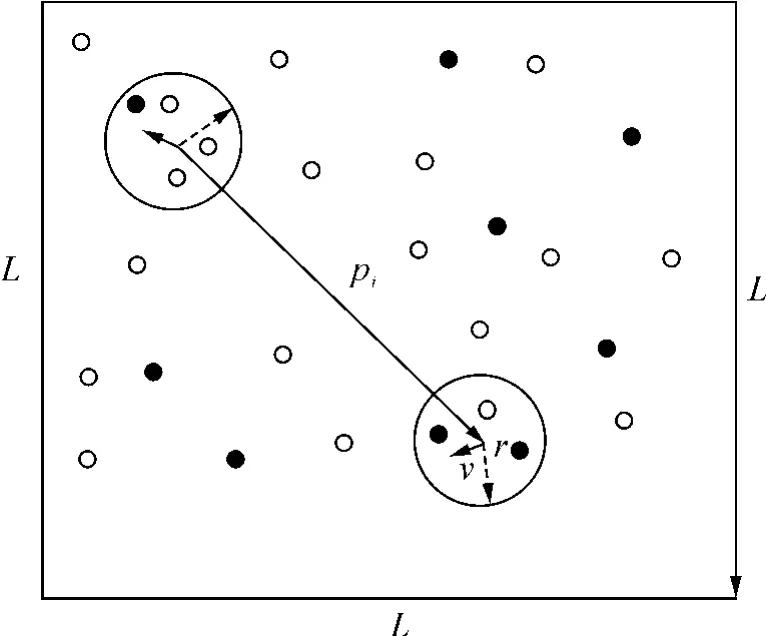
图1 个体运动模型Fig.1 Individual motion’s model

不同状态的个体运动形式也会有差别:1)感染者因为有传染性而被限制只能做局部运动，不能做长程运动，即pj=0;而其他状态的个体既可以做局部运动也可以做长程运动.2)未感染者对感染者有“趋利避害”的自适应性，若感染者在健康者的感染范围内，那么健康个体的运动方向θ不再是360°，本文假设未感染个体背离染病个体的方向在180°范围内随机运动，如图2所示.

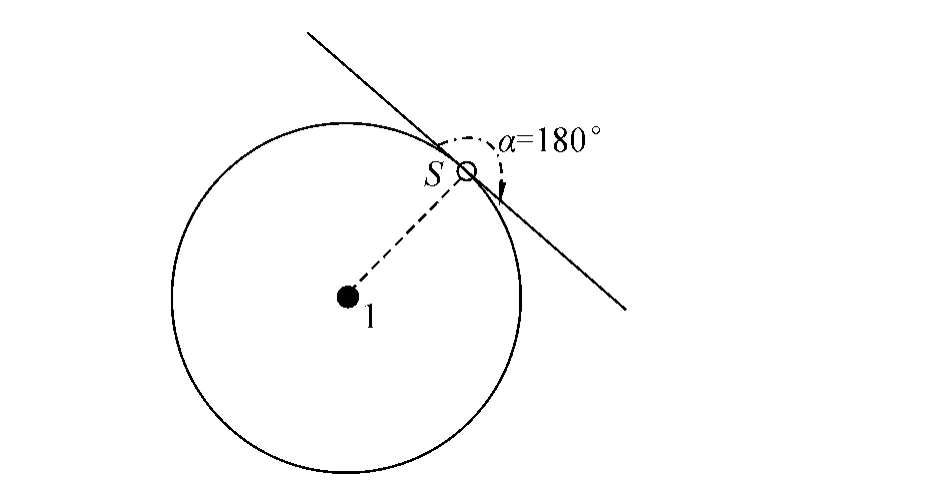
图2 个体移动方向示意Fig.2 Direction of individual motion

此外，考虑个体的“趋利避害”效应，进而会远离感染者，例如在图2中给出了个体移动方向的示意.当在一个未感染者(S，R)的一定范围内(例如r1=2)有感染者I，那么这个未感染者会按照背离感染者的方向(α=180°)移动.

2 考虑局域控制的改进SIR模型

在本文介绍的SIR模型中，假定个体可以处于5种状态，那么就可以把人群分为5类，如图3所示，它们分别是:易感染人群(S)、潜伏个体(E)、染病人群(I)、康复人群(R)和接种人群(V).另外，假定疾病传播过程中存在2个作用网络:传播网络和控制网络，控制网络是感染网络的子集，分别用感染半径(r1)和控制半径(r2)来定量刻画这2个网络，然后从微观上分析局部疾病传播程度和疾病控制程度对整体疾病传播的影响.

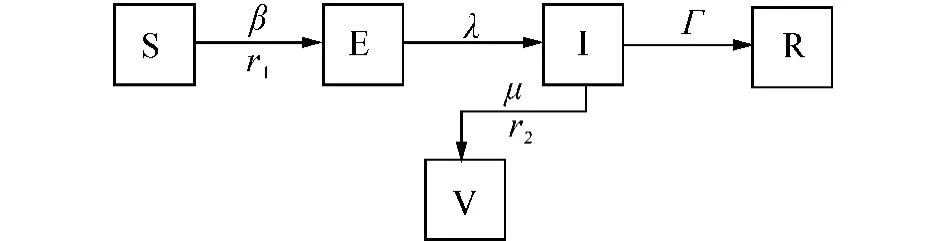
图3 改进的SIR状态Fig.3 The status of the improved SIR model

在图3所示模型中引入感染半径r1和控制半径r2的概念，如图4所示.

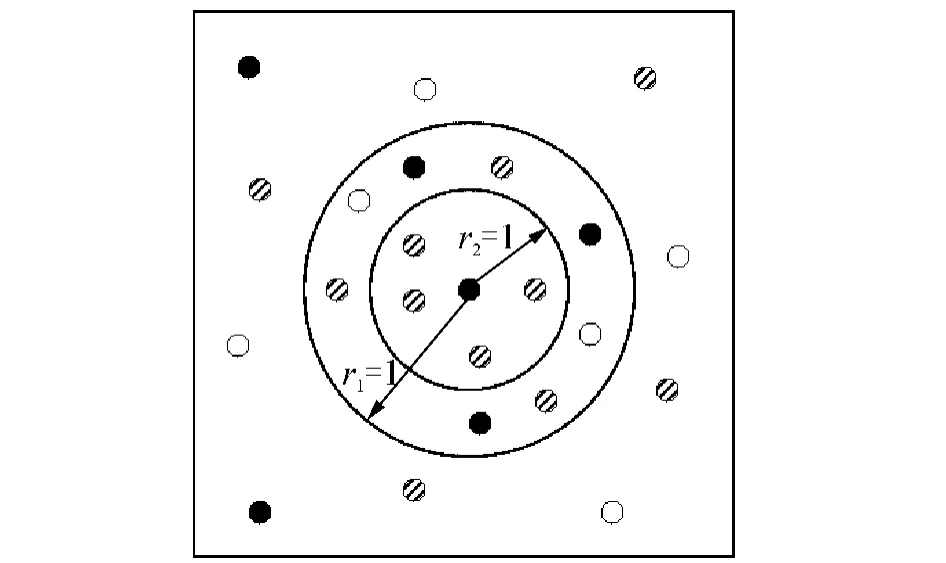
图4 感染半径r1和控制半径r2Fig.4 Infection radius r1and control radius r2

其中，黑色圆圈代表染病个体I，阴影圆圈代表接种个体V，白色圆圈代表其他状态的个体.易感染人群S不能感染其他人，但是有可能会被感染;潜伏个体E是已经染病且具有传染其他个体能力的，但是没有患病症状的人;染病人群I呈现患病症状且具有传染性，以概率β把疾病传染给以r1为半径的圆形范围内的易感染人群S，以概率γ被治愈进入康复状态R;另外，染病的个体I触发相应的控制动作，使其周围以r2为半径的圆形范围内的所有个体(不包括R状态个体)以概率μ被接种.

3 数值仿真结果

本节利用Matlab对改进的SIR模型进行数值分析，给出了一些典型参数条件下的仿真结果，以定量分析模型参数对传播行为的影响.在仿真实验中，模型参数设置如下:移动个体总数为N=10 000，感染率 β=0.1，治愈率 γ=0.1，接种率 μ=0.1，移动个体密度ρ=0.1，移动个体的速度模v=0.1，个体长程运动的概率pj=0.1.

图5给出了感染半径对系统中感染密度的影响，其中纵轴代表了感染个体的密度，横轴代表了迭代时间步(可代表任意时间单位).从图5中可以清楚地看出，感染的个体数最终趋于0，所有的个体都会进入到无病的状态(R，V)，但是在图5(a)中可以看出，在控制半径相同的情况下，当感染半径较小时(如r1=1或r1=2)，感染个体的密度从初始密度直接下降，而当感染半径r1=3时，随着时间的推移，感染密度会先增加，然后逐渐缓慢下降，说明疾病在人群中大规模流行开来.当控制半径r2越大即接种疫苗的范围越大，则疾病会更快被抑制住，患病的人数也会更少.

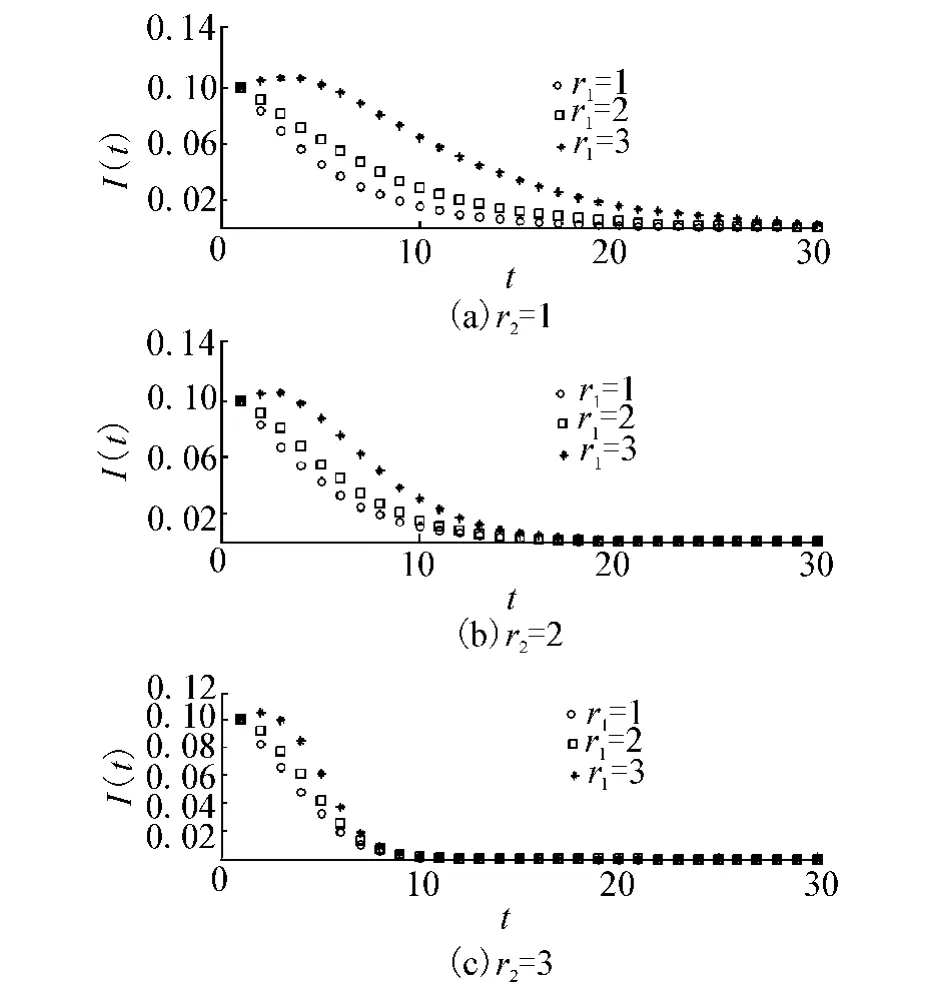
图5 感染半径对感染密度的影响Fig.5 Influence of infection radius on infective density

图6给出了控制半径r2对感染密度的影响.在感染半径(如r1分别为1和2时)较小的情况下，即使控制半径r2设为1时，感染密度也会从初始感染密度直接下降，代表疾病不会大规模流行开来.当感染半径(如r1分别为3时)较大的情况下，即使控制半径r2设为3时，感染密度也会从初始感染密度先增加，然后再缓慢下降到0，即疾病在人群中大规模流行开来.总之，从图6(a)～(c)可以看出，感染半径越大即疾病的传染范围越大则疾病在人群中的传播时间越长，患病的人数也会越大.此外，图6(c)图可以看出，当感染半径较大(即疾病的感染范围比较大)时，即使大范围的接种疫苗疫情也不会得到控制，这就提示人们在面临较高感染风险时，对高传染性个体进行隔离和控制，限制其运动，减小其感染范围(半径)是降低其大规模传播的一个有效手段.

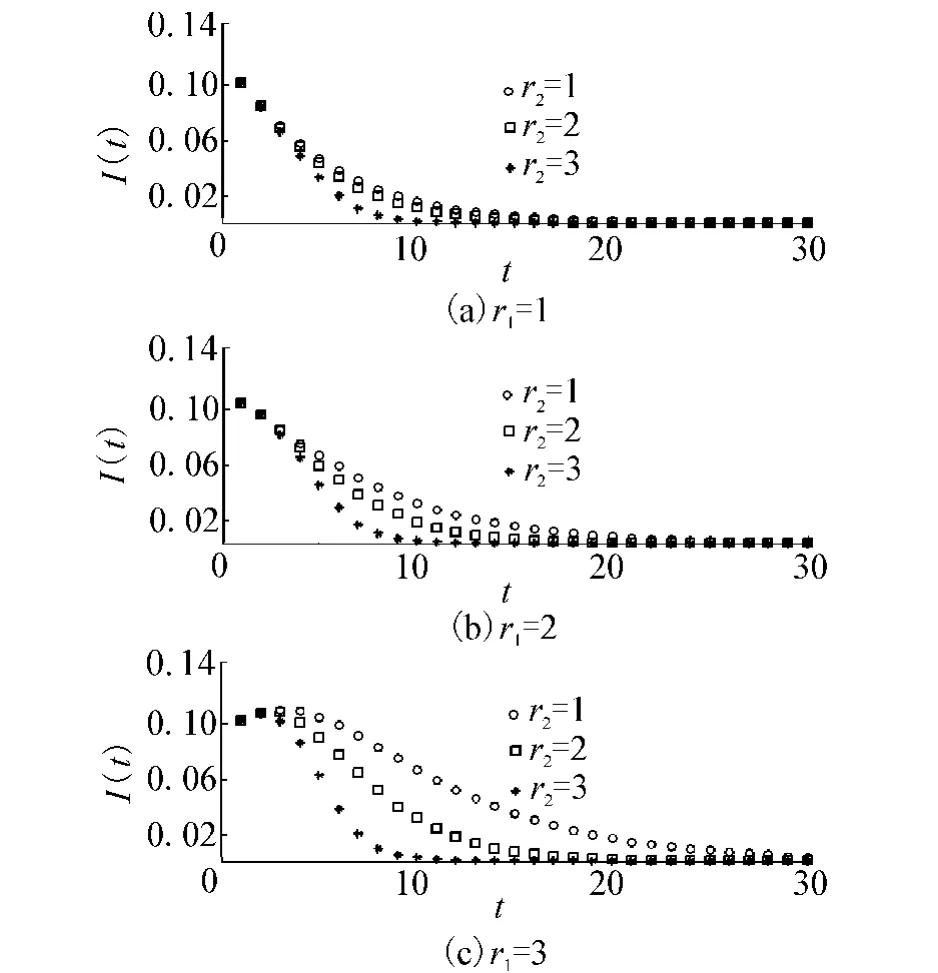
图6 控制半径对感染密度的影响Fig.6 Influence of control radius on infective density

图7表明了移动个体密度对感染个体变化曲线的影响.在图7中，模型参数与图5和6中设置基本相同，只是感染半径和接种半径均都设为2，即r1=r2=2.‘o’、‘□’、‘+’、‘＊—’4 条曲线分别代表了移动个体密度ρ为0.1、0.2、0.3、0.5的时候感染人群变化曲线，当ρ=0.1时，感染密度从0.1开始逐渐下降到0，疾病没有流行开来;当ρ=0.2，0.3，0.5时，随着移动个体密度不断加大，感染密度从初值0.1开始先是增加，到达一个峰值后逐渐减小，最终趋于0，代表了疾病在人群中大规模的扩散.这也提示了在面临传染病爆发时，要对人群进行疏散，降低人群密度，从而到达抑制疾病大规模的传播.

在图8中，给出了个体移动方向对感染密度的影响.同样，个体总数N=10 000，感染半径和接种半径均为2，即r1=r2=2，其他参数设置与前面保持一致.只是未感染者(包括S和R状态的个体)按照图2中所示的“趋利避害”性限制其运动方向，即当一个未感染者(S，R)的一定范围内(例如r1=2)有感染者I，那么这个未感染者会背离感染者的方向(α=180°)移动.在图8中，实线和虚线分别代表了没有控制个体移动方向(α=360°)和控制个体移动方向(α=180°)2种情况下的感染个体密度的变化情况.从图8中可以看到，虚线比实线更快地下降到0，是因为当未感染者背离感染者的时候，相当于减小了个体被感染的风险，缩短了疾病传播的时间，这与人们的基本认识是一致的.

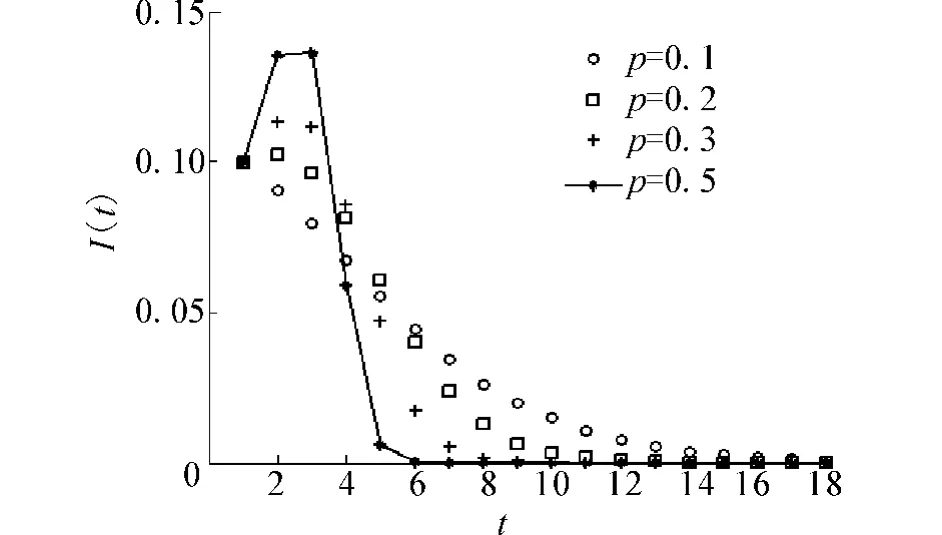
图7 移动个体密度对感染人群的影响Fig.7 Influence of the density of mobile individuals on infective population

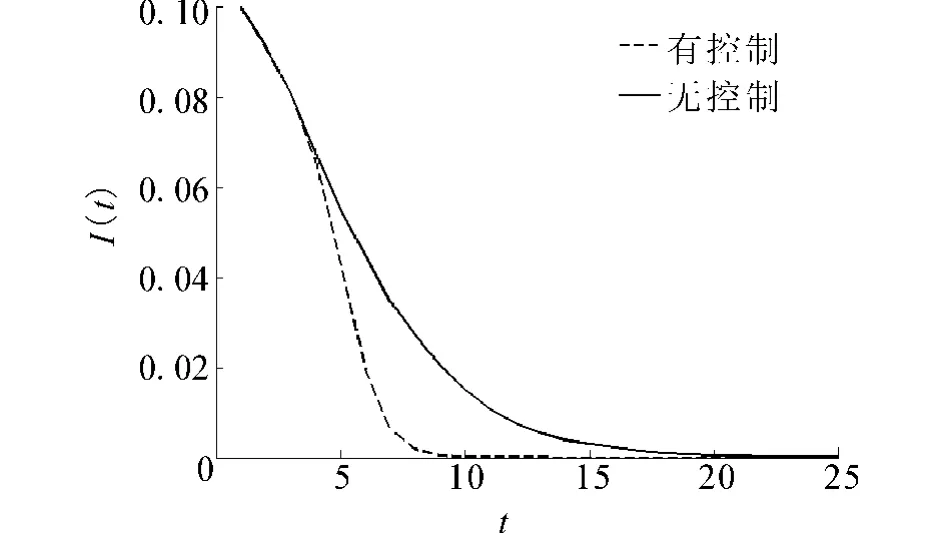
图8 个体移动方向对感染群体的影响Fig.8 Influence of the direction of individual motion on infective population

4 结束语

传染病动力学是对真实传染病进行建模、预测和控制的有效理论和方法，在传染性疾病传播规律和预防接种等方面有着成功的应用，本文将个体运动和局部状态与SIR模型结合，提出了改进的SIR疾病传播模型，研究了局域控制对流行疾病传播的影响.每种疾病的感染范围不同，在模型中体现为r1不同，选择接种疫苗的人群范围不同在模型中体现在r2不同，在一定的条件下讨论了r1和r2分别对整体疾病传播的影响.结果显示当疾病的感染范围较小时，只要进行小范围的接种疫苗或控制其随机运动时，即可实现有效的控制;对于感染范围较大即感染力强的疾病，必须采取大范围的接种才能有效地抑制疾病的传播，减少被感染的人数.这就提示人们，在现实生活中，为了较快地抑制疾病的传播，可以采取隔离具有高传染性的个体，限制其运动范围，减小其感染范围的措施.在接种疫苗的时候可以根据疾病感染范围的大小，权衡接种疫苗范围和数量，减小控制疾病传播的成本.

此外，还分析了个体在二维平面空间中只限制染病个体的运动，使其只做局部运动，而其他个体执行完全随机运动时，和限制染病个体方向的时候疾病传播程度，实验结果表明了限制个体移动的方向可以更快抑制疾病的传播.

［1］DYE C，GAY N.Modeling the SARS epidemic［J］.Science，2003，300(5627):1884－1885.

［2］SMALL M，WALKER D M，TSE C K.Scale－free distribution of avian influenza outbreaks［J］.Physical Review Letters，2007，99(18):188702.

［3］FRASER C，DONNELLY C A，CAUCHEMEZ S，et al.Pandemic potential of a strain of influenza A(H1N1):early findings［J］.Science，2009，324(5934):1557－1561.

［4］马知恩，周义仓，王稳地，靳帧.传染病动力学的数学建模与研究［M］.北京:科学出版社，2004:23－28.

［5］陈关荣.复杂网络及其新近研究进展简介［J］.力学进展，2008，38(6):653－662.

CHEN Guanrong.Introduction to complex networks and their recentadvances［J］.Advances in Mechanics，2008，38(6):653－662.

［6］李翔.复杂动态网络传播动力学［J］.力学进展，2008，38(6):723－732.

LI Xiang.Spreading dynamics on complex dynamical networks［J］.Advances in Mechanics，2008，38(6):723－732.

［7］夏承遗，刘忠信，陈增强，袁著祉.复杂网络上的传播动力学及其新进展［J］.智能系统学报，2009，4(5):392－397.

XIA Chengyi，LIU Zhongxin，CHEN Zengqiang，YUAN Zhuzhi.Transmission dynamics in complex networks［J］.CAAI Transactions on Intelligent Systems，2009，4(5):392－397.

［8］PASTOR－SATORRAS R，VESPIGNANI A.Epidemic spreading in scale－free networks［J］.Physical Review Letters，2001，86(14):3200－3203.

［9］SHI H J，DUAN Z S，CHEN G R.An SIS model with infective medium on complex network［J］.Physica A，2008，387:2133－2144.

［10］LIU Z H，HU B.Epidemic spreading in community networks［J］.Euro－physics Letters，2005，72(2):315－321.

［11］XU X J，ZHANG X，MENDES J F F.Impacts of preference and geography on epidemic spreading［J］.Physical Review E，2007，76:056109.

［12］HUANG W，LI C G.Epidemic spreading in scale－free networks with community structure［J］.Journal of Statistical Mechanics，2007(1):10－14.

［13］ZHANG H F，SMALL M，FU X C.Different epidemic models on complex networks［J］.Communication of Theoretical Physics，2009，52:180－184.

［14］ZHANG H F，ZHANG J，ZHOU C S，et al.Hub nodes inhibit the outbreak of epidemic under voluntary vaccination［J］.New Journal of Physics，2010，12:023015.

［15］MIRAMONTES O，LUQUE B.Dynamical small－world behavior in an epidemical model of mobile individuals［J］.Physica D，2002，168(2):379－385.

［16］FRASCA M，BUSCARINO A，RIZZO A，et al.Dynamical network model of infective mobile agents［J］.Physical Review E，2006，74:036110.

［17］LI X，CAO L，CAO G.Epidemic prevalence on random mobile dynamical networks:individual heterogeneity and correlation［J］.European Journal of Physics B，2010，75:319－326.

赵敬，女，1986年生，硕士研究生，主要研究方向为复杂网络病毒传播.

方义，男，1988年生，硕士研究生，主要研究方向为复杂网络病毒传播.

夏承遗，男，1976生，副教授，博士，主要研究方向为复杂系统与复杂网络建模分析、传播动力学等.目前主持国家自然科学基金1项，省部级科研项目1项，其他科技计划项目1项.获天津市科技进步三等奖1项，发表学术论文近20篇，其中被SCI检索7篇.

A susceptible-infected-removed model considering individual mobility and local control

ZHAO Jing1，2，FANG Yi1，2，XIA Chengyi1，2
(1.Tianjin Key Laboratory of Intelligent Computing and Novel Software Technology，Tianjin University of Technology，Tianjin 300384，China;2.Key Laboratory of Computer Vision and Systems(Ministry of Education)，Tianjin University of Technology，Tianjin 300384，China)

In order to effectively analyze and model the spread of infectious diseases，this paper proposed a novel Susceptible－Infected－Removed(SIR)model considering mobile individuals and local control in which the concept of the infection radius and control radius were introduced.Based on the two－dimensional space，the individual motion model and improved SIR model were considered first，and then large－scale numerical simulation was used to explore the influence of the infection radius and control radius on the behavior of disease propagation.At the same time，the paper also investigated the impact of population density and the direction of mobile agents in relation to the spread of disease.Furthermore，some intuitive control strategies were presented to inhibit the diffusion of epidemics on the basis of the proposed novel SIR model;for instance，separating and controlling the infective individual and evacuating high－density populations.

individual motion;SIR model;infection radius;control radius

TP18;O231.5

A

1673－4785(2011)06－0515－05

10.3969/j.issn.1673－4785.2011.06.006

2011－09－01.

国家自然科学基金资助项目(60904063);天津市应用基础及前沿技术研究计划资助项目(11JCYBJC06600);天津市高等学校科技发展基金资助项目(20090813);国家大学生创新实验计划资助项目(101006019).

夏承遗.E－mail:xialooking@163.com.