电池系统对风电并网引起的频率波动控制应用
2011-08-16刘忠仁刘觉民邹贤求吕立召祖映翔
刘忠仁,刘觉民,邹贤求,吕立召,祖映翔
(湖南大学电气与信息工程学院,长沙 410082)
近年来,由于石化资源的日益减少,利用风能、太阳能等可再生能源的分布式发电逐渐兴起,以应对常规能源的枯竭和产生的环境问题。其中风力发电在新型能源中技术最成熟、成本最低、发展最为迅速[1]。
风力发电具有不稳定性,不能保证持续的发电供给[2]。风力发电的能量源--风,是一种自然资源,在很大程度上依赖于天气、地理以及其他因素,且风力发电还具有波动性。因此,大规模风力发电并入电力系统会造成电网频率波动等多方面的影响[3~5]。对于小幅度的频率波动,依靠传统的水力发电和火力发电可以进行很好的频率控制。然而,大型风电场并入电网是未来能源规划的发展趋势[6],因风电场的不稳定性,很可能出现停机脱网,重新启动并网的情况,当大型风电场开启并注入电网时,如果负荷频率控制 LFC(load frequency control)的容量不够,单依靠常规电厂很难进行有效的频率控制。因此,储能系统如NAS电池系统[7]等被推荐用来参与系统频率的控制。
电池系统的引入,可以作为电力系统频率调节所需的容量储能设备,特别是在风电场脱网或并网时,电池系统可通过其充放电功能来平衡电力系统的发电供给和负荷需求,并控制互联电力系统之间的大幅度潮流传输,参与系统的频率调节,抑制频率的大幅波动。
文中通过Matlab/Simulink建模,对互联电力系统的频率控制进行了分析,给出了系统各控制模块的模型,在大型风电场注入电力系统的情况下(平抑风电场脱网与并网对电力系统产生的影响所需要的调节容量基本相同,所以只需讨论一种情况),对含电池储能系统和不含电池储能系统的频率控制进行对比,并分析了电池系统容量对频率控制的影响。
1 系统分析模型
本文建立了两区互连电力系统仿真模型。如图1所示,电力系统区域1和2是通过联络线相互连接,并假定风电机组和电池系统安装在区域2。电池系统作为储能设备参与互联电力系统频率的调节。本系统包含了常规发电频率调节模型,LFC模型,风电场模型和电池系统模型。

图1 两区互联电力系统分析模型Fig.1 Interconnected 2-area power system analyzing mode
图中:M1,M2为发电机组的惯性常数,D1,D2为负荷阻尼常数,LFC为负荷频率控制,ΔPth为火电机组频率调节输出系数,ΔPhy为水电机组频率调节输出系数为联络线功率调节系数。
1.1 频率调节原理
电力系统功率平衡是一个供需随时平衡的动态过程。当系统频率波动时,同步发电机组通过调节器调节原动机输入功率,使发电机组输出功率与负荷需求平衡。在电力系统中,同步发电机转速偏差Δω和系统频率偏差Δf呈线性关系,由发电机组输出的机械功率ΔPm和电磁功率ΔPe的关系式可表示为
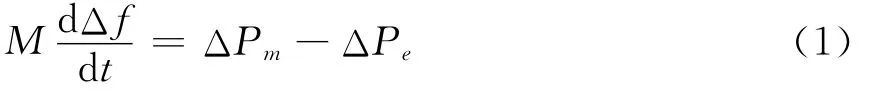
式中:M为系统惯性常数。
在分析负荷频率控制特性时,考虑的是系统中所有发电机的整体特性,策略上假设所有发电机对系统负荷变化的同调响应,并将其等效为一台发电机,等效发电机的惯性常数Meq等于所有发电机组的惯性常数之和,直接由所有的原动机输出机械功率控制其变化。本文参考了文献[8]的频率特性控制模型,可得出如图2所示的频率调节图,传递函数中D为负荷阻尼常数。
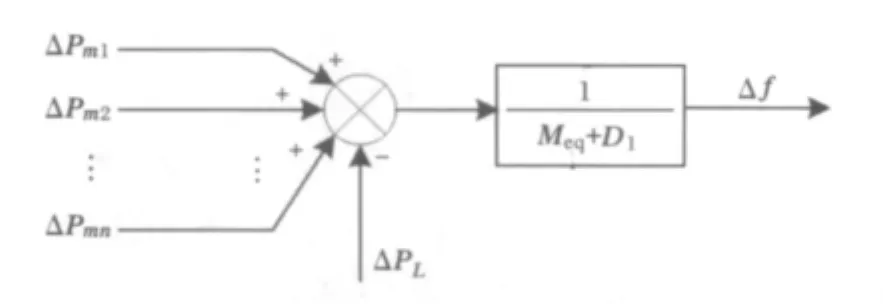
图2 系统频率偏差与功率关系图Fig.2 Diagram of relationship between system frequency deviations and power
1.2 联络线功率调节原理
在有关互联系统联络线潮流控制中,根据文献[9]的直流潮流法,可得到联络线有功功率潮流P12表达式为

式中:XT为线路间的电抗;δ1,δ2为各自线路终端的相角。
假定线路间的功率潮流从区域1流向区域2,并因电机转速偏差Δω和系统频率偏差Δf呈线性关系,且假设Δω=kΔf。则相应额定功率的有关功率偏差ΔP12可表示为
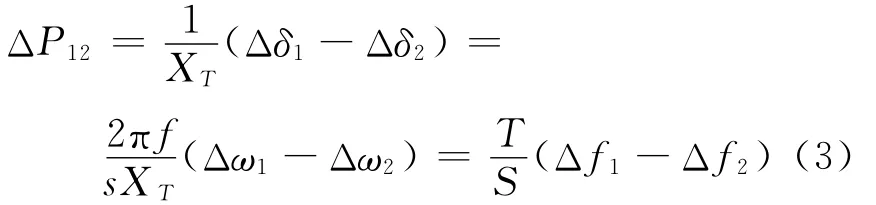
1.3 常规发电机组频率调节模型
当系统频率波动时,会引起各常规机组控制系统调速器调节原动机输入功率,控制各常规机组的输出功率,使发电机组输出功率与系统负荷重新达到平衡,从而使系统频率维持稳定。本文建立的火电机组和水电机组调节模型如图3和4所示。

图3 火电机组频率调节模型Fig.3 Governor control system for thermal unit
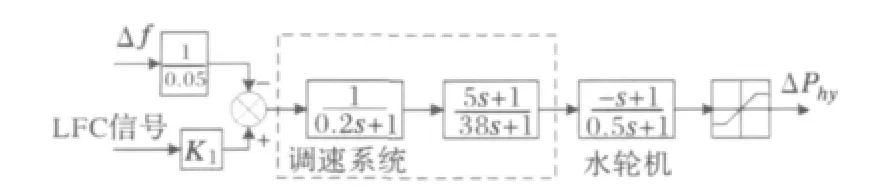
图4 水电机组频率调节模型Fig.4 Governor control system for hydro unit
1.4 LFC模型
在控制区域中,LFC的基本构建信号为负荷调度中心所测量的系统频率和系统区域互联的潮流功率,经过其控制系统处理,使发电机组调节系统等作出相应的响应来调整其输出。本文的LFC模型如图5所示。
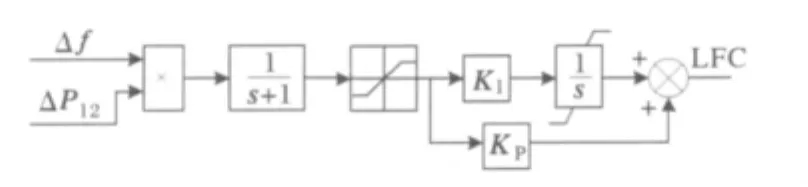
图5 LFC模型Fig.5 LFC model
1.5 风电场模型
因为风电场的输出功率与风速的三次方成正比,所以本文运用文献[10]中的风速模型,对模型参数进行修改,得出了风电场输出功率如图6所示。风力发电机组的启动设为电动机启动,所以开始启动时呈现输出功率为负,即电力系统向风电机组提供功率启动。随着风速的增加,风电机组进入正常运行状态。
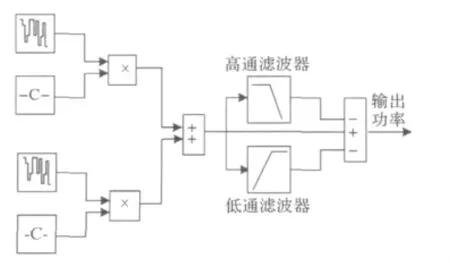
图6 风电场模型Fig.6 Wind power plant model
1.6 电池系统模型
本文中的电池系统引入了NAS电池[10],其特点为能够储存大容量电能并能够分散的安装在电力系统中,可以快速高效的充电并且在一般情况下不会自放电。它能够在紧急情况下迅速灵活的向系统补偿所需的有功功率。此外,该电池比以往的更加高效和耐用。为了能很好的保护电池系统,文中参考了文献[11]的传递函数模型,把电池系统的储存容量和输出功率设置了上下限,其初始容量设置为其额定容量的一半,并假设其在理想情况下进行工作。本文所应用的电池系统模型如图7所示。
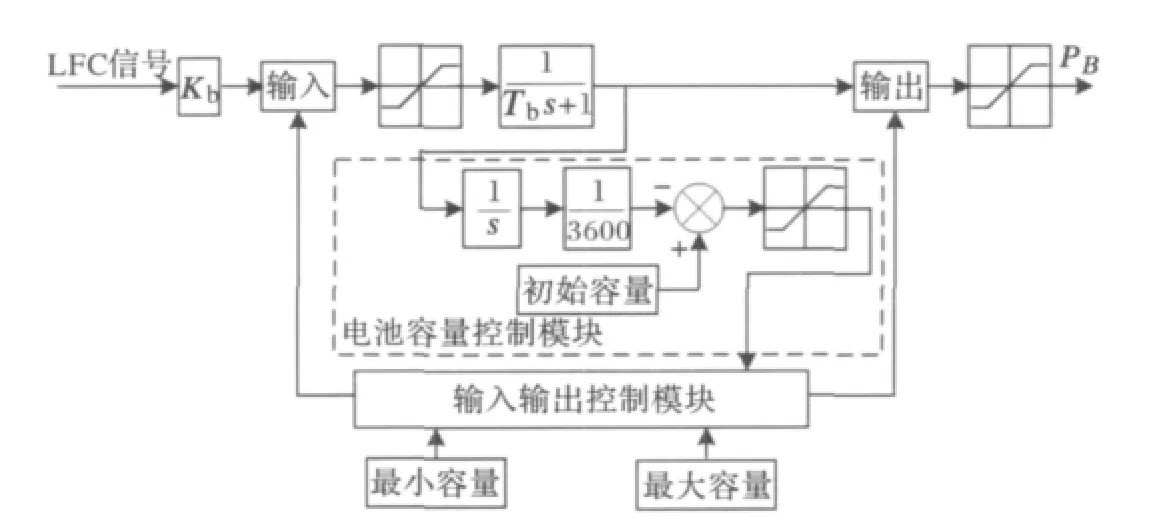
图7 电池系统模型Fig.7 Battery system model
2 仿真分析
通过Matlab/Simulink建立两区互联电力系统模型,系统中区域1和区域2各机组容量和负荷如表1所示。
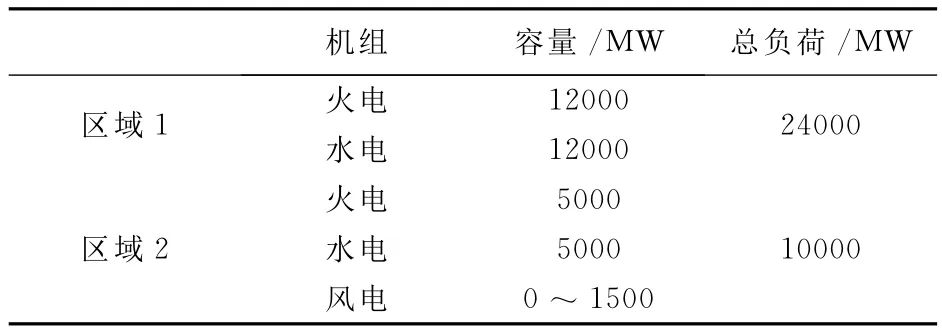
表1 系统容量参数Tab.1 System capacity
利用上述风电场模型,得到了如图8所示的风力发电的输出功率图,其最大的输出功率约为1430MW。
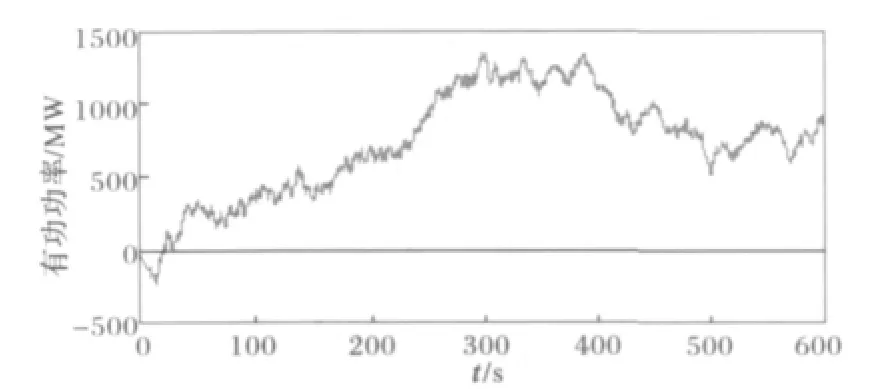
图8 风电场输出功率图Fig.8 Output of wind tubine power
2.1 电池系统及其容量大小对频率控制的影响
本文中,考虑了并入风电场时不含电池系统和包含电池系统对频率控制的影响,并设采用电池系统的储存容量和输出功率分别为(80MWh,300 MW)和(130MWh,500MW)。当如图8所示风电场并入电力系统时,在区域2中,系统频率偏差振荡如图9所示,当不含电池系统时,其最大频率偏差为0.26Hz,而当包含电池系统时,特别当其是大容量电池系统时,其频率偏差明显减少,如当电池容量为(130MWh,500MW)时,其最大频率偏差为0.15Hz。在区域1中,其系统频率偏差如图10所示,区域1只受联络线传输功率引起的频率波动,因风电场引起的功率不平衡在区域2已有部分被同调吸收,且联络线上的传输功率已大幅小于风电场引入的功率,其频率偏差明显小于含风电场的区域2,同样当其电池系统容量增大时,其频率偏差更是明显减少。而区域之间线路的有功潮流如图11所示,也因电池系统特别是当其容量逐步加大时,其功率传输得到明显控制。随着系统频率偏差增大时,其线路间的功率传输也明显加剧。
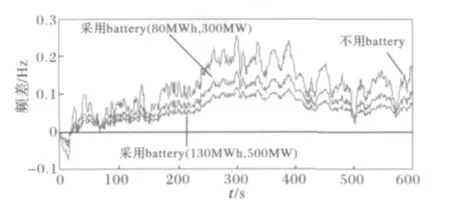
图9 区域2系统频率偏差图Fig.9 Fluctuation of system frequency deviation for area two
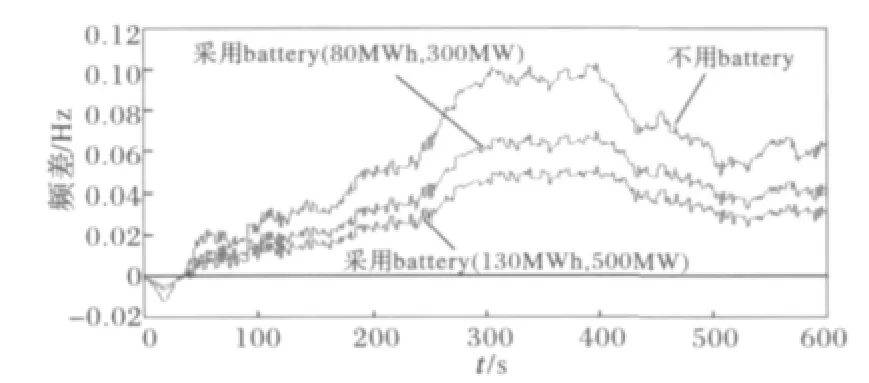
图10 区域1系统频率偏差图Fig.10 Fluctuation of system frequency deviation for area one
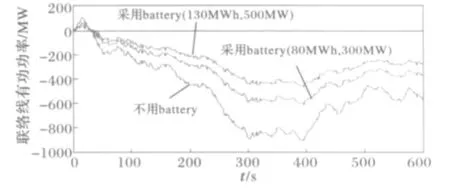
图11 互联线路功率潮流Fig.11 Tie line power flow
2.2 电池系统极限容量的影响
当电池系统容量设置为(90MWh,1200MW)时,其累积的能量如图12所示,当达到时间t=530 s时,其储存的能量达到极限,不能继续充电储能,而此时的输出功率则从约-790MW突变为零,如图13所示,并将对系统频率和互联线路间的功率传输产生剧烈的影响。因此,将电池系统储能应控制在其额定容量范围内。
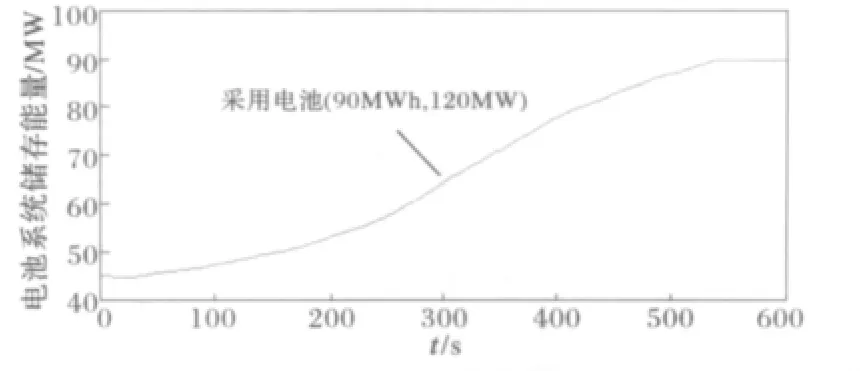
图12 电池储存能量图Fig.12 Diagram for energy stored in battery
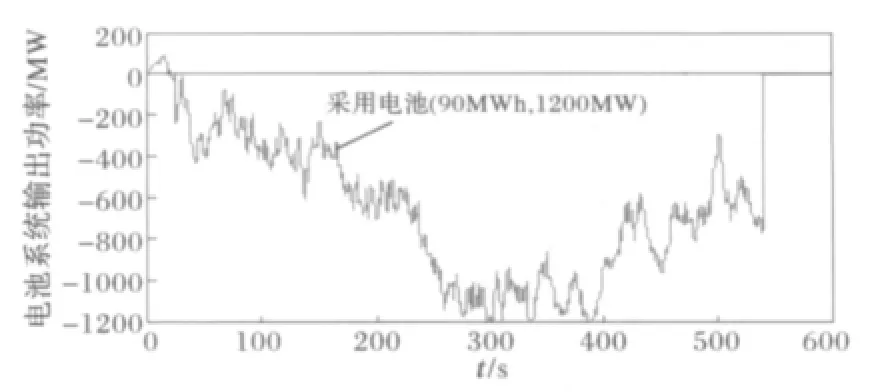
图13 电池系统输出功率图Fig.13 Diagram for fluctuation of battery output
3 结语
本文在大型风力发电场并入电网的情况下,通过Matlab/Simulink仿真建模,分析了电池系统及其容量大小对电网频率控制的影响。通过互联线路功率模型,与不包含电池系统的模型进行对比,很好地验证了电池系统特别是当其容量逐步加大时,对抑制大量风电注入引起的频率波动的有效性,提高了电力系统的稳定性。同时验证了电池系统储能须控制在额定范围内,才能持续有效地参与互联电力系统频率的控制,因此需要根据实际应用情况来选取电池系统容量的大小。
[1]张节潭,程浩忠,黄微,等(Zhang Jietan,Cheng Haozhong,Huang Wei,et al).含风电场的电源规划综述(Review of generation expansion planning for power system with wind farms)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(2):35-41.
[2]雷亚洲(Lei Yazhou).与风电并网相关的研究课题(Studies on wind farm integration into power system)[J].电力系统自动化(Automation of Electric Power Systems),2003,27(8):84-89.
[3]郑太一,严干贵,周志强,等 (Zheng Taiyi,Yan Gangui,Zhou Zhiqiang,et al).电网电压跌落时风电机组运行仿真与实证分析(Simulation and verification of DFIG wind turbine to grid voltage sags)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(3):90-96,120.
[4]石立宝,戴世强,徐政,等(Shi Libao,Dai Shiqiang,Xu Zheng,et al).大规模双馈型风电场并网的系统暂态稳定仿真(Transient stability simulation with large scale grid-connected wind farms DFIG type)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(4):1-7.
[5]潘艳芳(Pan Yanfang).电压不平衡与风电厂运行之间相互影响的研究(Analysis of the interaction between voltage unbalance and wind power plant opera-tion)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2002,14(4):58-60,71.
[6]杨娜,张焰(Yang Na,Zhang Yan).大型风电场并网运行系统暂态稳定性分析(Power system transient stability analysis with large scale wind power integration)[J].水电能源科学(Water Resources and Power),2008,26(2):192-194,174.
[7]Watanabe Shogo,Horiuchi Satoshi,Iwamoto Shinichi.NAS battery system application for frequency ATC improvement [C]//IEEE Power and Energy Society General Meeting,Pittsburgh,USA:2008.
[8]刘梦欣,王杰,陈陈(Liu Mengxin,Wang Jie,Chen Chen).电力系统频率控制理论与发展(Theory and development of power system frequency control)[J].电工技术学报(Transactions of China Electrotechnical Society),2007,22(11):135-145.
[9]刘科研,盛万兴,李运华(Liu Keyan,Sheng Wanxing,Li Yunhua).互联电网的直流最优潮流分解算法研究(Research on decomposition algorithm of DC optimal power flow in large scale interconnection power grids)[J].中国电机工程学报(Proceeding of the CSEE),2006,26(12):21-25.
[10]Michiqami T,Ishii T.Construction of fluctuation load model and dynamic simulation with LFC control of DC power system and frequency converter interconnection[C]//IEEE Power Engineering Society Transmission and Distribution Conference,Yokahama,Japan:2002.
[11]Sasaki Tetsuo,Kadoya Toshihisa,Enomoto Kazuhiro.Study on load frequency control using redox flow batteries[J].IEEE Trans on Power Systems,2004,19(1):660-667.
