配电网单相接地故障信号形态学消噪方法＊

孔 红，郭 倩，张 巍

(1.山西工程职业技术学院机电工程系，太原 030009;2.燕山大学电气工程学院，秦皇岛 066004;3.鞍山电视台，鞍山 114001)

配电网发生单相接地故障时，通常利用零序电流稳态量和暂态量特征进行选线。因单相接地故障信号非常微弱，现场噪声干扰对其影响较大，若对信号不加处理而直接施加选线算法，可能会将噪声作为信号突变点，造成误判。因此进行有效消噪是配电网单相接地故障选线的关键技术之一［1～3］。

数学形态学消噪滤波器与传统数字滤波器相比，解决了数字滤波器存在时滞、非线性相移以及噪声信号频谱重叠不能有效分离的问题，同时还具有算法简便易行、物理意义明确等优点，因此该滤波方法已在图像处理、模式识别、视觉检测等方面得到应用［4，5］。近年来，数学形态学逐步应用到电力系统中，主要涉及到电能质量［6］、变压器励磁涌流的识别［7］、超高速暂态线路保护［8，9］、继电保护［10］等方面。

1 数学形态学滤波器

数学形态学(mathematical morphology)是建立在积分几何和随机集论等数学理论基础上的一门联系实际的科学［11～13］，由法国人 G.Matheron和J.Serra于20世纪60年代提出。它通过一个称作结构元素的“探针”在输入序列中不断移动，提取有用信息，把复杂信号分解为具有物理意义并与背景剥离的各部分。数学形态学最基本的二值形态变换包括膨胀和腐蚀。设输入序列f(n)和结构元素g(n)分别为定义在F={0，1，…，N－1}和G={0，1，…，M －1}上的离散函数，且N≥M。则f(n)关于g(n)的膨胀和腐蚀分别定义为

其中，n=1，2，…，N － 1。

由这两种基本运算引出的还有开、闭运算，f(n)关于g(n)的开、闭运算分别定义为

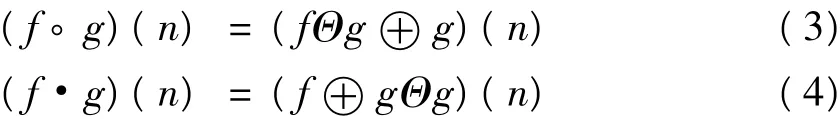
2 组合滤波器的设计

2.1 形态滤波器组合算法

对于一维信号来说，开运算主要是平滑并抑制信号峰值噪声，闭运算平滑并抑制谷底噪声，开闭运算的互联可以组成开-闭(OC)和闭-开(CO)滤波器，可同时抑制正负脉冲噪声，定义如下:

形态开-闭和闭-开滤波器虽然可同时滤除信号的正负脉冲噪声，但存在统计偏倚现象。这是由于开运算的收缩性导致开 －闭滤波器的输出幅度较小，闭运算的扩张性导致闭 －开滤波器的输出幅值较大。统计偏倚现象直接影响到形态滤波器的噪声抑制性能。为消除这个缺点，本文采用OC滤波器和CO滤波器的组合，使处理结果更接近原始信号。设输入信号f(n)由原始信号x(n)和噪声信号s(n)组成，即

则OC滤波器和CO滤波器的组合算法为

2.2 结构元素的选择

除变换形式外，形态滤波输出主要取决于结构元素的形状和长度，通常只有与内核尺寸和形状相匹配的信号才能被保留。形态滤波器结构主要有余弦、矩形、扁平、斜线、半圆、三角结构等。比较可知，对于波形较稳定的正弦信号，用正弦结构元素和半圆结构元素消噪效果较好，但对于含有丰富的暂态成分的信号，则扁平结构元素的综合消噪更好。考虑配电网单相接地信号的特点及算法的简单性，本文采用扁平结构元素进行单相接地故障信号消噪，可在保持信号形状前提下最大限度消噪。

扁平结构元素的形状仅由其宽度决定，而不受其幅值影响，只需确定扁平结构元素宽度对滤波的影响。这里采用均方根误差检验滤波效果，令输入信号为f(n)，输出为y(n)，均方根误差定义为

对于选线算法，信号采样率取每周期64点较合适。图1给出信号采样率为每周波64点情况下滤波信号均方误差与扁平结构元素宽度的关系曲线。其中P为结构元素宽度，E为均方误差。可看出随扁平结构元素长度的增加，E先减小后增加，当扁平结构元素长度在24附近时滤波效果较好。

图1 扁平结构元素宽度的滤波误差曲线Fig.1 Error curves of filtering with pavement width of sturcture element

2.3 滤波算法实现流程

形态滤波器的结构元素取为扁平结构元素，宽度为24。扁平结构元素的幅值对滤波效果不敏感，可取为 1，即 g(m)= ［1，1，…，1］，(m=0，…，23)。现场模拟信号输入选线装置后，首先进行波形采样和A/D转换，得到信号的采样序列f(n)，信号采样率取64点/周波。第二步对采样信号序列进行数学形态滤波，即将结构元素g(m)=［1，1，…，1］序列与信号序列f(n)按本文方法进行形态学滤波，得到滤波后信号y(n)，如式(8)。滤波后信号即可应用于选线算法中。滤波算法流程见图2。

图2 数学形态学滤波算法流程Fig.2 Flowchart of mathematical morphology filtering algorithm

3 仿真算例

仿真系统结构如图3所示。线路正序参数为:R1=0.17 Ω/km，L1=1.21 mH/km，C1=70.6 pF/km;线路零序参数为 R0=0.23 Ω/km，L0=2.175 mH/km，C0=22.5 pF/km;线路长度为 L1=5 km，L2=10 km，L3=15 km，L4=18 km，L5=24 km，消弧线圈按10% 过补偿。

图3 模型结构原理图Fig.3 Diagram of the simulated network

仿真结果如图4～7所示。

图4给出中性点不接地方式下故障线路5和非故障线路1叠加随机噪声后的零序电流仿真波形。图5为中性点经消弧线圈接地方式故障线路5零序电流仿真波形。

为对比分析，选择余弦结构元素和扁平结构元素对叠加随机噪声的零序电流进行滤波效果比较。经多次仿真分析，可知余弦结构元素幅值一般取暂态零序电流幅值的1/30较合适。这里余弦结构元素取 x=－π/2∶0.02∶π/2，g1=2×cos(x)，其宽度为16、幅值为2。而扁平结构元素按2.3所述，其幅值取为1，宽度为24，则g2= ［1，1，…，1］。信号采样率为64点/周波。图6和图7分别给出应用这两种结构元素对图4和图5中线路零序电流波形进行滤波消噪的处理结果。

从图6和图7可知，余弦结构元素的平滑能力很强，去噪声效果最明显。但余弦结构对于暂态信息部分进行了过度平滑，容易使暂态波形产生失真。而扁平结构元素能在保留故障信号特征的前提下最大限度地抑制噪声干扰，且扁平结构元素的自适应性很好。

图7 扁平结构元素消噪结果Fig.7 De-noising result with pavement structure

4 结语

针对配电网单机接地故障信号的特点，本文研究基于应用数学形态学的单相接地故障信号消噪法，采用扁平结构元素和组合滤波算法实现了单相接地故障信号的有效消噪。选用扁平结构元素能有效抑制噪声干扰，有利于提高单相接地故障选线的准确性。

［1］Gargoom Ameen M，Ertugrul Nesimi，Soong Wen L.Investigation of effective of automatic recognition systems of power－ quality events［J］.IEEE Trans on Power Delivery，2007，22(4):2319 －2326.

［2］Panigrahi B K，Sinha S K.Detection and classification of non－stationary power disturbances in noisy conditions［C］∥International Conference on Power Electronics，Drives and Energy Systems，New Delhi，India:2006.

［3］Panigrahi B K，Mishra S.Intelligent classification of power quality disturbances in a distribution network［C］∥IEEE Region 10 Annual Conference，Melbourne，Australia:2005.

［4］Maragos P.Differential morphology:multiscale image dynamics，max-min difference equations， and slope transforms［C］∥IEEE International Conference on Image Processing，Austin，USA:1994.

［5］李向吉，丁润涛(Li Xiangji，Ding Runtao).脉冲噪声污染图像中的数学形态边缘检测器(Mathematical morphological edge detectors for noisy images corrupted by impulses)［J］.中国图像图形学报(Journal of Image and Graphics)，1998，3(11):903－906.

［6］束洪春，王晶，陈学允(Shu Hongchun，Wang Jing，Chen Xueyun).动态电能质量扰动的多刻度形态学分析(Multiscale morphology analysis of dynamic power quality disturbances)［J］.中国电机工程学报(Proceedings of the CSEE)，2004，24(4):63－67.

［7］郑涛，刘万顺，肖仕武，等(Zheng Tao，Liu Wanshun，Xiao Shiwu，et al).一种基于数学形态学提取电流波形特征的变压器保护新原理(A new algorithm based on the mathematical morphology for power transformer protection)［J］.中国电机工程学报(Proceedings of the CSEE)，2004，24(7):18－24.

［8］林湘宁，刘沛，高艳(Lin Xiangning，Liu Pei，Gao Yan).基于故障暂态和数学形态学的超高速线路方向保护(ltral-high-speed line directional protection based on transient and mathematical morphology)［J］.中国电机工程学报(Proceedings of the CSEE)，2005，25(4):13－18.

［9］Wu Q H，Zhang J F，Zhang D J.Ultra-high-speed directional protection of transmission lines using mathematical morphology［J］.IEEE Trans on Power Delivery，2003，18(4):1127－1133.

［10］邹力，刘沛，赵青春(Zou Li，Liu Pei，Zhao Qingchun).级联形态梯度变换及其在继电保护中的应用(Series multi-resolution morphological gradient and application in protection relaying)［J］.中国电机工程学报(Proceedings of the CSEE)，2004，24(12):113 －118.

［11］石佳，黄纯，李扬(Shi Jia，Huang Chun，Li Yang).一种基于数学形态学的扰动信号分形检测方法(A fractal detection method based on mathematical mor-phology for disturbance signal)［J］.电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2008，20(5):86－90.

［12］赵春晖.数字形态滤波器理论及其算法研究［M］.北京:高等教育出版社，2002.

［13］崔屹.图像处理与分析-数学形态学方法及应用［M］.北京:科学出版社，2000.