利用行波经验模态分解实现线路故障测距＊

徐伟宗，唐昆明，2

(1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044;2.重庆新世纪电气有限公司，重庆 400030)

基于行波原理的线路故障测距具有精度高、受系统运行方式小等优点［1］，而影响行波测距准确性的两大因素，即波头识别及波速的确定一直是行波测距的最主要难点。利用小波的奇异性检测理论来实现行波波头的识别以及通过小波分析尺度来确定行波的中心频率，从而最终确定行波速度是现在比较通用的一种做法，但在使用小波变换法时，对小波基以及尺度的选择提出了较高的要求。

输电线路发生故障时产生的行波是一种突变的、具有奇异性的暂态信号，其频谱包含了从低频到高频的一系列成分，称为行波的自然频率［2］，而突变信号在突变点处会表现为频率的急剧变化，这种急剧变化的频率在频谱上体现为高频分量，尤其是能量强、幅值大的高频分量。通常情况下高频信号较低频信号的衰减大，但是其传播速度快，且传播过程中速度趋于稳定［3］，在行波测距的基本原理“时间乘以速度等于距离”中，速度是被当作恒速来处理的，因此，如果能够将这种传播速度稳定的高频分量从行波中提取出来，用来确定行波的时间参数，同时使用该频率下的行波传播速度进行故障测距，从理论上讲应当可以得到比较精确的测距结果。但是由于故障发生的随机性，加之行波在传播过程中发生衰减、频散等原因，要使用常规的频域滤波器来提取行波的某次谐波分量是很困难的。

一种根据信号自身的特征时间尺度来经验地识别信号固有的振荡模式，然后据此来分解信号且具有多分辨率特性和良好自适应性能的信号处理方法—经验模态分解EMD(empirical mode decomposition)，为提取行波的高频分量提供了可能，同时也为实现行波频率与速度的结合提供了一个新方向，ATP仿真表明此方法具有可行性且测距精度好于小波变换。

1 EMD的原理及主要特点

N.E.Huang等人根据瞬时频率的意义，提出了一类被称为本征模函数 IMF［4］(intrinsic mode function)，其定义为:在整个信号中，零点数与极点数相等或至多相差一;在信号上任意一点处，由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值均为零，即要求信号关于时间轴局部对称。

为了将信号分解为IMF，N.E.Huang及其合作者提出了一种新的数据分解方法—经验模态分解方法，它通过不断剔除信号的局部极大值和局部极小值连接的上下包络线的均值而筛选出各个固有模态函数，最后得到原始信号S(t)的分解形式如下，

式中:Ci(t)表示第i个模态函数;rn(t)为残余量，通常表示直流分量，在重构信号时，有时也把残余量剔除掉。经验模态分解的具体步骤已有多篇文献详细描述［4～7］，限于篇幅，本文不再说明，但其过程可以简单地用下图表示为

图1 EMD分解过程Fig.1 Process of empirical mode decomposition

以上所分解出的各 IMF分量，即 C1(t)，C2(t)，C3(t)，…，Cn(t) 是按照频率的高低排列的，通常前几个IMF分量集中了原始信号中的主要信息。由于高频分量往往最能直观而敏感地体现信号的突变信息，因此，根据EMD分解出的各个IMF分量，越靠后的分量在突变点处的突变程度会越弱，所以通常只需选用1～2个IMF分量就已经能够很好地确定突变点的位置了。

经验模态分解EMD的本质是根据信号的特征时间尺度来经验地识别信号固有的振荡模式，然后据此来分解信号，主要具有如下特点:它基于信号自身的特征时间尺度，每个IMF分量都反映了信号不同的尺度，且随信号本身的变化而变化，具有良好的自适应性能，而傅里叶变换、小波变换，从严格意义上说并不具有自适应性［5］;EMD根据信号的局部特征尺度对信号进行筛分，这个过程表现为尺度带通滤波器对信号进行过滤。在一定尺度范围内的信号被分离而形成的IMF分量具有有限带宽的频谱，而突变信号在突变点会表现为频率的急剧变化，根据频率与特征尺度的关系，这种急剧变化的频率反映在时域上是特征尺度的显著变化，因此，基于时间特征尺度的EMD能够有效地分离出信号的突变部分，确定突变点的位置。

信号可能会受到干扰的影响，为了消除干扰信号的影响，一方面，可以直接采用类似小波变换中的硬(或软)门限去噪方法，对每一个IMF成分作门限处理，其实现过程和小波变换方法类似［7］;另一方面，也可以通过提高EMD的分解阶数(特征时间尺度)来实现去除干扰和噪声，即在所分解出的IMF分量中，取靠后的IMF分量，EMD所分解出的IMF分量的频率随着分解阶数的增大而降低，而信号的噪声成分主要分布在高频段，也就是主要集中在前几个分量中，因此取靠后的IMF分量能够消除干扰信号的影响，这也和小波具有类似性，因为小波变换也是通过改变其变换尺度来实现去除干扰信号的影响，EMD中的‘阶数’相当于小波变换中的‘尺度’，所不同的是EMD中的‘阶数’是根据信号本身产生，会随着信号本身的变化而变化，具有良好的自适应性，而小波变换中的‘尺度’是事先设定的，适应性不及EMD。

2 行波的EMD应用

输电线路故障行波的EMD分解及其小波变换应用如图2、图3所示。

图2、图3是在仿真过程中得到的故障行波及EMD(采用端值延拓的边界处理方法)图和小波变换图(小波基函数为db，尺度为4)，A相接地故障，故障距离为距离M端母线处90 km，过渡电阻Rg=100 Ω，故障初相角 φ =60°，线路全长 200 km，采样频率为1 MHz。从图中可以清楚的看到，小波变换的结果是在信号的突变处形成模极大值;而EMD分解的结果是将引起信号突变的高频分量提取了出来，它所起的作用如同一滤波器，但并非是一般意义上的频域滤波，而是以时间特征尺度为特征的时空尺度滤波［7］，这里同时也验证了EMD的第二个特点。比较图2中各突变处的高频分量，可以发现它们之间存在极性差异，从而可以在一定程度上用来识别故障点的反射波和对端母线或相邻母线的反射波，这和小波变换具有类似性，因为小波变换同样是依靠其极性的差别来识别各反射波的;这里有必要指出，上图所分解得出的IMF分量只是前文定义的IMF分量的一种近似图，因为它并没有完全满足IMF所要求的条件，如果再继续分解下去，不仅计算量要加大，而且会弱化高频分量的作用，同时由EMD分解过程所产生的端点效应也会进一步扩大［5］。

图2 故障行波及其EMDFig.2 Fault travelling wave and it＇s EMD

为获得故障距离，这里需要定义行波的时间参数，这里定义高频分量的前半周期的峰值时刻为行波的到来时间，而小波变换同样取其峰值时刻的值，将峰值时刻作为行波的到来时间主要是考虑到该时刻作为峰值时间，特征明显，便于计算。

由图可知，由EMD确定的时间所对应的采样点序列号为:Nm=372，Nn=439，小波确定的时间对应的序列号分别为:Nm=306，Nn=375。根据行波的特点，行波分量的频率越低，其传播速度越慢;行波分量的频率越高，其传播速度也越快，并且越趋于一致(接近光速)，文献［3］给出行波的线模高频分量的传播速度一般是在2.950×105km/s～2.990×105km/s之间，由EMD分解出的分量对应的是行波的高频分量，所以为方便起见，这里假定V=2.990×105km/s，在采样频率已知的情况下，容易求得故障距离为:Lmk=89.9835 km，误差为|ΔL|=0.0165 km(EMD 方法);Lmk=89.6845 km，误差为|ΔL|=0.3155 km(小波变换法)。

图3 故障行波及其小波变换Fig.3 Fault travelling wave and it＇s wavelet transform

可见，由EMD方法得出的故障距离的精度明显要比小波变换高许多，但这是有内在原因的。由EMD分解出的IMF分量对应的是行波的高频分量部分，而行波速度取的又是其高频分量对应下的速度，即基本实现了高频分量对应高频速度，而小波变换并没有这样的对应关系，因此EMD的测距准确性高并不奇怪。实际上，前面所假定的高频分量的波速度只是一经验值，如果能够求出IMF分量所对应的瞬时频率，再根据行波的频率与其传播速度的关系，那么就能得出精确的行波速度，从而进一步提高测距的准确性。从理论上讲，用EMD分解得出的IMF分量，可以通过Hilbert变换求出其各时刻的瞬时频率，文献［8］就是将EMD分解得出的IMF分量通过Hilbert变换，由此得出各瞬时频率，再由瞬时频率来决定行波波头时刻。但是，由于EMD自身的局限性及行波本身的复杂性，用EMD方法所分解出IMF分量通常只是一种IMF的近似图，事实上由图2也可以清楚地看到只有波形的前半部分完全达到了IMF所定义的条件，而后半部分只是基本满足其条件，在这种情况下，如果使用Hilbert变换，那么也只有前半部分的变换结果具有实际上的物理意义，否则，如果使用了伪频率处的时间值将会导致错误的结果。在仿真这种特殊条件下固然容易判断哪部分满足Hilbert变换的条件，但在现场的实际条件下，这是很困难的;另外，使用瞬时频率来确定行波波头时间，由于瞬时频率之间并不存在极性上的差异，因而也难以用来确定各反射波头。因此，本文直接通过IMF分量来决定行波波头时刻值，既避免了上述方法的不足，同时也减少了计算量。

3 ATP仿真实验

为了进一步验证该方法的有效性及在各种故障情况下的测距精度，本文利用电磁暂态程序ATP软件进行了大量的仿真测试，限于篇幅，仅列出部分数据。

图4 ATP仿真模型Fig.4 ATP simulation model

设三相线路为平衡线路，使用双端行波测距原理，采用电流行波，采样频率1 MHz，采用Clarke相模变换矩阵，线路参数选用依频特性模型JMarti，设线路全长200 km，行波速度V=2.990 ×105km/s，仿真实验的部分结果如表1所示。

表1 不同故障点的测距结果和测距误差(AG，Rg=100 Ω，φ =60°)Tab.1 Different fault location results and errors(AG，Rg=100 Ω，φ =60°)

4 仿真结果分析

由表1可知，由EMD方法计算得到的最大相对误差为0.257%，而由小波变换法得到的最大相对误差为0.4148%，应当说两者都达到了比较令人满意的结果。但是，EMD方法计算的准确性明显高于小波法一些，其原因已在前文中说明，此处不再赘述。

由于行波在传播过程中发生衰减，其衰减程度跟行波频率与传播距离密切相关。在使用一般的双端测距(单波速)公式:

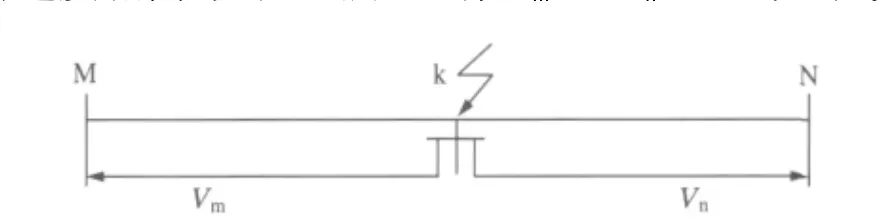
图5 初始行波传播Fig.5 Initial traveling wave transmition

其实是作了假设的，也就是假设行波在向两端传播的速度相同，如图5所示，有Vm=Vn=V。如果故障点处于线路中点或故障点距离两端母线的距离之差不大时，由于两端行波的衰减情况基本相同，因而假设Vm=Vn=V是可行的，所引起的实际误差也并不大，而当故障点到两端母线的距离之差很大时，那么传播到母线两端的行波中的主频分量就会出现较大的差异，这样由EMD所提取的IMF分量的频率应当是不同的，从而两端的波速就不一样，这样一来上述的双端测距公式就会带来较大的误差，表1的结果已经表明存在这样一种趋势。以实际故障距离5 km为例，用EMD方法得到的两端行波时间所对应的采样点序列号分别为Nm=19，Nn=657，在V=2.990 ×105km/s时，得到的故障距离是 Lmk=4.6190 km，误差为 0.3810 km，如果考虑到两端行波的频率分量不一样，应当对波速做一定的修正。由于行波的衰减是以指数规律进行的，因此在对波速进行修正时，可按照指数规律进行，修正的结果是要使故障点靠近母线一侧的波速高于另一侧的波速，如取Vm=2.990×105 km/s，Vn=2.978 ×105 km/s，然后通过下述(双波速)公式:

可以算得故障距离为Lmk=5.0119 km，误差为0.0119 km，可见此时显著提高了测距精度。针对此种情况，可以先用前面的单波速公式，如果算得故障点是处于线路首端及附近或末端及附近，那么再采用双波速公式进行修正，就可得到比较精确的故障点位置。

5 结论

(1)本文利用EMD分解原理所具有良好的时频局部化性能、自适应多分辨特性来提取行波的高频分量，并通过高频分量下的经验波速来计算故障距离，初步实现了行波频率与其速度的结合，ATP仿真表明此方法的计算精度好于小波变换。

(2)行波的高频分量具有传播速度快，且传播过程中速度趋于稳定的特点，EMD的使用为利用行波的高频分量进行故障测距提供了理论基础。

(3)由于行波的速度跟行波分量的频率与线路的结构参数相关，而线路的参数又会受到包括天气、地理位置等众多因素的影响，要精确获取行波速度实属不易，因此通过EMD来提取行波的高频分量，并使用高频分量下的经验波速度来计算故障距离更具有实际工程意义。

［1］葛耀中.新型继电保护与故障测距原理与技术［M］.西安:西安交通大学出版社，1996.

［2］Giovanni Miano.Transmission Lines and Lumped Circuits［M］.San Diego，USA:Academic press，2001.

［3］徐丙垠，李京，陈平，等(Xu Bingyin，Li Jing，Chen Ping，et al).现代行波测距技术及其应用(Modern fault location technique based on fault generated traveling waves and their applications)［J］.电力系统自动化(Automation of Electric Power Systems)，2001，25(23):62－65.

［4］Huang N E，Zheng Shen，Steven R L，et al.The em-pirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of Royal Society London，1998，454:903－995.

［5］钟佑明(Zhong Youming).希尔伯特－黄变换局瞬信号分析理论的研究(Research on the Local－instantaneous Signal Analysis Theory of the Hilbert-Huang Transform)［D］.重庆:重庆大学机械工程学院(Chongqing: College of MechanicalEngineering，Chongqing University) ，2002.

［6］姚林朋，黄成军，钱勇(Yao Linpeng，Huang Chengjun，Qian Yong).基于EMD的局部放电窄带干扰抑制算法(Empirical mode decomposition based DSI suppression algorithm in partial discharge detection)［J］.电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2007，19(5):33 －38.

［7］谭善文，秦树人，汤宝平(Tan Shanwen，Qin Shuren，Tang Baoping).Hilbert-Huang变换的滤波特性及其应用(The filtering character of Hilbert-Huang transform and its application)［J］.重庆大学学报(Journal of Chongqing University)，2004，27(2):9 －12.

［8］张小丽，曾祥君，马洪江，等(Zhang Xiaoli，Zeng Xiangjun，Ma Hongjiang，et al).基于 Hilbert-Huang变换的电网故障行波定位方法(Power grid faults location with traveling wave based on Hilbert-Huang transform)［J］.电力系统自动化(Automation of Electric Power Systems)，2008，32(8):64－68.