电力系统故障诊断的量子粒子群优化算法*
2011-08-16李晓,黄纯
李 晓,黄 纯
(1.湖南大学电气与信息工程学院,长沙 410082;2.株洲职业技术学院,株洲 412000)
随着电网的不断发展和电力走向市场,人们对电网全运行和供电可靠性的要求越来越高;而电力系统故障诊断系统为供电的可靠性和连续性提供了有力的保障。
电力系统故障诊断系统尽可能利用采集信息识别故障元件和误动作的保护与断路器,其中故障元件的识别是关键问题。目前,故障诊断方法有逻辑处理方法、专家系统方法(主要是基于Petri网的专家系统方法)、枚举法、人工神经元网络方法和基于优化技术的方法等。其中基于优化技术的方法又包括遗传算法、混沌算法、模拟退火算法等。
专家系统方法直观,解释能力强,但是难以获取完备的知识库,无学习能力,容错能力较差。枚举法简单,但该方法的指数时间特性使之无法用于大系统的研究。人工神经元网络方法的故障诊断性能取决于样本集是否完备,对于大型的电力系统要形成完备的样本集极其困难,因而其诊断结果的正确性在原理上无法保证。此外,对于不同的故障元件引起相同的保护和断路器动作的情况,这种方法只能给出其中的一个解,局限性较大。一般的模糊系统采用了与专家系统类似的结构,所以它也具有专家系统的一些固有的优缺点,但增加了容错能力。遗传算法GA(genetic algorithm)从优化的角度出发基本上可解决故障诊断问题,尤其是在复杂故障或存在保护、断路器误动作的情况下,能够给出全局最优或局部最优的多个可能的诊断结果,但是稳定性差、速度较慢。
粒子群优化算法 PSO(particleswarm optimization)是优化技术的一种,源自对鸟群捕食行为的研究,它本质上是属于迭代的随机搜索算法,具有并行处理特征,鲁棒性好,易于实现,且计算效率较高。但标准粒子群系统中存在一个最大的缺点,那就是粒子的收敛是以轨道的形式实现的,并且粒子的速度总是有限的,因此在搜索过程中粒子的搜索空间是一个有限的区域,不能覆盖整个可行的空间,所以标准PSO算法并不能保证收敛到全局最优解。
2004年,Sun等人从量子力学的角度出发提出了一种新的PSO算法模型[9]。这种模型以DELTA势阱为基础,认为粒子具有量子行为,并根据这种模型提出了基于量子行为的粒子群优化QPSO(quantum-behaved particle swarm optimization)算法。在量子空间中,粒子在整个可行解空间中进行搜索,因而QPSO算法的全局搜索性能远远优于标准PSO算法。
本文应用量子粒子群优化算法来求解电力系统故障诊断的问题。并进行了仿真计算,将其与标准PSO算法和遗传算法进行了比较,发现量子粒子群算法不但可直接求解最小化问题,而且具有收敛速度快、稳定性好的优点。
1 故障诊断的0-1整数规划模型
电力系统故障诊断就是利用保护和断路器的动作信息来推断可能的故障位置,可以表示为使下述目标函数最小化的问题:

式中:nr为保护总数目;nc为断路器总数目;S为一个n维向量,表示系统中元件的状态(n为系统中元件的数目);S中的第i个元素si表示第i个元件的状态,si=0或1分别表示第i个元件的正常或故障状态;rk为一个nr维向量,表示nr个保护的实际状态;R中的第k个元素rk表示第k个保护的实际状态,rk=0或1分别表示第k个保护的未动作或动作状态;(S)为一个nr维向量,表示nr个保护的期望的状态;R*(S)中的第k个元素(S)表示第k个保护的期望的状态;如果第k个保护应该动作(S)=1,否则(S)=0;R*(S)由S的状态决定;cj为一个nc维向量,表示nc个断路器的实际状态;C中第j个元素cj表示第j个断路器的实际状态,cj=0或1分别表示第j个断路器的未跳闸或跳闸状态;(S,R)为一个nc维向量,表示nc个断路器的期望的状态;(S,R)中的第j个元(S,R)表示第j个断路器的期望的状态;如果第j个断路器应该跳闸(S,R) =1,否则(S,R) =0;(S,R)由S和R的状态决定。
保护期望状态可按以下原则确定:
主保护期望状态 =元件状态
第1后备保护期望状态 =元件状态×(1-主保护状态)
第2后备保护和其它保护的情况要复杂一些,具体可参见文献[3]。

用图1所示的简单例子来说明如何确定C*和r*。图1中,保护1(r1)和2(r2)分别为元件s1的主保护和后备保护,都用于保护s1。
当s1故障时,r1应动作:

当s1故障且r1未动作时,r2应动作:

r1和r2只要有一个动作时,断路器c1应跳闸:
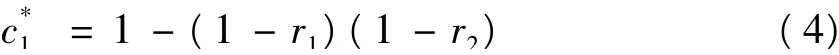
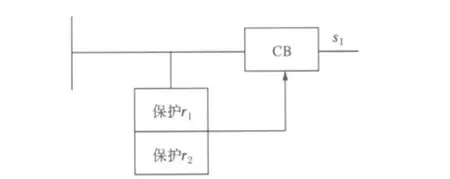
图1 故障诊断的简单例子Fig.1 Simple example of fault section estimation
故障元件的识别问题就是寻找能使取得最小值的S。显然这是一个0-1整数规划问题。
2 故障区域的快速识别
电力系统的元件发生故障后,有关的保护和断路器会动作切除故障,形成故障区域(或停电区域)。故障元件肯定在这些停电区域之中,因此故障诊断只需要对停电区域进行分析,从而可大大提高诊断速度。要确定停电区域,可以根据电力网络的拓扑关系形成连通图,连通图如果无源则为停电区域。具体方法参看文献[6]。
3 基于粒子群优化算法的电力系统故障诊断
3.1 量子粒子群优化算法
量子粒子群算法(QPSO)是一种新的能保证全局收敛的粒子群算法,由于在量子空间中,粒子位置和速度不能同时确定,遵循PSO算法的思想,粒子的状态在量子空间中不再用位置矢量和速度矢量表示,而是用波函数[9]来描述。由测不准原理,粒子的位置和速度不能同时精确测定,可以不考虑速度,而在空间表象中考查粒子。粒子出现在位置x的概率就由概率密度函数表示,而不限于既定的轨道函数。因此通过波函数(波函数的平方是粒子在空间中某一点出现的概率密度)来描述粒子的状态,并通过求解薛定谔方程得到粒子在空间某一点出现的概率密度函数,随后通过蒙特卡罗随机模拟的方式得到量子空间中粒子的位置方程。QPSO初始化为一群随机粒子,通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值”来更新自己。第一个极值就是粒子本身所找到的最优解,这个极值称为个体极值pbest。另一个极值是整个种群目前找到的最优解,这个极值是全局极值gbest。在QPSO算法中,粒子群按照下面的几个公式来更新自己在解空间的位置
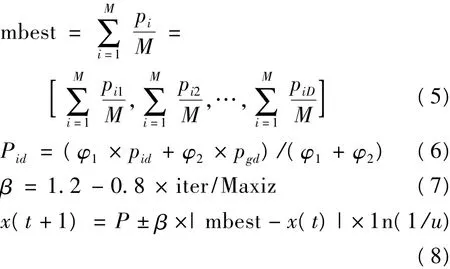
其中:式(5)中,M是种群数目,D是粒子的最大维数,d是粒子的维数,pi是第i个粒子的最好位置,pgd为种群中所有粒子经历的最好位置;mbest是所有粒子个体最佳位置的平均值;式(7)中,β为创造系数,iter为当前迭代次数,Maxiz为最大迭代次数;式(8) 中 x(t+1) 是粒子的当前位置;φ1、φ2,u都为0至1之间的随机数,当u≥0.5时,式(8)取“-”号,0 < u <0.5时取“+”号。
3.2 算法实现步骤
1) 初始化粒子、粒子个数、pbest、gbest、迭代次数、粒子的维数;
2)若未达到最大迭代次数,则根据式(1)计算每个粒子的E(S)适应值,更新pbest和gbest;若达到最大迭代次数,则跳转到步骤8;
3)为防止算法陷入局部最优,若某个粒子的位置等于种群最佳位置,将对该粒子的位置重新初始化赋值;
4)根据式(5)、(6)、(7)计算mbest、β和P值;
5)用式(8)更新粒子群的位置;
6)由于粒子的位置只有0、1两种状态,因此对函数值以0.5为分界点进行离散化,x(t)<0.5取值为0,否则取为1);
7)迭代次数加1,返回步骤2);
8)输出结果。
4 算例分析
为了验证粒子群优化算法在电力系统故障诊断中的优化效果,本文在图1所示的测试系统中对复杂故障进行测试。该测试系统共有28个元件、40个断路器和84个保护。
28个元件依次编号为 S1~S28:A1,…A4;T1,…,T8;B1,…,B8;L1,…,L8。
40个断路器依次编号为C1~C40:CB1,CB2,…,CB40。
84个保护中,36个为主保护,48个为后备保护。36个主保护依次编号为r1~r36:A1m,…,A4m;T1m,…T8m;B1m,…,B8m;L1Sm,…,L8Sm;L1Rm,…,L8Rm。48个后备保护依次编号为r37~r84:T1p,…,T8p;T1s,…,T8s;L1Sp,L1Rp,…,L8Sp,L8Rp;L1Ss,L1Rs,…,L8Ss,L8Rs。
在上述名称中,A和B表示母线,T表示变压器,L表示线路,S和R分别表示线路的送端和受端,m、p、s分别表示主保护、第一后备保护和第二后备保护。
对应于该测试系统发生复杂故障,警报信号为:保护 T7m、T8p、B7m、B8m、L5Sm、L5Rp、L6Ss、L7Sp、L7Rm、L8Ss动作,断路器 CB19、CB20、CB29、CB30、CB32、CB33、CB34、CB35、CB36、CB37、CB39跳闸。
具体诊断过程如下:
首先根据跳闸断路器形成的无源网络得出故障区域,如图2所示,从图2中得知需要进行故障诊断的元件为 L5、L6、L7、L8、B7、B8、T7、T8,对应的元件状态向量为S=[S1,…,S8];然后将已知的保护实际状态向量R、断路器实际状态C以及保护期望状态向量和断路器期望状态代入目标函数,利用量子粒子群优化算法求解上述0-1整数规划问题。其中,粒子的维数为8,种群数为20,最大迭代次数是30代。为了保证收敛到最优解,迭代收敛次数可以设置得比较大。
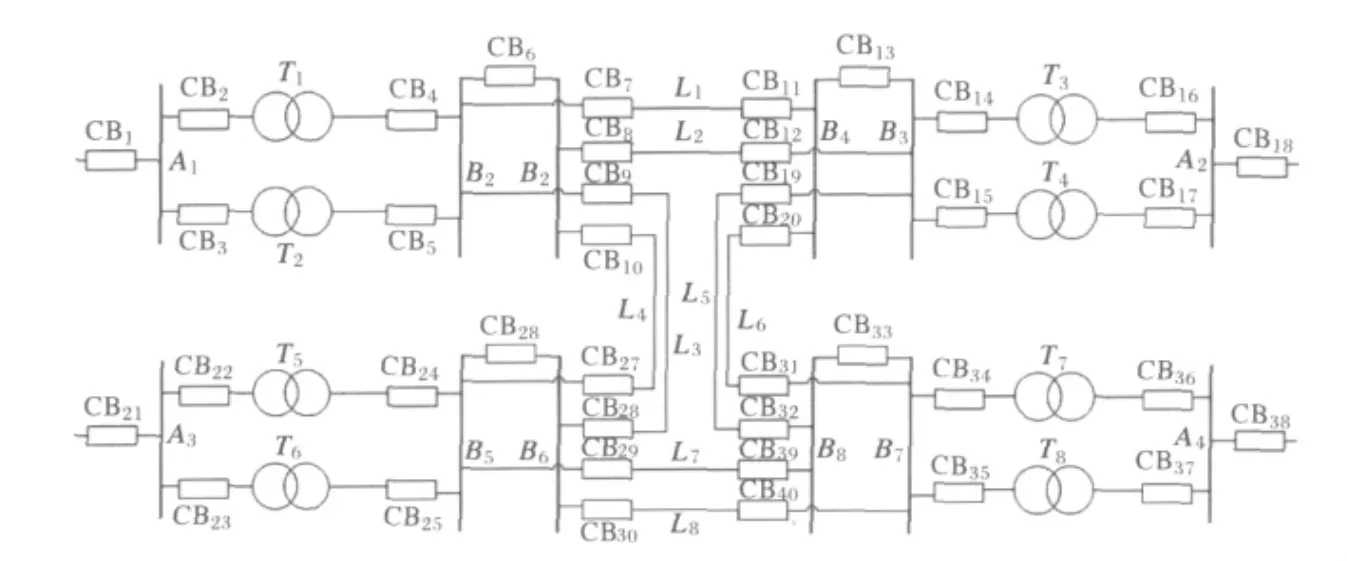
图2 测试系统图Fig.2 Diagram of the test system
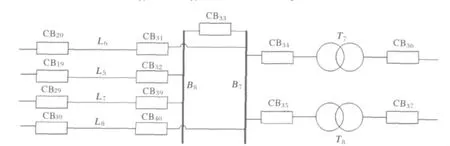
图3 故障区域图Fig.3 Fault districts
目标函数的表达式为:
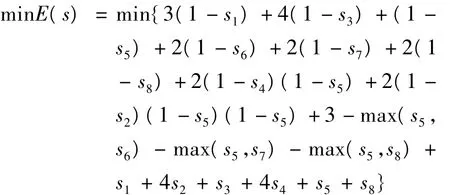
用Matlab仿真,结果如图4所示。
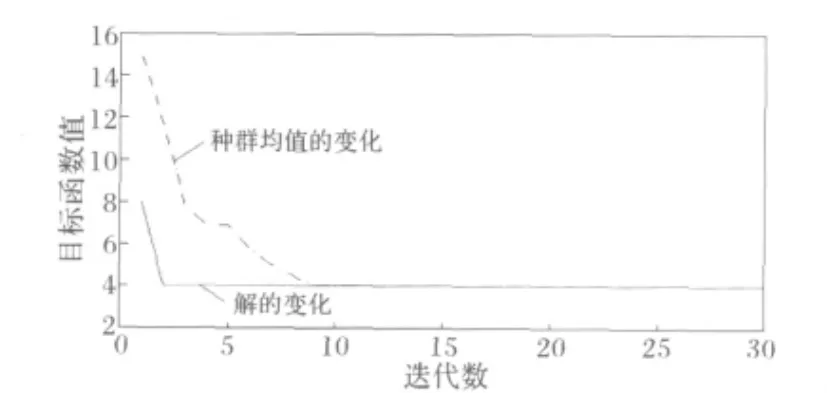
图4 QPSO的最优解和种群均值Fig.4 Optimal solution and the population mean of QPSO
从上图中可见,到第2代,粒子群优化算法已经搜索到最优解。种群均值的变化在10代以后趋于稳定。gbest=1 0 1 0 1 1 1 1,即问题的最优解为:S= [S1,S2,S3,S4,S5,S6,S7,S8]= [1,0,1,0,1,1,1,1],诊断结果为线路 L5、L7,母线 B7、B8和变压器T7、T8故障。E(S)最小值 =4。
根据保护和断路器的报警信号,以及诊断结果,可以分析得知,线路 L5、L7,母线 B7、B8和变压器T7、T8发生故障时,线路L5的S侧主保护L5Sm,线路L7的R7侧主保护L7Rm动作,母线B7、B8的主保护B7m、B8m正确动作,变压器T7主保护T7m动作。由于线路L5的R侧主保护L5Rm未能正确动作,L5的R侧第一后备保护L5Rp动作,同理,L7的S侧第一后备保护L7Sp动作,变压器T8第一后备保护T8p动作,这些保护动作之后,断路器 CB19、CB29、CB31、CB32、CB33、CB34、CB35、CB36、CB37、CB39和 CB40应该跳闸,但是断路器 CB31、CB40拒动,线路 L6、L8的 S侧第二后备保护L6Ss、L8Ss动作,将断路器CB20、CB30切断,避免故障的进一步扩大。这是一个存在主保护和断路器拒动的多重复杂故障,使用上面的方法仍可以准确而快速地诊断故障元件。
从图4中可以看出10代以后,种群中的每个粒子搜索到了最优解,种群取值趋于稳定。
20个种群每个粒子的目标函数表达式是相同的,刚开始搜索时目标函数值是不同的,随着搜索过程的进行,每个粒子都会朝着最优的方向飞行,就像鸟群寻找食物一样,最终都会找到食物。见图5所示。

图5 QPSO每代种群中每个粒子的目标函数值Fig.5 Particle's fitness value of all generationsQPSO
用标准的PSO算法和传统的遗传算法求解上述0-1整数规划问题,由于它们只能求解最大化问题,因此为便于求解,须将使式(1)最小化的问题改为使式(9)最大化问题:
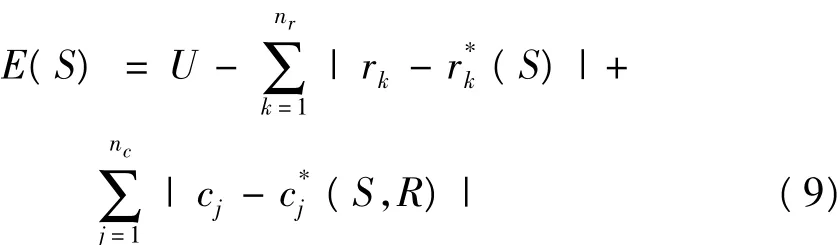
式中,U为任意给定的很大的正数,用于确保E(S)恒为正,本文中取U=50。用标准PSO求解时,粒子的维数为8,种群数为20,C1=0.7,C2=0.7,最大迭代次数是30代。结果如图6所示。

图6 标准PSO的最优解变化和种群均值变化Fig.6 Optimal solution and thepopulation mean of normal PSO
从图6、7中可以看到标准PSO算法比量子粒子群算法收敛速度慢,但比传统的遗传算法快。稳定性能比遗传算法的好。
用遗传算法求解,其中种群数40,迭代次数为50,结果如图8和9所示。
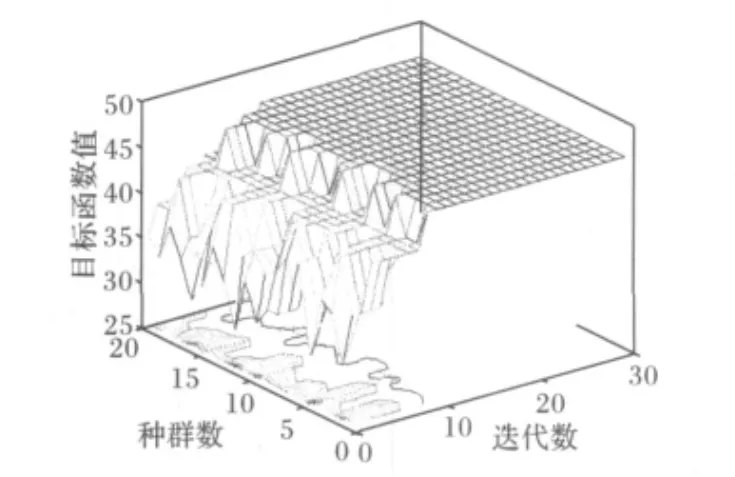
图7 标准PSO每代种群中每个个体的目标函数值Fig.7 Particle's fitness value of all generations of PSO

图8 GA的最优解变化和种群均值变化Fig.8 Optimal solution and the population mean of GA
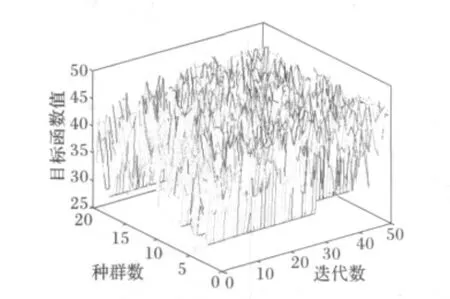
图9 GA每代种群中每个个体的目标函数值Fig.9 Particle's fitness value of all generations of GA
从图5中可以看到利用传统的遗传算法求解,搜索到第7代才搜索到最优解,而且不稳定。种群均值的变化也比较大。由图6中也可以清楚地看到这一点。每代种群每个个体的目标函数值取值比较分散。三种算法分别运行20次,所得出的结论与上述一样。
通过三种算法仿真比较,表明采用量子粒子群优化算法只须较少的种群数和迭代次数就可以得到质量较高的最优解,说明该算法具有良好的收敛稳定性。
另外,用量子粒子群优化算法测试了多种故障情况,结果都找到了全局最优解,且收敛快稳定性好。这里由于篇幅所限就不再论述了。
5 结语
本文在电力系统故障诊断中引入量子粒子群优化算法,并将诊断方法与标准PSO算法和传统的遗传算法方法进行比较,通过仿真表明量子粒子群优化算法不仅能够正确诊断,而且具有很好的收敛速度和稳定性。因此作为一种新的应用,该方法具有理论和实际的意义。
[1]毕天姝,焦连伟,严正,等(Bi Tianshu,Jiao Lianwei,Yan Zheng,et al).用于分布式故障诊断系统的新型网络分割法(Graph partitioning method for distributed fault section estimation system in power networks)[J].电力系统自动化(Automation of Electric Power Systems),2001,25(16):16 -21.
[2]文福拴,钱源平,韩祯祥,等(Wen Fushuan,Qian Yuanping,Han Zhenxiang ,et al).利用保护和断路器信息的电力系统故障诊断与不可观测的保护的状态识别的模型与Tabu搜索方法(A Tabu search approach to fault section estimation and state identification of unobserved protective relays in power systems using information from protective relays and circuit breakers)[J].电工技术学报(Transaction of China Electrotechnical Society),1998,13(5):1 -8,51.
[3]文福拴,韩祯祥,田磊,等(Wen Fushuan,Han Zhenxiang,Tian Lei,et al).基于遗传算法的电力系统故障诊断的解析模型与方法——第一部分:模型与方法(An analytic and genetic algorithm based methods for fault diagnosis in power systems Part 1:The model and method)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),1998,10(3):1 -7.
[4]文福拴,韩祯祥,田磊,等 (Wen Fushuan,Han Zhenxiang,Tian Lei,et al).基于遗传算法的电力系统故障诊断的解析模型与方法——第二部分:软件实现(An analytic and genetic algorithm based methodsfor fault diagnosis in power systems Part 2:The software implementation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),1998,10(3):8 -14,22.
[5]文福拴,韩祯祥,田磊,等(Wen Fushuan,Han Zhenxiang,Tian Lei,et al).基于遗传算法的电力系统故障诊断的解析模型与方法——第三部分:浙江电力系统EMS信息获取与测试结果(An analytic and genetic algorithm based methods for fault diagnosis in power systems Part 3:The EMS data acquisition method and test results for Zhejiang province power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),1999,11(1):13 -18,52.
[6]孙伟,李林川,卢庆聪,等(Sun Wei,Li Linchuan,Lu Qingchong,et al).基于停电区域的电力系统故障诊断的一种新模型(A new method for power system fault diagnosis based on power supply interrupted region)[J].电网技术(Power System Technology),2004,28(5):30-34.
[7]Eberhart R C,Shi Y.Particle swarm optimization:developments,applications and resources[C]∥ IEEE Conference on Evolutionary Computation,Soul,Korea:2001.
[8]El-Gallad A,El-Hawary M ,Sallam A ,et al.Enhancing the particle swarm optimizer via proper parameters selection[C]∥Canadian Conference on Electrical and Computer Engineering,Winipeg,Canada:2002.
[9]Sun Jun,Feng Bin,Xu Wenbo.Particle swarm optimization with particles having quantum behavior[C]∥IEEE Congress on Evolutionary Computation ,Portland,USA:2004.
