随机子空间法在低频振荡分析中的应用＊

袁荣湘，江保锋，赵树华，陈剑锋，方永康，吴路力，黄凯荣

(1.武汉大学电气工程学院，武汉 430072;2.广东电网公司江门供电局，江门 529000)

低频振荡现象是电力系统稳定运行中备受关注的重要问题之一，其在线监测与离线分析也是广域测量系统 WAMS(wideareameasurement system) 应用的重要组成部分［1～3］。特征值分析法［4，5］是进行电力系统低频振荡研究的一种经典方法，但其计算量大，计算速度慢，不能满足在线分析的要求［6］。目前应用较广的是Prony及其改进方法［6～9］，但 Prony 算法对噪声比较敏感，模型阶数的确定也较为困难，往往需要增加阶数来提高辨识精度，增加了算法的复杂度和计算代价。基于总体最小二乘法TLS(total least squares)和旋转不变技术估计信号参数ESPRIT(estimation of signal parameters via rotational invariance techniques)的方法(简称TLS-ESPRIT算法)也已应用于低频振荡分析［10］，该方法突出的优点是抗噪能力强，辨识精度高，由于需要进行两次奇异值分解，使得计算时间稍长。

本文将随机子空间辨识方法［11］SSI(stochastic subspace identification)应用于电力系统低频振荡模式辨识，随机子空间法是近年来发展的一种线性系统辨识方法，可以有效地从环境激励的结构响应中获取模态参数。其核心是把“将来”的输出行空间投影到“过去”的输出行空间，投影结果是保留了“过去”的全部信息，并用此预测“未来”。采用简单可靠的数学工具如矩阵的正交三角分解QR(QR factorization)和奇异值分解SVD(singular value decomposition)获取状态矩阵及其特征值，结合最小二乘法，得到信号的振荡参数。

1 随机子空间辨识方法

1.1 状态空间方程

随机子空间识别方法是以线性的离散状态空间方程为基础的:

式中:xk=x(kΔt)是n维离散状态向量，Δt为采样周期;yk是l维输出向量;A∈Rn×n为离散的系统矩阵;B∈Rn×m为输入矩阵;uk∈Rm为输入向量;C∈Rl×n是输出矩阵;D∈Rl×m表示直接传递系数矩阵。

实际测量中总是存在着系统的不确定性，即随机分量(噪声)，考虑过程噪声wk和测量噪声vk时，式(1) 可以写成［12］:

产生低频振荡时，由于输入(激励)uk一般难以测得，只能得到系统的响应信号序列(功角、有功等)，可建立系统的随机状态空间模型:

满足:

其中，wk∈Rn、vk∈Rl是不可测、高斯零均值白噪声序列，E是数学期望，δkl是Kronecker函数。Q∈Rn×n、S ∈ Rn×l和 R ∈ Rl×l是噪声序列 wk和 vk的协方差矩阵。

1.2 随机子空间辨识基本方法

随机子空间识别有3种不同的方法［13］，应用于低频振荡分析时，根据采样信号(即输出)求出状态矩阵A，可按如下步骤进行［14］。

1)由输出的N点采样数据构造Hankel矩阵如下，下标p表示“过去”的采样数据，f表示“未来”的采样数据。i＞＞n，当全部采样点数据都用到时，N=2i+j－ 1。

2)计算Yp和Yf的协方差矩阵Rfp并作SVD的分解:

U1∈ Rli×n，U2∈ Rli×(li－n)、S1、S2包含了 Rfp的奇异值，通过奇异值的分布可求得系统阶次n［15］，即前n个奇异值占主导。

3)系统的广义可观测矩阵Γi可取为

由下式可求出状态矩阵A:

式中Γi(1∶l，∶)表示取Γi的第1到l行所组成的矩阵。

4)得到系统的状态矩阵A后，求其特征值λi(i=1，2，…，n)，设采样时间间隔为 Δt，则信号的频率fi和阻尼比ξi为:

5)通过最小二乘法求得各分量的幅值和相角。由N点采样信号，有:

式中:

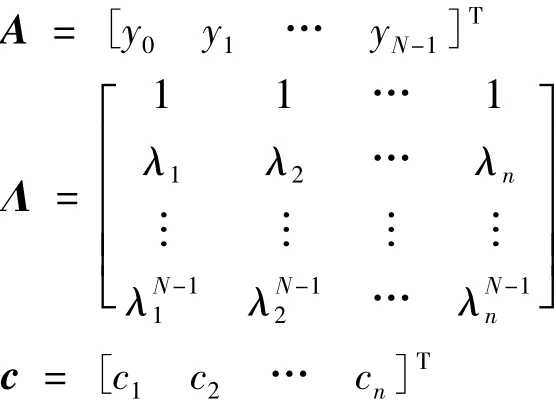
则c的最小二乘解为

各分量的幅值Ai和相位φi为

至此，低频振荡的各参数都已求得。整个计算过程可分两大步骤，即随机子空间辨识得到系统矩阵、求振荡模式的各参数，简单可靠，便于应用。

2 仿真算例

2.1 合成信号分析

按下式产生一理想信号:

此信号包含两个振荡模式。在此理想信号上叠加幅值为10的白噪声作为测试信号来验证算法的有效性。数据采样时间为(0～10)s，采样频率为50 Hz(采样间隔0.02 s)。

由于低频振荡的频率集中在0.1～2 Hz，过密的采样会带入不必要的高频信号，所以输入信号的采样率不必过高，一般可选用不高于20 Hz采样率的数据。因此将原数据降低3倍采样率后(采样间隔为0.06 s)再用于辨识，不仅能降低高频噪声的影响，而且计算速度也大大加快。随机子空间法辨识结果与理论值的比较见表1，图1给出了辨识结果拟合原数据的效果图。

表1 随机子空间法辨识结果与理论值比较Tab.1 SSI method compared with the theoretical value

通过比较发现，此方法能较准确地辨识出信号各模式的频率、阻尼比、幅值和相角，具有很高的频率分辨率。由于子空间辨识方法本身的特点，使得其抗噪能力较强。算法主要计算量为一次SVD分解和一次特征值分解，快速有效。

图1 辨识结果拟合原数据效果图Fig.1 Effect picture of identification results fit original data

2.2 仿真数据分析

四机两区系统接线图见图2，具体参数见文献［16］。在正常运行方式下，增加母线7上的负荷，记录联络线上传送的有功功率，采样频率为60 Hz，共541个采样点，其波形见图3，可直观地看出联络线上的功率发生了增幅振荡。

图2 四机两区系统接线图Fig.2 Wiring diagram of four machine two area system

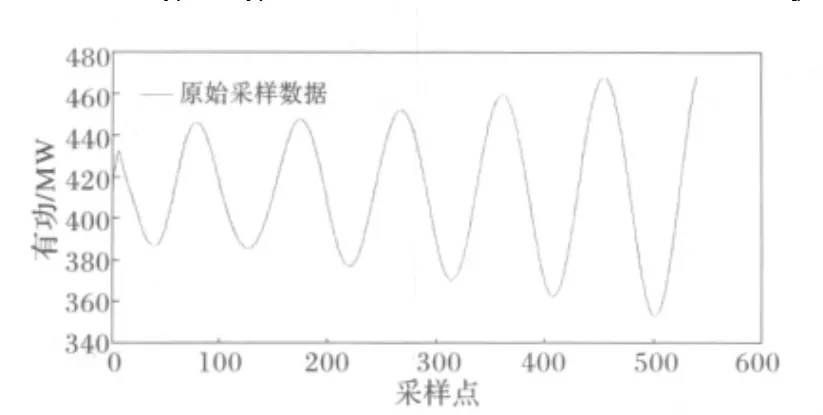
图3 联络线上的有功波形Fig.3 Positive power waveform of the tie line

对采样数据进行均值法去直流和重采样(见2.1)后，用随机子空间法辨识振荡的主导模式。为了便于比较，同时给出扩展Prony方法［15］的辨识结果，见表2。原数据和随机子空间法辨识结果拟合波形见图4。

从表2可以看出，联络线上的有功发生了频率为0.64 Hz的低频振荡，为区间振荡模式。Prony辨识结果也印证了随机子空间法的正确性，同时，随机子空间法的计算时间约为Prony方法的一半(Windows XP系统，C语言)，可以满足在线应用的要求。

表2 随机子空间法和Prony法辨识结果比较Tab.2 SSI method compared with Prony algorithm

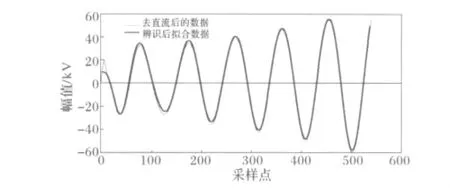
图4 去直流后的数据和随机子空间辨识结果拟合波形Fig.4 Waveform of SSI method results fit data of cutting DC

3 结语

随机子空间法辨识精度高，抗噪声干扰能力强，算法时间复杂度低，快速有效，辅以必要的数据预处理，如FIR低通滤波［17］和降低采样频率(实际系统可选用不高于20 Hz采样率的数据)，可更好地满足在线辨识要求。由于随机子空间辨识是基于多输出的辨识方法，所以既可用于单信号辨识，如在线监测发电机功角和联络线功率，也可以用多路采样信号同时辨识出地区模式和系统间模式，如离线研究，充分满足广域测量系统(WAMS)的应用需求。

［1］常乃超，兰洲，甘德强，等(Chang Naichao，Lan Zhou，Gan Deqiang，et al).广域测量系统在电力系统分析及控制中的应用综述(A survey on applications of wide-area measurement system in power system analysis and control)［J］.电网技术(Power System Technology)，2005，29(10):46 －52.

［2］邱夕兆，于占勋，雷鸣，等(Qiu Xizhao，Yu Zhanxun，Lei Ming，et al).山东电网基于WAMS的低频振荡统计与评估(WAMS based statistics and assessment of low frequency oscillation in Shandong power grid)［J］.电力系统自动化(Automation of Electric Power Systems)，2008，32(6):95 －98.

［3］董明齐，杨东俊，黄涌(Dong Mingqi，Yang Dongjun，Huang Yong).2008年冰灾期间华中电网WAMS系统实测低频振荡事件分析(Analysis on the low frequency oscillation incidents measured by WAMS of central China power grid during the 2008 ice hazard)［J］.华中电力(Central China Electric Power)，2008，21(5):22－25.

［4］孙建生，侯志俭，王承民(Sun Jiansheng，Hou Zhijian，Wang Chengmin).Arnodli算法在电力系统静态电压稳定分析中的应用(Application of Arnodli algorithm to the steady-state voltage stability analysis of power systems)［J］.电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2005，17(5):79 －81，98.

［5］宗秀红，张尧，武志刚(Zong Xiuhong，Zhang Yao，Wu Zhigang).交直流混合系统低频振荡的概率特征根分析(Probabilistic eigenvalue analysis for low frequency oscillation of AC/DC parallel systems)［J］.电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2006，18(6):13 －17.

［6］肖晋宇，谢小荣，胡志祥，等(Xiao Jinyu，Xie Xiaorong，Hu Zhixiang，et al).电力系统低频振荡在线辨识的改进Prony算法(Improved Prony method for online identification of low-frequency oscillations in power systems)［J］.清华大学学报(自然科学版)(Journal of Tsinghua University(Science＆Technology))，2004，44(7):883 －887.

［7］Trudnowski D J，Johnson J M，Hauer J F.Making Prony analysis more accurate using multiple signals［J］.IEEE Trans on Power Systems，1999，14(1):226 －231.

［8］马燕峰，赵书强，刘森，等(Ma Yanfeng，Zhao Shuqiang，Liu Sen，et al).基于改进多信号 Prony算法的低频振荡在线辨识(Online identification of low-frequency oscillations based on improved multi-signal Prony algorithm)［J］.电网技术(Power System Technology)，2007，31(15):44 －49，90.

［9］鞠平，谢欢，孟远景，等(Ju Ping，Xie Huan，Meng Yuanjing，et al).基于广域测量信息在线辨识低频振荡(Online identification of low-frequency oscillations based on wide-area measurements)［J］.中国电机工程学报(Proceedings of the CSEE)，2005，25(22):56 －60.

［10］张静，徐政，牛卢璐，等(Zhang Jing，Xu Zheng，Niu Lulu，et al).TLS-ESPRIT在电力系统信号高精度频谱估计中应用(Application of TLS-ESPRIT in high resolution spectrum estimation of power system signal)［J］.电力自动化设备(Electric Power Automation E-quipment)，2009，29(5):48 －51.

［11］Van Overschee Peter，De Moor Bart.Subspace algorithms for the stochastic identification problem［C］∥The IEEE Conference on Decision and Control，Brighton，England:1991.

［12］Peeters Bart，De Roeck Guido.Reference － based stochastic subspace identification for output only modal analysis［J］.Mechanical Systems and Signal Proceeding，1999，13(6):855 －878.

［13］Peter Van Overschee，Bart De Moor.Subspace Identification for Linear Systems:Theroy-Implementation－Applications［M］.Dordrecht，Netherlands:Kluwer Academic Publishers，1996.

［14］Katayama T.Subspace Methods for System Identification［M］.London:Springer，2005.

［15］张贤达.现代信号处理［M］.北京:清华大学出版社，2002.

［16］Prabha Kunder.Power System Stability and Control［M］.USA:McGraw － Hill Companies，1994.

［17］郑君里，应启珩，杨为理.信号与系统(第二版，下册)［M］.北京:高等教育出版社，2000.