基于小波变换的代谢网络比较方法*
2011-08-14彭佳扬杨路明
彭佳扬,罗 永,杨路明,李 敏,赵 岩,成 磊
(1.中南大学 信息科学与工程学院,湖南 长沙 410083;2.国防科学技术大学 理学院,湖南 长沙 410073)
随着多物种的全基因组测序的完成以及基因组注释信息的日益完善,使得可以从基因组信息较为可靠地重构物种特异的代谢网络[1-2].代谢网络的重构使得研究者可以从整体水平上来分析物种间的进化关系.然而物种整体水平上的代谢网络是由很多代谢通路交联而成,过于庞大和复杂,从而对整个网络进行逐个元素的比对,复杂度特别高.越来越多的研究者开始关注用网络比对方法来确定网络间的进化距离.
现阶段确定代谢网络间进化距离的策略主要有两种:分别是基于通路比对的通路水平上的网络比对和物种水平上的全网络比对.基于通路比对[3-5]的方法是从每个待研究物种的代谢网络中选取一条共有的、且相对保守的代谢通路(如三羧酸循环或糖酵解通路),然后通过对每对代谢网络中的该条代谢通路元素进行逐个比对,来确定通路间的差异,即代表物种间的进化距离.基于全网络比较的方法通常将物种的整个网络简单地看成一个节点集合,然后通过集合论方法,通过计算集合间距离的函数,如Jaccard距离或Hamming距离等,来确定网络间的进化距离.2004年,Agruilar等人[6]将物种的酶图表示成酶的集合,并根据物种中酶的出现或缺失进一步将物种特异的酶集合表示成0-1向量,然后通过计算归一化后的Hamming距离得到向量间距离,最终构建出物种间的进化距离矩阵;2004年,Ma等人[7]将重构的82个物种特异的代谢网络表示为物种特异的酶集合,然后计算Jaccard系数、Simposon系数和Korbel系数来衡量集合间的距离,以此来确定代谢网络间的进化距离;2006年,Forst等人[8]将代谢网络表示为“干净的”代谢物-反应二部图,通过计算平凡Jaccard距离这一度量函数来获得网络间的进化距离;2006年,Tohsato等人[9]则将物种特异的代谢网络表示为酶促反应集合,根据平凡Jaccard距离来计算物种特异的酶促反应集合之间的差异,从而得到代谢网络的进化距离矩阵.2008年,周婷婷等人[10]加入了酶的特征来计算进化距离,提出了一种确定进化距离的WJD模型,并分析和评价了其合理性.
目前的这些计算代谢网络间进化距离的方法大都是基于集合论的方法.该方法仅仅是将网络抽象成节点的集合,并根据节点集合的差异来确定不同网络间的距离,而没有考虑到节点本身的特性以及网络拓扑结构属性方面的差异,因此这类网络比较方法还有待改进.本文建立了代谢网络的相关数学模型,主要运用小波时频分析方法,结合主成分分析法对代谢网络进行相似性分析.首先用主成分分析法提取代谢网络节点的7个中心性拓扑属性参数的主成分,因为主成分是无序的,接下来通过统计的手段对降维的主成分数据进行有序化,最后为了提取有序化后的主成分曲线趋势,利用小波时频分析方法提取低频信号作为代谢网络的特征曲线,用以比较不同代谢网络的相似度,由此推算出代谢网络的进化距离.
1 网络节点的中心性拓扑参数
在研究复杂网络时,通常用节点的中心性度量来衡量节点在网络中影响能力的大小,通过网络的拓扑属性可了解该对象获得、控制信息及资源的能力.在无向网络中,度中心性测度(简称节点度或度)是最常用的测度,此外常用的节点测度还包括聚集系数、中介数、接近度、信息度、子图和特征向量等,在具体分析中我们也称这些测度为参数.
定义1 节点的度中心性(Degree Centrality,DC)[11]:某个节点的度定义为与节点i相连的节点个数,记为d(u).在代谢网络中表示与这个酶作用的酶的数量.从直观上看,节点度越大意味着该节点在某种意义上越重要,在节点关系上具有某种优势.
定义2 聚集系数中心性(Clustering Coefficient,CU)[12]:某个节点的聚集系数刻画了这个节点周围的节点彼此之间联系的紧密程度,整个网络的聚集系数CU就是所有节点聚集系数CUu的平均值.度为d(u)的节点u,其d(u)个邻居之间实际存在的边数Eu与它们之间最多可能边数d(u)(d(u)-1)/2之比即为u的聚集系数,即:

定义3 中介系数中心性(Betweenness Centrality,BC)[13]刻画节点在节点对之间通信的影响程度,被定义为网络所有的最短路径中经过当前节点的数目.它反映节点在特定网络拓扑结构中所处位置的枢纽程度,通过它可以有效地区别出模块内、外的边.如果ρ(i,j)表示从节点i到节点j最短路的条数,而ρ(i,j,k)是在这些最短路径中经过节点k的数量,因此,k节点的中介数为:
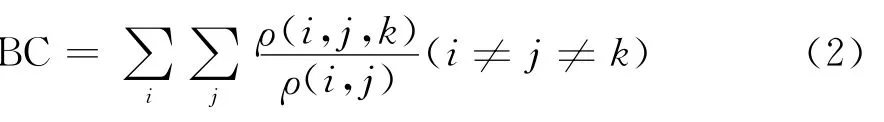
定义4 接近度中心性(Closeness Centrality,CC)[14]:如果节点与网络中所有其它节点的距离都很短(距离之和最小),那么它的接近度就高,因此该测度在一定程度上能够反映出节点在全局或整体上的中心程度.设μuv是节点u与节点v之间的距离,那么节点u的接近度为:

定义5 信息中心性(Information Centrality,IC)[15]:Newman认为信息中心性实际上是另一种接近度,本质上是测量以节点u为端点的路径的调和平均长度,如果u通过许多短的路径与其他节点相连则意味着其平均路径长度小而信息度(接近度)大.如果A是一个网络的邻接矩阵,D是各节点的度的对角矩阵,J矩阵是所有的元素均为1的矩阵.那么IC可定义为通过倒转矩阵B,而B=D-A+J,从而得到矩阵C=(cij)=B-1,信息矩阵Iij=(cii+cjj-cij)-1,那么第i个节点的信息中心值可通过下式的调和平均值来定义:

定义6 子图中心性(Subgraph Centrality,SC)[16]:表示网络节点出现在不同连通子网中的次数,即:

其中μl(i)是以节点i开始和结束的步长数,即:从i节点开始的经过L步再回到起点的闭路数.(v1,v2,…,vn)是RN的一个正交基 ,RN是由A矩 阵的特征向量组成的矩阵,这些特征向量分别与相关的特征值λ1,λ2,…,λn对应.vj(i)是Vj的第i个元素.
定义7 特征向量中心性(Eigenvector Centrality,EC)[17]定义为网络的邻接矩阵A的主特征向量.它模拟了一种各个节点同时影响其邻居节点的程度的机制.这种特征向量的决定公式为λe=Ae,其中A是图的邻接矩阵,λ是特征值,e是特征向量.因此,节点i的EC定义为特征向量e1的第i个元素e1(i),而e1对应于A矩阵的最大的特征值λ1,如下列公式(6)所示:

如果一个节点具有较高的特征向量评分,那么这个节点被认为是关键的,这意味着与其毗邻的其他节点也具有较高的得分数.
2 主成分分析
将包含各方面拓扑信息的7个节点中心性进行主成分分析,得到一个网络中心性参数.
2.1 选取主成分
主成分分析方法(PCA)[18]是将原来较多的指标简化为少数几个新的综合指标的多元统计方法.PCA能够用较少的几个综合指标尽量多地反映原来较多变量指标所反映的信息,同时它们之间又是彼此独立正交的.这些互相正交的新变量是原先变量的线性组合,叫做主成分.
记X1,X2,…,Xn为原变量指标,F1,F2,…,Fp为新变量指标,n≥p.主成分分析实际上是做一个线性变换:

满足如下条件:
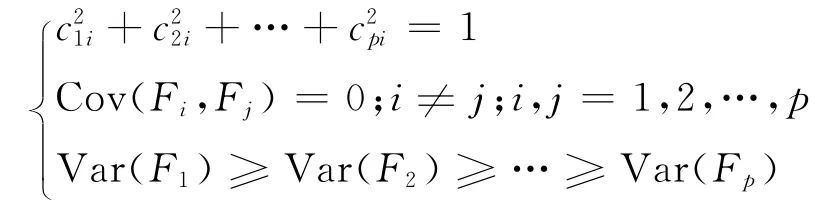
每个主成分的系数平方和为1;且主成分之间相互独立,即无重叠的信息;Var(F1)为方差函数,每个成分的方差依次递减,重要性依次递减.
对代谢网络中n个节点的p个中心性进行主成分分析 PCL(si)= PCL(si1,si2,…,sip),i= 1,2,…,n,选取其主成分si0,具体的实现步骤如图1所示.
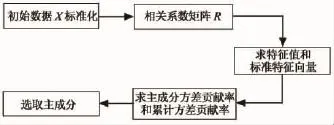
图1 选取主成分实现步骤Fig.1 The process of select principal component
设原始数据矩阵为X,n为代谢网络中节点的个数,p为中心性属性的个数,且

1)对矩阵X中的原始数据进行标准化处理.
将原始数据矩阵X进行标准化,得到标准化后的协方差矩阵;计算平均值和标准方差的公式为:

2)建立标准化后的p个指标相关系数矩阵R= (rij);i,j=1,2,…,p,其中rij的计算公式为:

3)求相关系数矩阵R的特征值和特征向量,并对特征值和特征向量按照特征值的大小进行排序.排序后特征值为λ1≥λ2≥…≥λn≥0.相应的标准化,正交特征向量为:
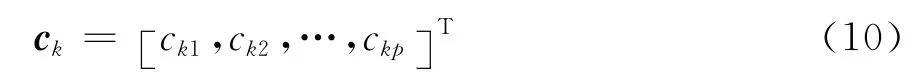
4)计算各主成分的方差贡献率Qt和累积方差贡献率qt.确定主成分个数,再求出各样本的主成分值矩阵,并以每个主成分的方差贡献率为权数计算各样本的综合评价值.其中,方差贡献率qt表示第t个主成分提取原始n指标的信息量,累计方差贡献率Qt表示前t个主成分保留的原始信息量.计算公式如下:

5)确定主成分个数有两种方法:一种是使前t个主成分的累积方差贡献率达到一定的要求,如可取Qt≥80%,这是实际中常用的一种方法.第二种是采用平均数原则,选用特征值大于1的所有指标.由于第一主成分在主成分中占有很大的比重,可以表示出大部分的特征信息.为易于计算比较,本章采用第一种方法,选取第一主成分为研究对象.
6)确定第一主成分中心性数值si0(i=1,2,…,n),以累积方差贡献率q(i)(i=1,2,…,p)为因子作上述种中心性的线性组合得到第一主成分中心性数值:
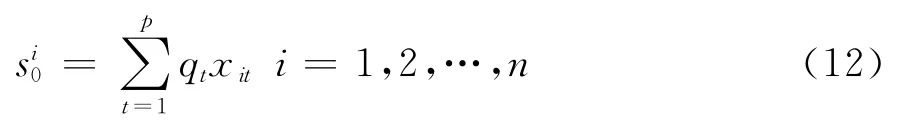
2.2 主成分数据序列化
主成分分析得到的数据是无序的,为了分析方便,需要将主成分数据序列化.首先搜索数据的最大值M和最小值m,设梯度等级为N(N的取值大小可由网络中节点数目多少而定,但必须是2的幂次,易于小波计算),将区间[m,M]N等分,每个区间的长度为h= (M-m)/N.然后判断每个主成分数列的元素的值,将每个区间包含的主成分元素的个数记为zi,Z= {zi=Count[(m+i)h≤si≤m+(i+1)h],i=0,1,2,…,N-1},其中Count为记数函数.
图2是对物种hsa的代谢网络处理得到的结果.先用主成分法提取代谢网络中所有节点中心性的第一主成分,并对其数值进行统计,将数值从最小值到最大值划分128等分,统计每一等分内节点的个数并归一化,即可得到此图,从而完成数据有序化.
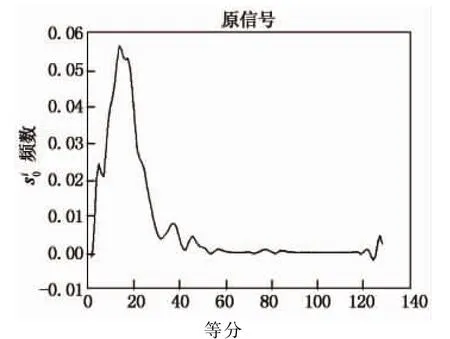
图2 物种hsa代谢网络的主成分数据有序化Fig.2 The principal components sequence of hsa
有序化后的主成分数据分布图可以作为一种特征曲线来反映代谢网络内在的某些特征.本文的主要工作就是将代谢网络的这种特征曲线提取出来,通过比较不同代谢网络的特征曲线之间的相似度,总结特点,发现规律.
3 小波分析与相似性比较
3.1 小波分析
小波分析[19]是运用傅里叶(Fourier)变换的局部化思想,进行时空序列分析的一种数学方法,是在L2(R)空间内利用小波基函数对数学表达式展开与逼近.它是一种函数的快速高效、高精度的近似方法.从信号处理的角度来看,作为一种新的时频分析工具,小波克服了Fourier分析方法无法反映时间域上局部信息的缺陷.对于代谢网络信息的局部性质描述和相似性比较具有重要的意义.
代谢网络拓扑属性的主成分序列化数据是一种典型的非平稳信号,利用小波实施时频分析时,由于同时具有时间和频率的局部特性以及多分辨分析特性,使得对非平稳信号的特征处理变得相对容易.
应用小波的Mallat算法对主成分序列化后的主成分信号进行小波分解.令信号T=Hif,则其为能量有限信号f∈L2(R)在分辨率2j下的近似,Hif可以通过低通滤波器分解为f在分辨率2j-1下的近似Hi-1f,通过高通滤波器Hif分解得到分辨率2j-1与2j之间的细节Di-1f,其分解过程如图3所示.
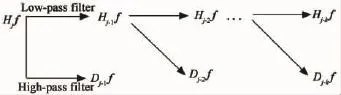
图3 主成分序列化信号小波频率分解示意图Fig.3 The wavelets decomposition for aprincipal components sequence
图4反映了小波强大的滤波功能,它可以将主成分序列化后的原始信号(如图2)分解为低频信号和高频信号两部分.低频信号主要反映了原始信号中的主要部分,如图4(a)所示,而高频部分则是对局部细节特征的提取,如图4(b)所示.本文主要利用小波变换提取低频信号,研究曲线的整体趋势.

图4 物种hsa代谢网络小波频率分解实例图Fig.4 The signal wavelets transformation of hsa
3.2 主成分特征相似性
因为主成分数据序列化后的曲线可以作为一种特征曲线来反映代谢网络拓扑上的内在特征,所以我们提取不同物种的小波低频信号,比较它们的相似程度,即可得到两物种的相似度,相似度定义如下.
定义8 设经过J次小波低通滤波的主成分序列化信号为W= (w0,w1,…,wN-1),为了比较两个信号W=(w0,w1,…,wN-1)和W*=(w*0,w*1,…,w*N-1)的近似程度,两小波信号的相似度定义为:

其中wk为对应在第k个区间内节点的个数.由定义式可知rW,W*∈ [-1,1],当rW,W*=1时信号W=W*,此时信号的相似程度达到最高.
4 基于主成分分析和小波变换的代谢网络比较方法MWD
由于主成分分析法能够降维并进行多参数分析,因此引入了主成分分析法来处理7个中性能参数,从而达到综合描述网络的中心性的目的.另一方面,小波分析能研究曲线的变化趋势,因此运用小波低频系数来研究序列化的主成分趋势特性,从而为研究生物进化提供理论和数学基础.
基于主成分分析和小波分析的生物代谢网络比较方法MWD,首先在计算得到7维(7种中心性参数)网络节点中心性基础上,用主成分分析法(PCA)对7维数据提取主成分处理得数据A0,并基于统计方法构造主成分有序化数列.然后运用小波得到特征信号W,最后由公式计算相似度rW,W*.通过rW,W*可以比较两个物种,推算出两物种代谢网络的距离,并推断出它们之间的进化关系.
方法MWD的具体步骤如下:
步骤1 由数据库中代谢网络的数据,利用7个中心性参数的定义,对网络中的第i个节点用7维数组si= (si1,si2,…,si7),i=1,2,…,n进行描述;
步骤2 运用主成分分析方法提取多个中心性参数 的 主 成 分,PCL(si)= PCL(si1,si2,…,si7)=(si0);
步骤3 对主成分分量{si0,i=1,2,…,n}序列化,取N=128进行序列化得到Z=(z1,z2,…,z128);
步骤4 对序列化数据Z= (z1,z2,…,z128)进行7次小波分解(这里的小波分解次数为7,只是一个经验参数,并不是不可改变的,它是经过多次实验比较实验效果而确定的,经过7次小波分解的信号所得出的低频信号平滑程度较好,较接近真实的信号)即令T=H7f,则经过7次小波低通滤波,序列化数据Z= (z1,z2,…,z128)变为特征信号(记为W数列)W= (w1,w2,… ,w128);
步骤5 对不同的网络分别得到特征信号W和W*,并由式(13)计算出不同网络的相似度rW,W*,对网络比较进行量化.
5 实 验
5.1 相似性比较结果及分析
实验数据来自于周婷婷等[2]基于KEGG LIGAND数据库重建的代谢网络.本章对此数据集中的109个不同进化阶段的代谢网络进行了分析.为了探讨物种的代谢网络是否具有结构特异性,将三个进化阶段物种的代谢网络分别与三组随机网络进行比较;为了证明代谢网络的进化是有一定规律的,将同一进化阶段不同物种代谢网络间进行比较、不同进化阶段的不同物种代谢网络间进行比较.
图5为在109个物种代谢网络的W数列三维视图,一个曲线图代表一个物种的W数列.此图直观展示了通过基于主成分分析和小波变换方法提取出的网络特征.该图表明,代谢网络在整体而言存在着某种共性(曲线表现出的趋势近似),而在局部又存在着一些差异,进而运用特征信号相似度的概念定量的阐述这种共性与差异,即根据W数列求它们的相似度.

图5 109个物种代谢网络的W数列三维视图Fig.5 WSeries of 109species metabolic networks
通过对109个物种的代谢网络与随机网络的相似度、109个物种的代谢网络在生物的三个进化阶段内外的相似度进行计算比较,可以得到以下结果:代谢网络与随机网络的相似度的平均值为0.359 8,方差为0.037 5;任意两个不同物种代谢网络之间相似度的平均值为0.693 5,方差为0.034 8.不同的物种代谢网络之间存在较高的相似性,而与随机网络的相似度比较低;方差值都很小,相似度都分布在平均值附近,异常值较少.说明生物代谢网络自身结构具有特异性.
同一进化阶段内的不同物种代谢网络之间相似度的平均值为0.884 5,方差为0.029 3,存在很高的相似度,说明生物代谢网络在短时间进化中具有一定的稳定性;不同进化阶段中的不同物种代谢网络之间相似度的平均值为0.583 3,方差为0.024 6,相似度相对较低,说明物种代谢网络在长时间进化中发生了有规律的改变.
分别从古细菌、细菌、真核生物三个进化阶段中各随机选取4个物种的代谢网络数据进行举例说明.表1为12个物种代谢网络与3组随机网络的相似度比较,表2为12个物种代谢网络之间的相似度比较.
由比较结果分析可以证明,本章提出的方法可以将代谢网络与随机网络区分开;还可以用于判断某一物种大致所属的进化阶段或者某一物种与哪个阶段的模式生物在进化过程中比较接近,对代谢网络的进化研究起到一定的辅助作用,方便生物学家做进一步研究.
5.2 与集合论方法比较分析
在基于整体网络比较策略中,集合论的方法是用Jaccard距离来确定生物网络的进化距离[8].本章的MWD方法可以得到物种间的相似度rW,W*.物种的相似度和物种间的距离,本身的度量单位不同.实际中的距离表示两物体间相距的远近,这里物种间的距离概念指两物种间相似程度的区别,则相似程度小则距离大,相似程度大的则距离小.故可根据需要,将距离与相似度进行相互转换.将rW,W*转换成JB的计算公式如公式(14)所示.
定义9 物种间的距离JB指在两物种相似程度上的区别.根据定义8,相似度rW,W*本质上是两个向量的内积(余弦值),而物种间的距离JB本质上是向量之间的夹角,也就是两物种分离开的程度即角度越大,距离越大,反之角度越小距离越小.将rW,W*转换成JB的计算公式如下:


表1 12个物种代谢网络与3组随机网络的相似度比较Tab.1 Similarity between 12species metabolic networks and 3random networks

表2 12个物种三个进化阶段的物种代谢网络之间的相似度比较Tab.2 Similarity of 12species metabolic networks in three evolutionary stages
以公认的RNA距离[20]作为参考值,大肠杆菌E.coli为模式生物,将MWD方法计算出来的73个物种和模式生物的距离JB与用集合论的方法计算出来的Jaccard距离进行比较.
首先选取文献[20]中涉及的73个物种(共62种细菌和11种古细菌),根据其与大肠杆菌的RNA距离,将其有序排列;其次,用基于集合论方法计算73个物种与E.coli系统层酶图之间的进化距离即Jaccard距离,记为JC;用基于本章的MWD方法,计算73个物种与E.coli系统层酶图之间的相似度,转换为物种间的距离,记为JB;最后,以RNA距离为参考,将JB与JC进行比较,如表3和图6所示.

表3 与RNA距离误差的均值和标准差Tab.3 The mean and standard deviation of the error with RNA-distanse
表3列出了JC和JB与RNA距离之间误差的均值与标准差,以数值的形式对比较结果进行显示.与JC相比,JB具有更小的平均误差,直观地说明了本方法推算出进化距离的合理性.

图6 以RNA距离为参考,JC与JB的比较结果图Fig.6 The comparison of JC,JB and RNA-distance
分析JB与JC根据RNA距离的物种排序画出的曲线比较结果,如图6所示(x轴轴坐标分别对应73个物种按RNA距离的顺序排列,y轴对应的物种间的距离).图中带方块实线表示作为参考的RNA距离,带圈实线表示JC,带星实线表示JB.从直观上显示,本方法推算出的进化距离比Jaccard距离更接近参考值.但是,曲线尾部虽然呈上升趋势,其值比RNA小很多,反应出一些问题:
MWD方法本身进行了主成分分析、小波处理,提取出的特征信号,最后仅得出一个数值,大大压缩了网络信息量,数据可能失真.
小波低频滤波保留了大部分的平稳信号,波动大的奇异点被滤掉了,而这些点往往是区别不相似的地方.所以方法本身对相似度大的测得准,相似度小的测得不准,所以距离大的波动大,曲线尾部趋势不明显.
定义9中JB的定义方法只是简单直观地从余弦求夹角,是否还可以找到更合理的定义方法还有待进一步研究.
生物数据本身不足,一个物种普遍只有几百个节点,数据基础不足.
当然不排除作为参考的RNA距离本身也存在着误差.
综上所述,用MWD算法来比较两物种的网络,可以很好地表现出网络之间的相似度.但是用来测量两物种间的距离,相似度高的可以得到很好的效果,不过相似度低的物种之间的距离不能很好地表现,还有待进一步研究.
6 结 论
本章提出的基于主成分分析和小波变换的代谢网络比较方法,首次结合基于主成分分析方法分析代谢网络的拓扑结构属性,将小波分析运用于代谢网络的进化距离分析中.该方法能有效地分析不同物种代谢网络结构的相似程度,以揭示代谢网络的物种特异性,为代谢网络的进化研究提供数学基础;并且能够通过比较其相似性,较有效地区分不同进化阶段物种的代谢网络,可以对不同进化阶段的代谢网络的区分提供参考作用,探索进化规律;运用该方法将某物种的代谢网络与模式物种代谢网络的距离进行比较,发现该方法适用于推算相似度较高的网络距离,而对相似度较低的网络距离效果不明显.
[1] MA H,ZENG A P.Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms[J].Bioinformatics,2003,19(2):270-277.
[2] ZHOU Ting-ting,YUNG Kin-fung.MetaGen:apromising tool for modeling metabolic networks from KEGG [J].Progress in Biochemistry and Biophysics,2010,37(1):63-68.
[3] FORST C V,SCHULTEN K.Phylogenetic analysis of metabolic pathways[J].Journal of Molecular Evolution,2001,52(6):471-489.
[4] PINTER R Y,ROKHLENKO O,YEGER-LOTEM E,etal.A-lignment of metabolic pathways[J].Bioinformatics,2005,21(16):3401-3408.
[5] Oh S J,JOUNG J G,CHANG J H,etal.Construction of phylogenetic trees by kernel-based comparative analysis of metabolic networks[J].BMC Bioinformatics,2006,7:284.
[6] AGUILAR D,AVILES F X,QUEROL E,etal.Analysis of phenetic trees based on metabolic capabilites across the three domains of life[J].Journal of Molecular Biology,2004,340(3):491-512.
[7] MA H W,ZENG A P.Phylogenetic comparison of metabolic capacities of organisms at genome level[J].Molecular Phylogenetics and E-volution,2004,31(1):204-213.
[8] FORST C V,FLAMM C,HOFACKER I L,etal.Algebraic comparison of metabolic networks,phylogenetic inference,and metabolic innovation[J].BMC Bioinformatics,2006,7(1):67.
[9] TOHSATO Y.A method for species comparison of metabolic networks using reaction profile[J].IPSJ Digital Courier,2006,2:685-690.
[10] ZHOU Ting-ting,KEITH C C Chan,PAN Yi,etal.An approach for determining evolutionary distance in network-based phylogenetic analysis[J].Bioinformatics Research and Applications Lecture Notes in Computer Science,2008,4983:38-49.
[11] JEONG H,MASON S,BARABÁSI A L,etal.Lethality and centrality in protein networks[J].Nature,2001,411(6833):41-42.
[12] WATTS D J,STROGATZ S H.Collective dynamics of“smallworld”networks[J].Nature,1998,393:440-442.
[13] JOY M,BROCK A,INGBER D E,etal.High-betweenness proteins in the yeast protein interaction network[J].Journal of Biomedicine and Biotechnology,2005,2005(2):96-103.
[14] WUCHTY S,STADLER P F.Centers of complex networks[J].Journal of Theoretical Biology,2003,223(1):45-53.
[15] STEVENSON K,ZELEN M.Rethinking centrality:methods and examples[J].Social Networks,1989,11(1):1-37.
[16] ESTRADA E,RODRÍGUEZ-VELÁZQUEZ J A.Subgraph centrality in complex networks[J].Phys Rev E,2005,71(5),056103.
[17] BONACICH P F.Power and centrality:a family of measures[J].A-merican Journal of Sociology,1987,92(5):1170-1182.
[18] 陈峰.主成分回归分析[J].中国卫生统计,1991,8(1):20-22.CHEN Feng.Principal component regression analysis[J].Chinese Journal of Health Statistics,1991,8(1):20-22.(In Chinese)
[19] DAUBCHIES I.Orthonormal bases of compactly supported wavelets[J].Communications on Pure and Applied Mathematics,1988,41(7):909-996.
[20] ZHANG Y,ZHANG Z,LING L,etal.Conservation analysis of small RNA genes in escherichia coli[J].Bioinformatics,2004,20(5):599-603.
