哈尔滨市农民专业合作社运营效率评价

刘晓旭 孙国朋

（东北农业大学经济管理学院 黑龙江 哈尔滨 150000；）

1.前言

发达国家近现代农业发展历史表明,农民专业合作社可以有效提高农民的组织化程度，解决单一农户抵抗市场风险能力低下，经营和销售困难的问题。农民专业合作社对于增加农民收入，促进经济社会可持续发展具有明显的作用。

基于我国农民专业合作社事业快速发展，笔者在分析可能影响农民专业合作社发展运营效率因素的基础上，以哈尔滨市及其周边地区农民专业合作社为调查对象，以寻找农民专业合作社运营效率高低的影响因素并且综合评价哈尔滨市农民专业合作社运营效率为目的，针对本课题进行了研究。

2.运营效率的定义

农民专业合作社是以家庭承包经营为基础，由从事同类农产品生产经营的农民自愿组织起来，在技术、信息、资金、购销、加工、贮运等环节开展互助合作的经济组织。它以服务成员为宗旨，以维护成员利益为主要目的，是市场经济条件下，农民进行自我服务、自我发展、自我保护的一种行之有效的组织形式。

笔者对于农民专业合作社的运营效率是这样定义的：农民专业合作社的运营效率即农民专业合作社综合状况的反映，包括农民专业合作社社员的状况，农民专业合作社管理状况，农民专业合作社的发展运营状况。农民专业合作社运营效率的涵义也包含相应的外部环境，包括法律制度是否健全，政府对于合作社的财政与政策支持力度，以及农民对于合作社的评价与满意度状况。可以简单理解为农民专业合作社运营的健康值和管理水平的打分值。

3.影响农民专业合作社运营效率的因素

3.1 合作社社员状况

社员状况是已加入合作社的农民的个人以及家庭状况的全面反映，包括社员的性别、年龄、学历、年收入、务农收入、对合作社了解情况、加入合作社的动因共7个指标。

3.2 合作社财务状况

合作社财务状况是合作社盈利能力以及社员在合作社中所投入资金状况的反映，包括合作社是否有分红、社员加入合作社之后是否获得收益、社员在合作社中所投入资金占家庭存款比例三个指标。

3.3 合作社管理状况

合作社的管理状况是指合作社管理的科学化程度以及透明度的综合反映，包括合作社决策制度、社员参与管理程度、民主管理程度、财务公开度四个指标。

3.4 社员满意度情况

社员满意度状况指的是社员对合作社以及相关服务与支持的满意度，包括社员对所在合作社满意度、社员对合作社提供服务是否满意、对政府支持满意程度4个指标。

4.数据获得与处理

4.1 数据获得

根据所选取的可能影响合作社运营效率的因素，在黑龙江省哈尔滨市及其周边地区选择了六家合作社进行重点调查。调查共分三部分：一是访谈形式走访合作社所在地村委会以及相关政府部门，获取当地关于农民专业合作社方面的政策措施以及相关方面的信息；二是通过与农民专业合作社社长的交谈，了解各个合作社具体的管理措施与发展现状；三是入户调查的形式与农户（既包括社员也包括非社员）的交流，了解他们的个人特征、家庭情况以及收入状况。通过访谈及问卷的形式对哈尔滨市农民合作社事业发展现状进行全面的了解。共调查农民专业合作社6个，发放问卷174份，收回149份，其中有效问卷118份。

4.2 变量选取

根据调查问卷统计结果共选取了合作社社员状况，合作社财务状况，合作社管理状况，社员满意度情况四类指标。其中社员状况包括：年龄、学历、务农收入。合作社财务状况包括：合作社是否有分红、在合作社所投入资金占家庭存款比例、社员入社是否获得收益。合作社管理状况包括：合作社决策制度、社员参与管理程度、民主管理程度、财务公开度。社员满意度包括：社员对所在合作社服务满意程度、对政府支持满意程度。共12个指标作为影响合作社运营效率的因素进行分析。

4.3 数据处理

将调查问卷进行统计之后，有32组数据是可用的，分别代表了32个典型的调查对象。对于实证调查所得数据进行如下处理：首先将每个变量所对应的选项按照 0、1、2、3、4、5 的顺序进行标记。例如，对于学历这一变量未上学、小学、初中、高中、大学及以上，分别对应的值就是 1、2、3、4、5。

5.模型建立

5.1 模型思路

在本文中将采用三个模型的综合对问题进行求解，即通过TOPSIS法进行数据的处理，通过多元线性回归分析进行满意度的分析，最后通过层次分析法（AHP）进行综合评价排序，从而得到哈尔滨市农民专业合作社的定量评价结果

（1）首先将运用TOPSIS法的思想将数据进行处理，设立打分规则，将评价模型中将要用到的变量值转换成按照百分制进行打分的比较值，打分较高对于运营效率将有着较高的正向影响。

（2）然后通过满意度将32个数据进行分类，建立对于合作社满意度的多元线性回归模型，分别求得32个人的满意度。再将32个人分为非常不满意、不满意、比较满意、满意、非常满意五类，通过TOPSIS法中的思想分别求得五类人的加权评分结果。

（3）最后通过四类指标构造准则层判断矩阵，通过五类人的百分制打分值构造评分层判断矩阵，运用AHP根据分别得到的排序结果进行综合评判排序，再根据综合评判排序结果进行加权运算得到最后的综合评价值。

5.2 TO PSS处理

（1）构建百分制矩阵。表4中的数据是按照变量对应选项赋值得到的统计结果，例如对于社员状况中的学历来讲，未上学对应的赋值为20分，小学对应的赋值为40，初中对应的赋值为60，高中对应的赋值为80，大学及以上对应的赋值为100，依此类推就得到了对于12个变量的百分制打分值。

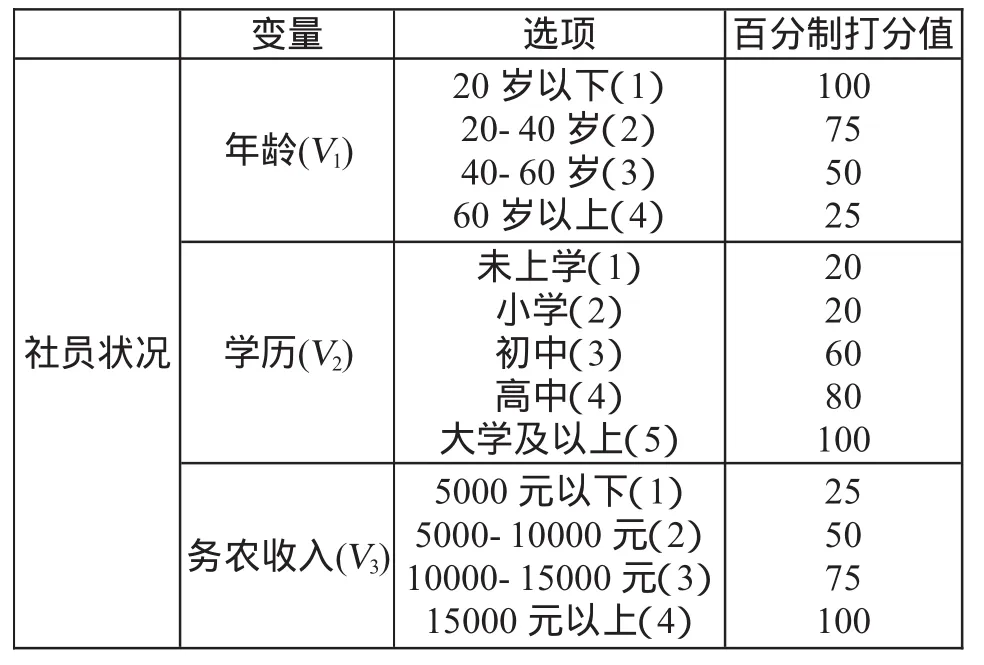
表1 变量赋值百分制表

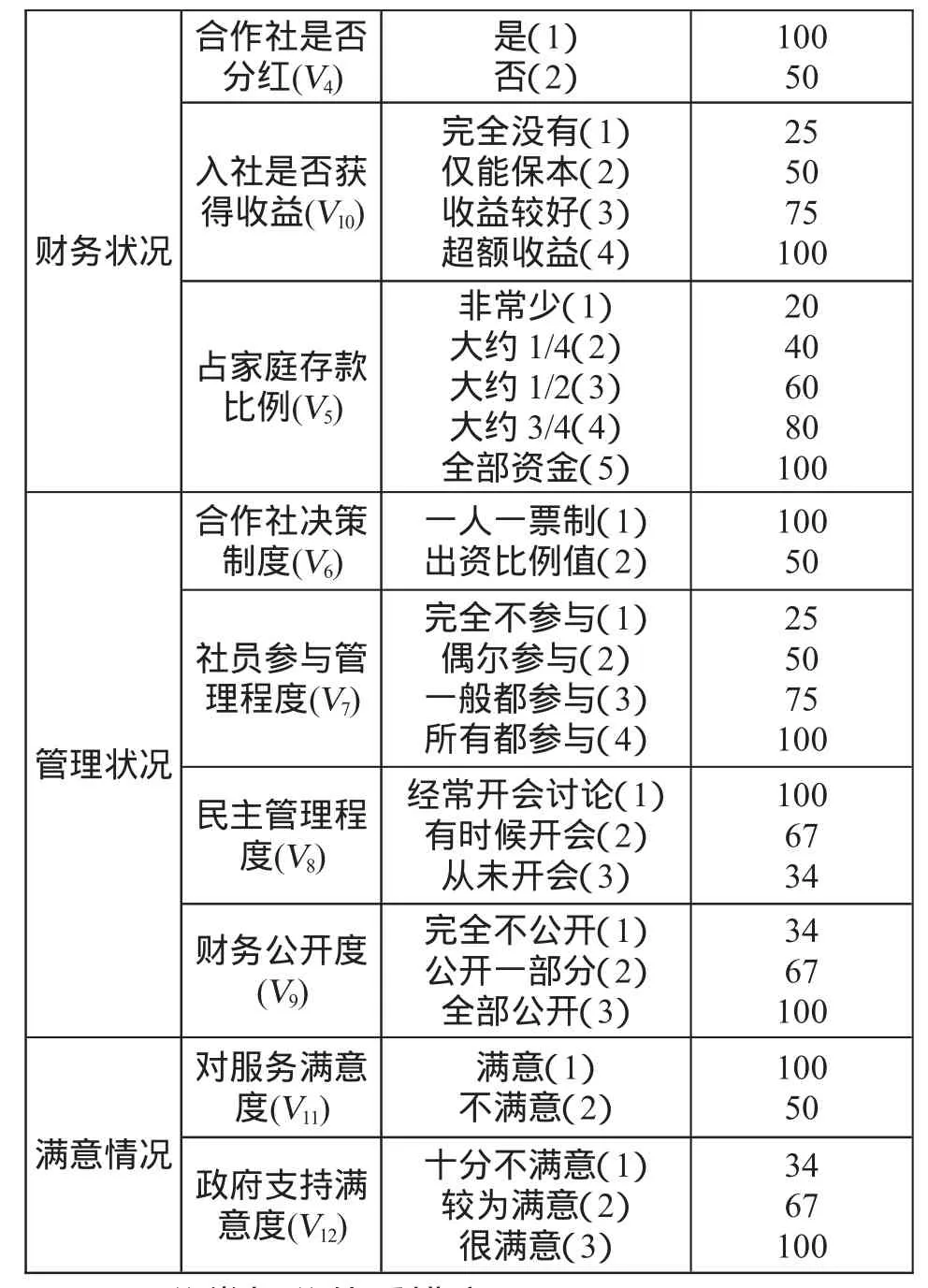
合作社是否10050完全没有（1）仅能保本（2）收益较好（3）超额收益（4）分红(V4)是（1）否（2）入社是否获得收益(V10)财务状况25507510020406080100占家庭存款比例(V5)合作社决策10050社员参与管理程度(V7)非常少（1）大约 1/4（2）大约 1/2（3）大约 3/4（4）全部资金（5）管理状况完全不参与（1）偶尔参与（2）一般都参与（3）所有都参与（4）制度(V6)一人一票制（1）出资比例值（2）2550751001006734财务公开度(V9)民主管理程度(V8)完全不公开（1）公开一部分（2）全部公开（3）经常开会讨论（1）有时候开会（2）从未开会（3）3467100对服务满意度(V11)满意（1）不满意（2）10050满意情况 政府支持满意度(V12)十分不满意（1）较为满意（2）很满意（3）3467100

（2）分类打分值重排序

对于加入合作社的社员来讲，能够获得收益就会对合作社较为满意，所以重新定义社员对合作社满意情况。处理办法如下：对于完全没有收益和入社之后仅能保本的社员认为其没有收益，对于收益较好和能够获得超额收益的定义为能够获得收益，凡是定义为能够获得收益或者是对于合作社提供的服务满意的就认为该社员对其所在合作社是满意的。

6.满意度计算

6.1 多元线性回归分析

本文中对满意度选取的模型为多元线性回归模型，则模型的方程为：

y=β+α1x1+α2x2+α3x3+α4x4+α5x5+α6x6+α7x7+α8x8+α9x9+α10x10+α11x11

选取对合作社满意与否为因变量，剩余的11个变量为自变量，建立多元线性回归模型计算32个社员的满意度情况。将MATLAB 7.0运算所得的表5中的数据代入spss 13.0中，运用enter法让所有自变量均进入方程，V11作为Dependent，其余11个变量作为Independent，分析所得结果如图1。

由图10可以看出模型的决定系数为0.812，决定系数较高。由图11可以看出模型P=0.000，具有统计学意义，模型符合要求。

由图12中数据可以看出社员对合作社满意度的影响因素中影响最大的是社员加入合作社之后是否有收益，其次是对政府支持的满意情况，然后是在合作社中投入的资金占家庭存款的比例。社员最为关心的还是加入合作社之后是否能够获得现实收益。根据图12中数据得到多元线性回归模型为：

图1 模型决定系数

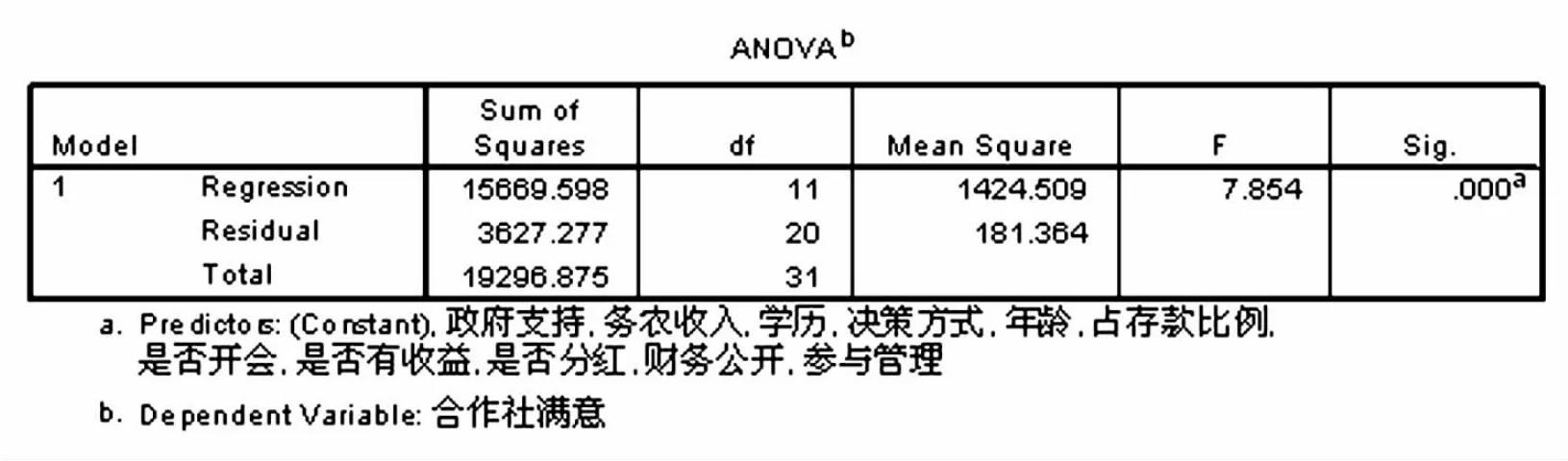
图2 模型检验

图3 变量系数

y=-31.531-0.243x1+0.008x2+0.059x3+0.114x4+0.779x5+0.229x6+0.119x7+0.287x8-0.048x9-0.097x10+0.475x11

根据多元线性回归分析模型计算32人的满意度结果见表2。

表2中数据既是所求的32个人对于其所在合作社的满意度。需要注意的是所求得的满意度仅是为了对32人进行分类，所求数据并不参与AHP模型的运算。

6.2 满意度分类流程

（1）首先运用MATLAB 7.0通过极差变换将满意度进行规范化处理，使得满意度变为之间的数值。

其中r值为满意度百分制打分值，X值为规范化之后的0-1之间的数值。

（2）定义X≤0.2的为非常不满意；0.2＜X≤0.4为不满意；0.4＜X≤0.6为比较满意；0.6＜X≤0.8为满意；0.8＜X≤1为非常满意。

（3）非常不满意用数字1来表示，不满意用数字2来表示，比较满意用数字3来表示，满意用数字4来表示，非常满意用数字5来表示。这五类人就是满意度从低到高的五个分类。

7.综合评价排序

7.1 准则层计算过程

7.1.1 构造准则层判断矩阵

（1）在定义准则层判断矩阵时，按照每一类指标所拥有指标的个数作为彼此重要性的判断依据。则准则层W1=3W1=3，W2=3，W3=4，W4=2。

（2）构造判断矩阵A

则准则层判断矩阵为：

表2 社员满意度表

7.1.2 准则层排序

（1）首先进行列标准化，即准则层判断矩阵的每个元素除以所在列的和

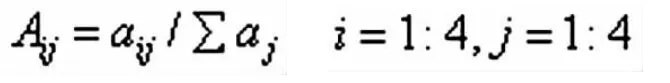
（2）然后每一行求出平均值所得到的向量即为特征向量

（3）最后求得准则层的排序结果为

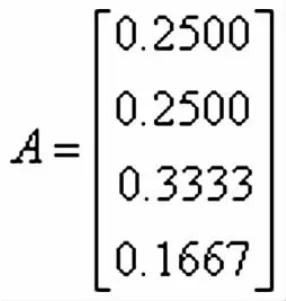
7.1.3 一致性检验

（1）首先进行一致性检验，计算CI

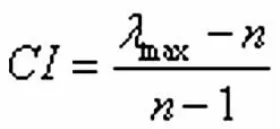
（2）然后再计算一致性比率CR

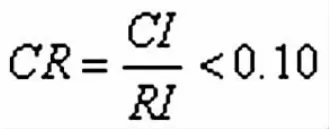
矩阵阶数 1 2 3 4 5 6 7 8 9 10 11 RI 0 0 0.580.91.121.241.321.411.451.491.51

7.2 方案层计算过程

7.2.1 构造准则层判断矩阵

（1）首先提取五类满意度的百分制打分表中的数据，分别构造各自的矩阵。非常不满意为B1，不满意为B2，比较满意为B3，满意为B4，非常满意为B5

（2）运用TOPSIS法思想，对每个矩阵进行加总平均，首先将所有行加到一起

（3）最后将得到的B1，B2，B3，B4，B5按照列构造为新的矩阵Bi，Bi，i=1:5中的数据就是五类满意度的人在12种指标上的百分制打分值。将按照四类指标进行加和。将1、2、3列加总得到五种满意度的社员个人状况得分值，4、5、6列加总得到五种满意度合作社财务状况得分值，7、8、9、10列加总得到五种满意度合作社管理状况得分值，11、12列加总得到社员满意情况得分值。

（4）分别计算四类指标的判断矩阵，以第一列为例。首先提取矩阵B第一列，分别构造两个矩阵B11，B12。则方案层合作社个人情况的判断矩阵B1等于B11除以B12对应位置的元素，所得到的四个矩阵B1，B2，B3，B4就是四个准则的判断矩阵。

7.2.2 方案层排序

（1）依照准则层计算方法来计算方案层的排序，以社员个人状况为例。首先进行列标准化，即准则层判断矩阵的每个元素除以所在列的和

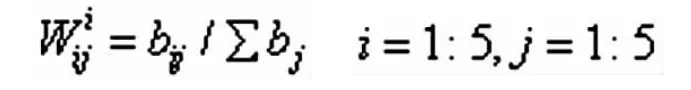
（2）然后每一行求出平均值所得到的向量即为特征向量

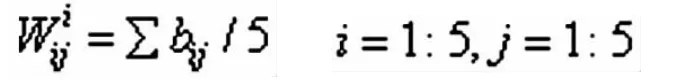
（3）最后求得社员个人状况的排序结果

7.2.3 一致性检验

（1）以社员个人状况为例，按照准则层一致性检验的办法，首先进行一致性检验，计算CI。通过MATLAB 7.0进行分解，求得最大特征值求得从而计算CI。CI=0。方案层社员个人状况通过一致性检验。

（2）然后再计算一致性比率CR

（3）通过对其他三个方案层的计算，CI=0，CR＜0.10所以均通过一致性检验。

7.3 综合评价排序

最后进行的是五个满意度的总排序，计算综合得分W

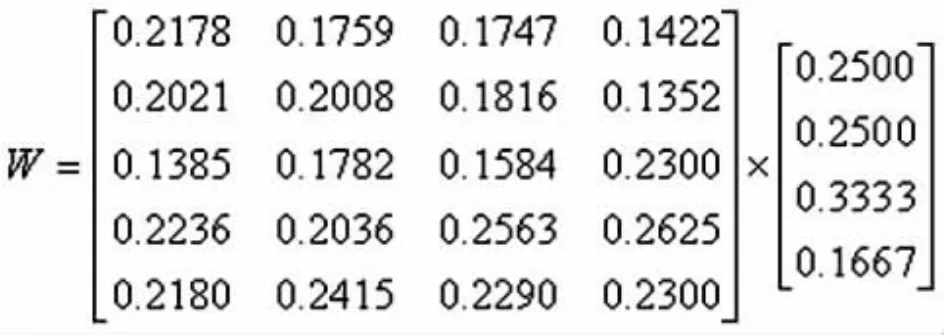
最终的计算结果五类满意度的综合效率得分为：

8.结论

由W可以看出，五类满意度，非常不满意、不满意、比较满意、满意、非常满意的效率得分分别为：0.18040.18380.17030.23600.2295。总的趋势是由低到高，参照线性回归分析模型中对满意度由低到高的定义，效率评判排序结果对满意度拟合的相当优秀。

为了计算合作社运营效率的综合评价得分，首先将W由小到大排序。按照效率评分高低设立百分制打分原则wt，因为即使合作社运营较差，拥有固定的办公地点，形式上健全的组织机构，所以则排序中运营效率最低的得分为并不为0定义为40分，最高的为100分。

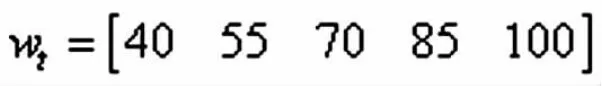
初步百分制评分为WT为W乘以wt的转制对应位置元素

在进行满意度分类时五类满意度的人数分别为[12 7 1 7 5]，因为已经根据效率得分对W进行了调整，所以对效率的权重系数进行相应顺序的调整w为：

计算总体效率得分时要加上此权重，首先将权重矩阵规范化

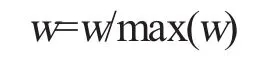
规范化之后的权重系数w为：

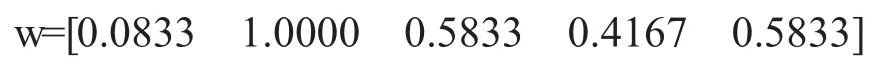
将W与权重系数矩阵的转置相乘就是哈尔滨市农民专业合作社运营效率的加权得分值WTT：

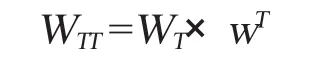
运用matlab求得，WTT=39.8887。哈尔滨市农民专业合作社依照百分制打分原则最终评价结果为40分，哈尔滨市农民专业合作社事业发展现状亟待改善。