基于利用回归分析法预报上下游相关洪峰水位

2011-08-13郭锐

黑龙江水利科技 2011年4期

郭锐

(黑河水文局，黑龙江黑河164300)

目前，在一些无流量控制站的流域，一般采用上下游洪峰相关水位图来进行短期洪水预报工作。上下游相关洪峰水位预报法属最基本也是最原始的水文预报技术手段之一，该方法的优点是使用简便且通俗易懂，不足之处是相关图制作过程比较繁琐，尤其是在有多个预报因子影响时还存在无法合理定线的问题。相关图在绘制和实际使用时还存在人为主观任意性较大的弊端。采用回归方程的近似函数来表达上下游洪峰水位关系与使用相关图法相比较，具有明显的理论性强、预报精度高、工作流程短，便于计算机处理，方便、快捷的优点。本文通过对黑龙江奇克站(上游)与乌云站(下游)洪峰水位实例数据来说明回归方程法在上下游洪峰相关水位预报过程中的应用。

1 回归分析简介

回归分析是确定两种或两种以上变数间相互依赖关系的一种统计分析方法，应用十分广泛。回归分析按照涉及自变量的多少，可分为一元回归分析和多元回归分析，常用数学方程来表述。如果在回归分析中只包括一个自变量和一个因变量，且二者的关系可用一条直线来近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。“线性”与“非线性”，常用于区别函数y=f(x)对自变量x的依赖关系。线性函数即一次函数，符合叠加原理且变量间的函数关系是直线，其它函数则为非线性函数，函数图像不呈直线状态。

2 实例应用分析

2.1 采用数据与预报要求

根据分别在黑龙江中游段奇克站与乌云站选定的40场较大洪水的洪峰水位、相应同时水位和洪峰传播时间数据，按照河道上下游相应洪峰水位预报原理和要求，选定相关系数较高的预报因子，对乌云站的洪峰水位和洪水传播时间进行拟合预报。洪峰水位预报的允许误差按水位变幅来确定，最大变幅的样本数据，其预报允许误差为变幅均方差δ，变幅最小的按0.3δ来控制(最小允许误差限定为0.10 m)，其余样本数据的许可误差按上述两值所确定的直线用内插法求出。洪峰传播时间预报的允许误差用小于洪峰实际传播时间的30%(最小允许误差为3 h)来控制。拟合预报的整体项目精度按《水文情报预报规范》的要求来确定。

2.2 回归方程建立

首先点绘各预报因子与预报项目的关系点据图，由图1、图2中趋势线可见，乌云站洪峰水位分别与上游奇克站洪峰水位和奇克站洪峰时乌云站同时水位呈近似直线关系，相关系数分别为0.97和0.98。黑龙江奇克站洪峰水位与奇克～乌云站洪峰传播时间呈近似幂函数曲线关系，相关系数为0.71。因此，乌云站洪峰水位采用奇克站洪峰水位和奇克站洪峰时乌云站同时水位作为预报因子以二元线性回归方程的形式来进行历史拟合预报，预报方程为y=k1x1+k2x2+c，上式中y为乌云站预报洪峰水位，x1为奇克站洪峰水位，x2为奇克站洪峰时乌云站同时水位，c为常数项，k1、k2为方程系数。奇克站～乌云站洪峰传播时间以奇克站洪峰水位为预报因子建立非线性回归方程来进行历史拟合预报，本文采用目前普遍使用的三参数幂函数(y=axb+c)线型，即y=atb+c，经公式变换可得上式中t为奇克站～乌云站洪峰传播时间，y为奇克站洪峰水位，a、b、c为方程系数，d项是为提高方程拟合精度而补充加入的常数项。

图1 黑龙江奇克站乌云站洪峰水位趋势线图

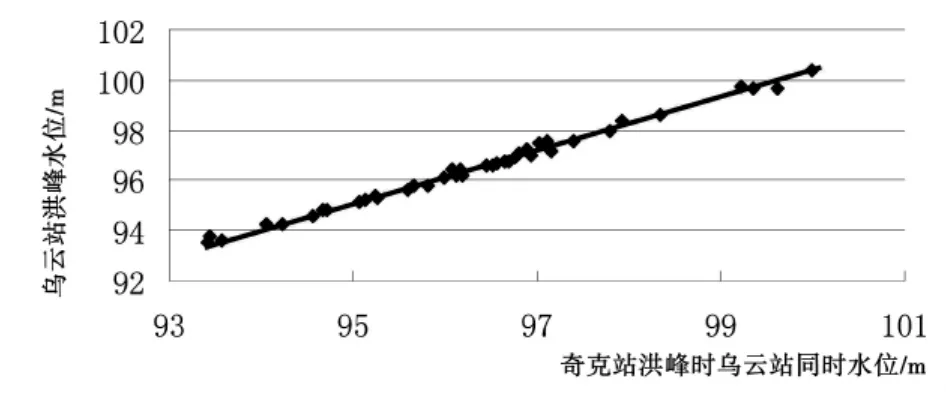
图2 黑龙江乌云站同时水位与洪峰水位趋势线图

图3 黑龙江奇克站洪峰水位奇克～乌云站洪峰传播时间趋势线图

2.3 历史数据拟合预报及精度检验

根据选定的样本系列数据，按照上述回归方程的形式以最小二乘法为回归计算约束标准，得出乌云站洪峰水位和洪峰传播时间预报方程，即 Y=0.04483X1+0.98868X2－3.08291和回归计算结果和检验结果见表1、表2。经统计，采用相关图法和回归方程法进行洪峰水位拟合预报的合格率分别为70%和73%，达到乙级预报项目标准，洪峰传播时间预报的合格率分别为62%和65%，达到丙级预报项目标准，回归方程法拟合结果略高于相关图法，能够满足实际使用需要。

3 结语

回归方程在实际应用时应注意使用环境的变化，当预报影响因子个数有变动时，应及时确定更新方程形式，重新率定方程系数，否则会带来较大的计算误差。由于天然洪水演变过程具备较强的随机性和不确定性，任何数学模型都无法全面准确地模拟洪水变化过程，在实际洪水预报工作中只能做为必要的参考手段之一来应用。由于受实测资料范围的限制，回归方程所选用的预报因子较少，洪峰传播时间预报方程所采用的时间值与水位值还存在数值类型不一致和相关系数较低的问题，二者只是在具体数值统计上具有一定的函数关系，缺少足够的理论支撑，因此回归方程拟合精度不是很高，还有待进一步完善提高。