基于熵权的模糊综合评价模型的土壤等级评价中的应用

刘 迪，马占岳

(黑龙江省水利科学研究院，哈尔滨150080)

近年来，由于土地开发和植被破坏导致水土流失等土壤破坏行为的越来越严重，因此土壤等级评价也越来越受到人们重视。土壤的质量的等级是一个地区土壤水平的重要体现，土壤质量是土壤特性的综合反映，也是揭示土壤条件动态的最敏感的指标［1］，土壤质量可以体现人类活动对土壤的影响，对一个地区的土壤做出适宜的分类与评价，对这个地区的农业生产、防治水土流失等活动有重要的影响。现在，在土壤环境质量的评价方面，为便于规范化管理和增加可比性，参照我国绿色食品发展中心于2001年发布实施的绿色食品产地环境质量现状评价技术原则进行评价，评价方法采用单因子污染指数法和综合污染指数法［2］。对于土壤环境质量等级的评价方法，还有统一的见解。模糊综合评价是一种应用广泛的数据处理方法［3－4］，本文提出用基于熵权的模糊综合评价方法对土壤等级进行评价。

1 模糊综合评价的方法和步骤

设评价因子集合为:u= {u1，u2，…un}，其中u1，u2，…，un为参与评价的n个评价因子.设评价等级集合为:v={v1，v2，…，vm}，其中v1，v2，…，vm为m个评价等级。

1.1 数据归一化处理

对于越大越优的指标:

对于越小越优的指标:

式中:xmax(j)为第j个指标值的最大值;xmin(j)为第j个指标值的最小值;x(i，j)为指标特征值归一化的序列;x*(i，j)为第i个样本的第j个指标值。

1.2 建立单因素评判矩阵

建立单因素评判矩阵，即:

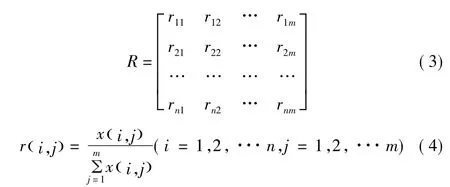
式中:rij表示按第i个评价指标xi进行评价时，ui属于第j个评价类vj的测度值，其大小表示样本的优劣程度。

1.3 权重计算

利用上述归一化处理的矩阵，计算第i个评价指标下第j个待评价监测点评价指标特征值比重:

计算第i个评价指标的熵:

计算第i个评价指标的权重:

1.4 综合评判

对于权重 A= (a1，a2，…，an)，取max－min合成运算，即用模型M(∧，∨ ) 计算B=A·R，具体如下:

2 实例研究

2.1 基础数据

根据文献，以某地区的土壤质量评价为例，选择文献中的一组原始数据，见表1，利用基于熵权的模糊综合评价模型对该原始数据进行处理分析，对土壤等级进行评价。

表1 各项指标的原始数据表

2.2 评价过程

2.2.1 建立评价矩阵

根据原始数据，选择评价指标，并根据原始数据建立如下特征值矩阵:

2.2.2 归一化处理

利用公式(1)和(2)对原始评价矩阵中的数据进行归一化处理，建立归一化单因素评价指标矩阵R:

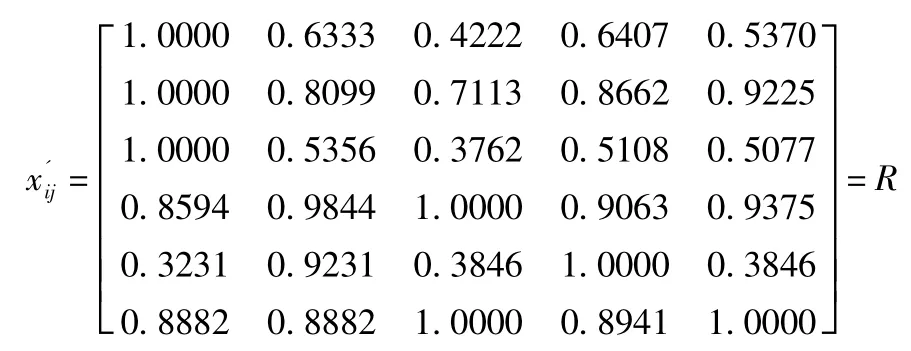
2.2.3 熵权法计算权重

2.2.3.1 求解特征值比重矩阵

利用公式(4)和上述步骤中得到的归一化评价指标矩阵可以得到特征值比重矩阵pij。

2.2.3.2 计算各评价指标的熵

利用公式(5)计算可得各指标的熵:

2.2.3.3 计算各指标的权重

利用公式(6)计算可得各指标的权重:

2.2.4 综合评价

对于权重，取max－min合成运算:

2.3 评价结果及其分析

根据综合评价得到的结果，可以对所选的5个样本土壤质量进行排序，即样本1＞样本2＞样本4＞样本5＞样本3。

3 结束语

本文介绍了模糊综合评判决策模型，其原理简单，计算快捷，具有一定的先进性和使用性。特别是在用于多指标评价中，能较好的反应出个指标间特性，是一种十分有效的多因素决策方法。另外通过熵权法与模糊综合评价的耦合，熵权法能够最大程度地挖掘数据本身的信息确定各指标的权重值，有效的解决了在模糊综合评价过程中关于权重主观性较强的缺点，使评价更加地客观。

［1］王喜林.加权系数法在土壤等级评价上的应用［J］.安徽农业科学:2010，38(31):17477－17478.

［2］田卫，俞穆清，张虎城，等.长春市城区三大品种秋菜无公害化产地筛选与环境质量评价［J］.东北师大学报:自然科学版，2003(12):82－87.

［3］付强.数据处理方法及其农业中的应用［M］.北京:科学出版社，2006.

［4］谢季坚，刘承平.模糊数学方法及其应用(第二版)［M］.武汉:华中科技大学出版社，2000.