数字基带预失真系统中环路延迟估计的FPGA实现

刘正平，夏 威，何子述

（电子科技大学 电子工程学院，四川 成都 611731）

随着现代无线通信产业的快速发展，为了充分利用有限的无线频谱资源，现代通信系统采用了正交调制和多载波技术。然而这些技术对发射端前置高功率放大器(HPA)的线性度提出了非常高的要求[1]。在功率回退技术、负反馈法、前馈线性化技术和数字预失真技术等常用的线性化技术中，数字基带预失真技术因其成本低廉而得到了广泛的应用[2]。

在基于查找表(LUT)数字基带预失真(DPD)系统[3]的实现过程中，DPD需要正确对比输入信号x(n)和功率放大器输出端的反馈信号z(n)。通常反馈信号相对于输入信号有一段时间延迟，这就破坏了预失真系统的稳定性，因此正确估计环路延迟并对其进行补偿就显得十分必要。

近年来，国内外学者对环路延迟估计进行了分析并提出了一些估计算法，如迭代法(Nagata Algorithm)[3]、延时锁定环路法(DLL Method)[4]和相关检测法(Correlation method)[5]等，它们都有各自的优缺点。 本文结合参考文献[6]提出的幅度差相关算法和参考文献[7]中基于数据流相关运算的改进算法提出了新的方法。该方法在用于FPGA实现时难度低于参考文献[6]，同时在信号失真的情况下也能给出正确的估计值。

1 环路延迟估计算法

环路延迟是指信号从系统输入端到反馈输出端所产生的时间延迟。通常，反馈信号z(n)相对于输入信号x(n)都会有一段时间的延迟，并且该延迟会随着时间和温度的改变而改变，故需要对其进行实时估计。

[6]提出的幅度差相关法为：

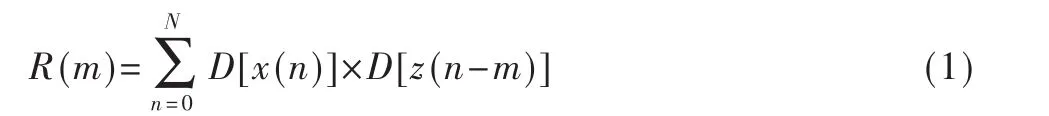
其中，N为采样数据长度，m为输入信号 x(n)与反馈信号 z(n)之间的时间差，取值范围为：m∈[0 N]，幅度差函数 D[·]的定义为：

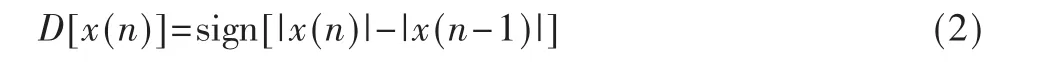
其中|x(n)|为信号的幅度，sign(·)的定义为：

算法通过搜索R(m)的最大值得到环路延迟的估计值。其通过对信号幅度的差取符号，减少了运算量。但用于FPGA实现时，需要复杂的时序控制，可实现度不高。

数据流相关运算的表达式为：

参考文献[7]根据数据流相关运算提出了改进算法，仅用减法器就可实现整数倍的延迟估计。其表达式为：

其中 Re(·)和 Im(·)分别表示取信号的实部和虚部，|·|表示取绝对值。

此算法通过误差的叠加尽量放大两信号之间的差异。当无整数倍延迟偏差时，两组数据差值最小，故可以通过搜索R(m)的最小值得到整数倍环路延迟的估计值。由式(5)可知此算法具有运算复杂度低和易于实现的优点，但它要求反馈信号未经衰落信道畸变及高斯噪声影响才可以实现。

针对上述两种算法的不足，本文提出了新的方法。其基本表达式为：

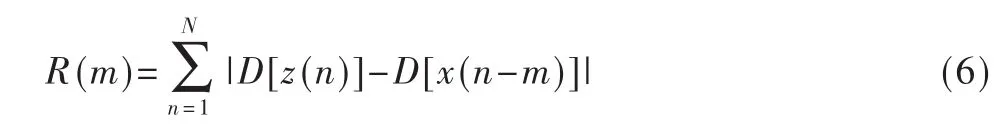
其中|·|表示取绝对值，其他符号的定义与参考文献[6]一致。

由PA输入、输出两组数据具有一定的相关性可知，当没有整数倍延迟偏差时，两组数据差值最小，故可以通过搜索R(m)的最小值得到整数倍环路延迟的估计值。

对比式(6)和式(1)可知，本方法在用于FPGA实现时比参考文献[7]要减少一个计算 D[x(n)]×D[z(n-m)]的步骤；同时本方法在计算时只涉及到加减运算，故其时序控制比参考文献[6]简单。对比式(6)和式(5)，本方法先通过式(2)保留信号的变化信息，再通过式(6)保留输入信号和反馈信号之间的相似性，故其不用像参考文献[7]那样对反馈信号有要求。不过，本方法和其他相关算法一样要求输入信号的周期必须大于环路延迟的值。

2 Matlab仿真结果及分析

为了验证本文所提方法的有效性，进行了仿真分析。仿真所采用的系统框图如图1所示，其中PA行为模型采用的是并行维纳结构，OFDM信号延迟了22个周期。

图1 仿真所用的系统框图

为了验证算法的鲁棒性，本文还给出了算法在反馈信号z(n)相对于输入信号x(n)失真不同程度的情况下，环路延迟估计值。其中，输入信号和反馈信号的功率谱密度如图2所示。反馈信号是输入信号经过PA后未加噪声、而加了SNR=30 dB和SNR=20 dB的高斯白噪声后得到的。图3所示为采用本文所提出的方法，对图2中的信号进行环路延迟估计给出的理论估计值。由图3可知，当反馈信号严重失真时，本文提出的方法也能给出正确的估计值，从而证明了本文所提方法的有效性。

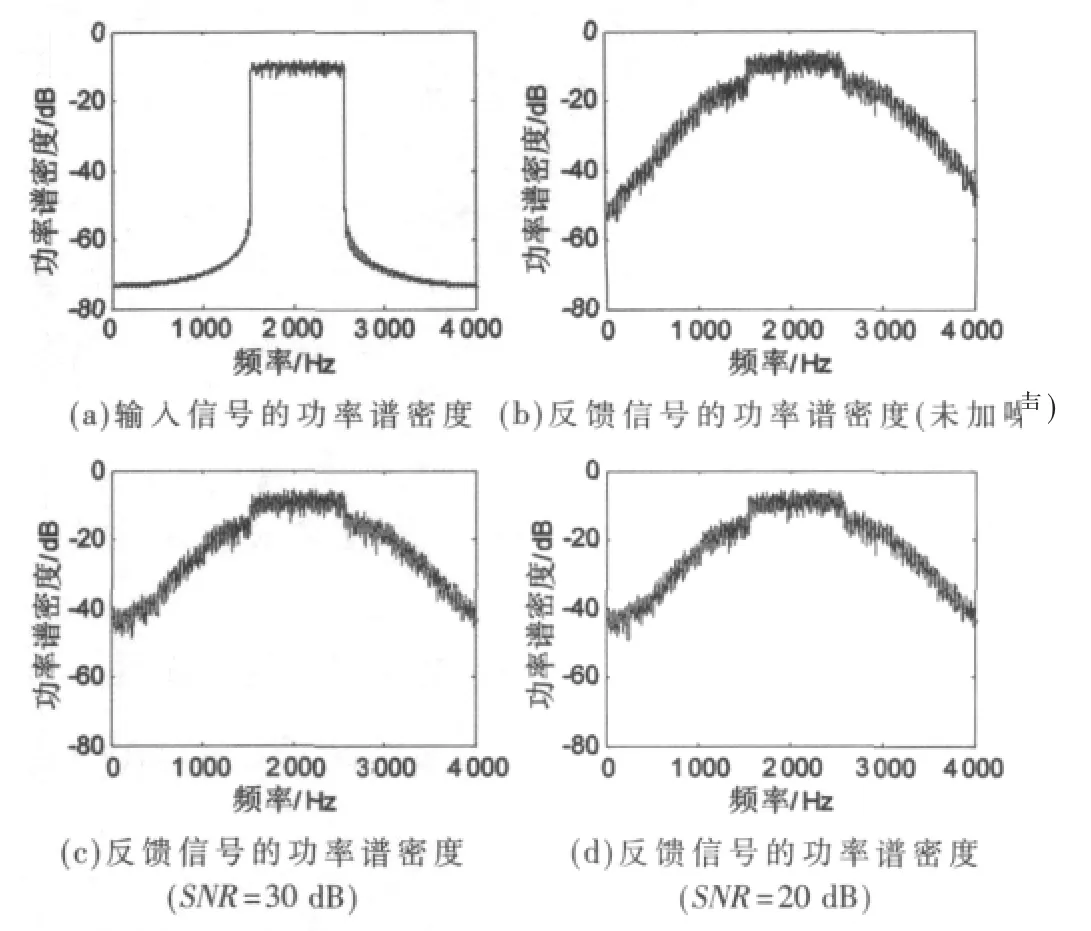
图2 输入信号和反馈信号的功率谱密度

图3 输入信号相同，PA输出信号不同的情况下，采用本文所提出的方法给出的估计值

3 环路延时估计的FPGA实现

根据实际数字基带预失真系统的需要，环路延时估计在采用FPGA芯片Stratix II EP2S60F672C4实现时，“相关窗”的长度 L取 250，共做了 60次相关即k∈(0，60)，其实现的结构框图如图4所示。

图4 整数倍环路延迟估计的实现结构图

(1)接收存储数据。将所要使用的数据存储在FPGA的RAM中，存储的数据包含基带发射信号及接收信号的实部、虚部4组数据。

(2)计算幅度差函数模块。由于使用信号幅度的平方代替幅度计算幅度差函数不改变幅度差函数D[·]的计算结果，同时FPGA中实现幅度的平方比幅度的复杂度更低，故本模块先根据式(7)计算出幅度的平方，再根据式(2)的变形式(8)计算幅度差函数D[·]的值。

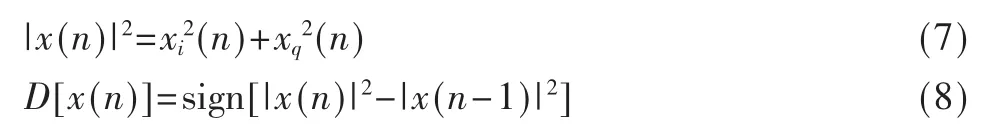
(3)计算幅度差函数的误差模块。本模块主要计算|D[xfb(n)]-D[xin(n-k)]|的值。

(4)计算相关模块。根据式(6)计算相关模块，其中L=250，k∈(0，60)。

(5)搜索最小项模块。本模块采用的是数据比对存储实现算法，即当输入的数据与前一个输入的数据相比较；存储较小的数据及其自变量m的值；60组数据比对完成后，存储在FPGA寄存器中的m值则是所要估计的整数倍环路延迟数目。

(6)数据流控制模块。本模块的目的是保证各个模块能按既定的顺序工作。

4 系统调试

为了验证所设计模块的正确性，本文对比了输入信号为八音信号且激发了PA的非线性的情况下，Matlab、Modelsim和Signal Tap II中整数倍环路延迟估计模块给出的估计值。其中Matlab中信号的功率谱密度图和延迟估计值如图5所示。

图5 PA输入和输出信号的功率谱和延迟估计值

将图5中的信号导入Modelsim SE 6.5c进行时序仿真，仿真结果如图6所示。对比图5、图6可知，本文所设计的实现方法是正确的。

最后把本文所设计的整数倍环路延迟估计模块加入到数字基带预失真系统中，进行系统测试。信号源所产生的信号功率谱如图5所示，在SignalTap II中抓取的结果如图7所示，由图可知，该模块的功能是正确的。

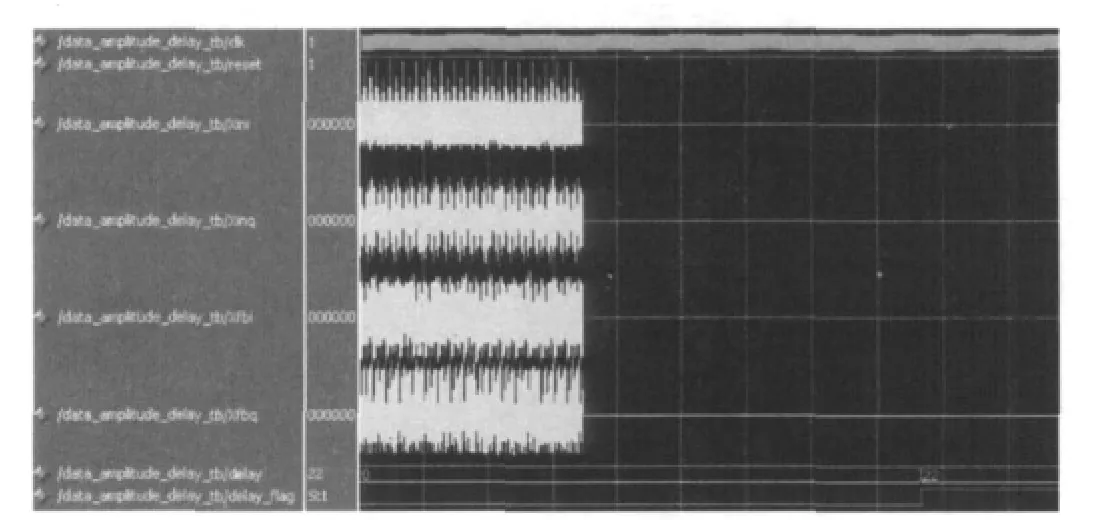
图6 Modelsim中的仿真结果

图7 SignalTap II中的仿真结果

本文针对数字基带预失真系统中的延迟估计问题，提出了一种易于FPGA实现的整数倍环路延迟估计的方法。由Matlab仿真结果可知，本文所提出的方法在信号失真的情况下能正确给出环路延时的估计值，从而证明了该方法的有效性。最后，基于FPGA芯片Stratix II EP2S60F672C4设计实现了整数倍环路延迟估计模块，由Modelsim SE 6.5c时序仿真和SignalTap II的硬件调试结果与Matlab理论仿真结果对比可知，该实现方法是可行的。本文设计的环路延迟估计模块已经应用于数字基带预失真系统。

参考文献

[1]AI B，YANG Z X，PAN C Y，et al.Improved LUT technique for HPA nonlinear pre-distortion in OFDM systems[J].Wireless Personal Communications(S0929-6212)，2006，38(4)：495-507.

[2]ANDING Z，DRAXLER P J，YAN J J，et al.Open-loop digital predistorter for RF power amplifiers using dynamic deviation reduction-based volterra series[J].Microwave Theory and Techniques[J]，IEEE Transactions on，2008，56(7)：1524-1534.

[3]NAGATA Y.Linear amplification technique for digital mobile communications[C].In Vehicular Technology Conference，IEEE 39th，1989.

[4]SHIGANG T，KE G，JUN W，et al.Loop delay correction for adaptive digital linearization of power amplifiers[C].In Wireless Communications and Networking Conference，WCNC 2007.

[5]RAWAT M，et al.Adaptive digital predistortion for power amplifiers with real time modeling of memoryless complex gains[R].US Parent，2002.

[6]LI H，KWON D H，CHEN D，et al.A fast digital predistortion algorithm for radio-frequency power amplifier linearization with loop delay compensation[J].IEEE Journal of Selected Topics in Signal Processing，2009，3(3)：374-383.

[7]艾渤，钟章队，朱刚，等.放大器预失真系统中的环路延迟估计[J].系统仿真学报，2007，19(19)：4487-4489.