基于模糊层次分析法的电力安全风险评估

2011-08-13钟银超谭世海杨太国

重庆电力高等专科学校学报 2011年5期

钟银超，谭世海，杨太国

(1.重庆市巫山县供电有限责任公司，重庆巫山404700;2.重庆电力高等专科学校，重庆400053)

0 引言

电力是国民经济的基础，关系到国民经济的发展和社会的进步。随着电力产业的不断改革，电力安全生产变得越来越重要，关系到电力企业的生存与发展，为此，研究电力安全风险评估就变得很有必要。对整个电力系统及其结构、设备、管理和技术等进行评估监管，并制定相应防范对策，对提高和保障整个电网的安全可靠运行来讲，具有十分重要的意义［1-3］。

本文提出了一种基于模糊层次分析的综合评判方法，针对传统风险评估中存在的很多不确定因素，比如专家意见存在偏差，难以进行明确分析，但这些不确定因素却是正常、不可避免的。文中引入模糊层次分析法，克服了传统层次分析法的局限性，并结合实例，对各风险因素重要性排序，得到了更加合理的决策结果。

1 建立层次分析结构

目前电力安全生产已经成为一个世界性问题，随着经济的发展，电力系统造成的影响越来越大，由电网造成的经济等方面的事件在国内外也经常发生。人们常指的电力安全生产，即不发生人身伤亡事故、主要设备损坏事故;不发生火灾和系统大面积停电事故。我国西电东送和全国联网的战略实施，电力安全问题随着电力网络规模的日益扩大已经上升为国家安全问题［4-5］。在20世纪90年代后期，国外电力组织就制订了电力系统可靠性及风险评估相关标准或规范。2004年我国颁布了DL/T 861-2004《电力可靠性基本名词术语》，但现有的确定性评估准则及可靠性概率评估体系存在诸多缺陷［6］。因此，电力行业目前急待解决的问题是，如何将电力系统的安全风险评估体系及框架提升到政府监管下全行业实用化的阶段。根据文献［6］提出的研究成果，在应对灾变的电力安全风险评估中，采用政府与企业合作的方式，构成整个电力系统的安全风险评估体系，国内外电力系统风险事故可以划分为“因稳定破坏引起的大面积停电事故”、“因外力破坏造成电网支解的大面积停电事故”以及“针对电力系统的恐怖袭击”三种类型。对此三种类型的大面积停电事故进行分析，选取了结构、设备、管理、技术四个方面利用模糊层次分析法进行评估。

美国运筹学家T.L.Saaty教授于20世纪70年代提出了层次分析法的概念。层次分析法(AHP)的主要特点是以人脑决策思维规律为基础，结合了数学分析的方法，从决策者的选择和判断出发，通过简单的数学运算来实现目标决策。但它也存在着不可避免的缺点:判断矩阵的一致性调整需要大量的修改和计算，这可能与人们的决策思维不能保持一致，调整一致性需要调整的元素事先并不知道，通常只能根据经验调整，带有盲目性［7-9］。而模糊层次分析法可以有效解决这方面的问题，所谓模糊，主要是指客观事物间的差异在中介过程状态所呈现的亦此亦彼性，如好与坏、高与低之间都找不到明显的界限。它是一种定性和定量分析相结合的系统分析方法，由层次分析结构模型和专家判断信息，构造各层次元素的模糊判断矩阵，把复杂的决策问题用简单的两两比较形式给出［10-12］。结合模糊层次分析法的特点，建立了电力安全风险因素层次分析结构，如图1所示。

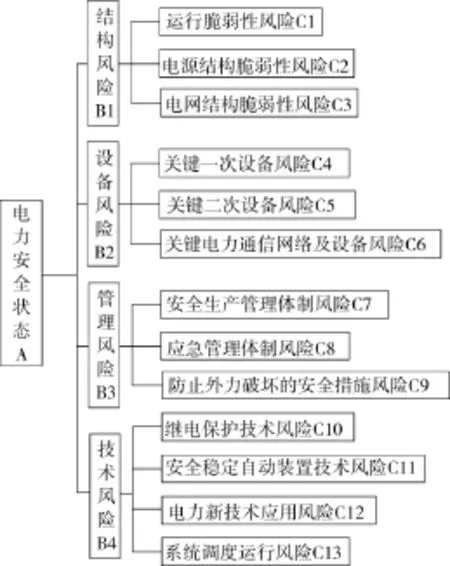
图1 电力安全风险因素层次分析结构

从图1可以看出，目标层是解决问题的目标，即设定的目标就是电力状态安全与否;准则层是实现目标所要满足的要求和条件，即从结构、设备、技术、管理风险发生时，可能给电力安全带来损失方面的风险因素进行排序;因素层是实现目标的具体方案，即电力安全中一般存在较多风险因素。

2 基于模糊一致矩阵的权重确定

在建立好层次结构模型之后，就确定了上下层次之间的隶属关系，接着就可以由该结构和专家意见构造各个层次的元素模糊判断矩阵。模糊层次分析法针对系统的不确定因素影响、1/9～9标度差异过大等问题，引入模糊一致矩阵的概念，对层次分析法进行改进，形成基于模糊一致矩阵的模糊层次分析法。

定义 1:设矩阵 R=(rij)n×n，若满足0≤rij≤1，(i，j=1，2，…，n)，则称 R 是模糊矩阵。

定义2:设模糊矩阵R=(rij)n×n，若满足rij+rji=1，(i，j=1，2，…，n)，则称模糊矩阵 R 是模糊互补矩阵。

定义3:设模糊矩阵R=(rij)n×n，若满足任意i，j，k ，有 rij=rik-rjk+0.5 ，则称模糊矩阵 R 是模糊一致矩阵。

由模糊一致矩阵计算风险因素权重的解，步骤如下，流程图见图2。

1)建立模糊互补矩阵R=(aij)n×n

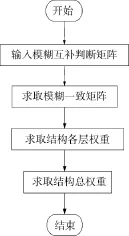
图2 风险因素权重解的流程

通过元素间的两两比较，构造模糊互补判断矩阵R=(aij)n×n，表示针对上层某准则，本层与之有关元素之间的相对重要性程度。其中aij表示第i个元素ui与第j个元素uj的相对重要性程度，其中:①aij=0.5，表示ui与uj同样重要;②aij＜ 0.5，表示uj比 ui重要，且 aij越小，uj比 ui越重要;③ aij＞ 0.5，表示ui比uj重要，且aij越大，ui比uj越重要。对于模糊判断矩阵中两两元素重要性比较的定量描述有0.1～0.9九标度定义，如表1所示。

2)求取模糊一致矩阵

根据定义3检验建立的模糊互补矩阵是否具有一致性，如果不具有一致性，则按下列方式求取模糊一致矩阵:

首先对模糊互补矩阵按行求和，记为ri=，并做如下数学变换 rij=，则由此建立的矩阵R=(aij)n×n是模糊一致的。

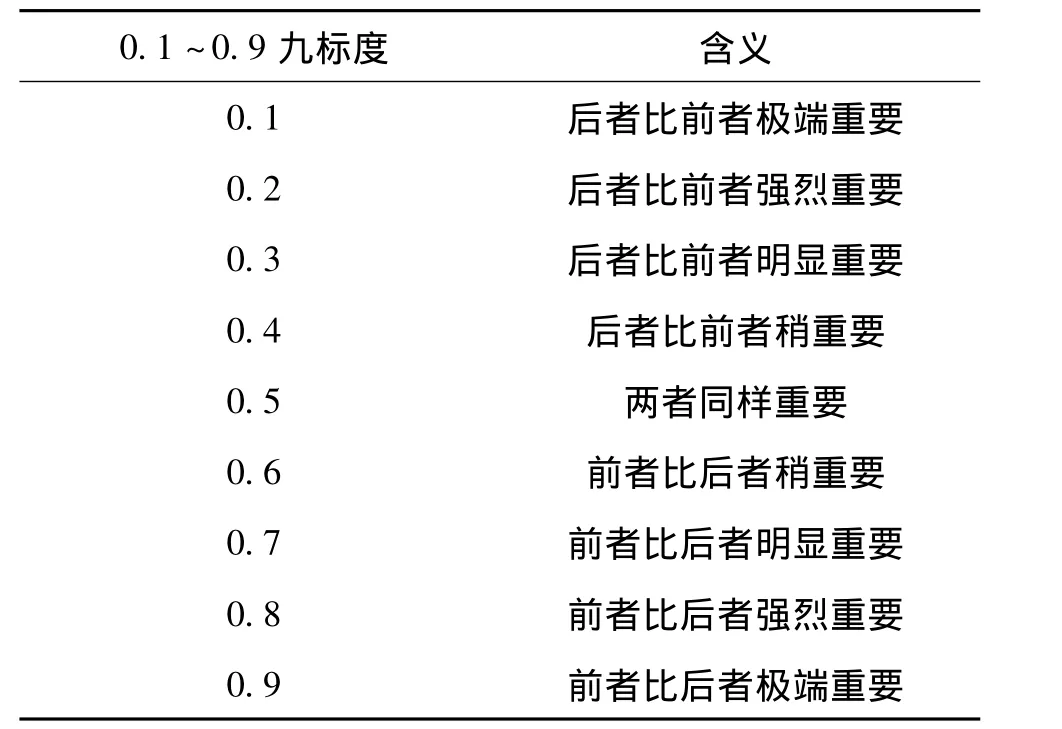
表1 模糊判断矩阵标度含义

3)求取结构各层权重

根据步骤2)采用的方法，建立由专家参与评估的模糊一致矩阵为

由模糊一致矩阵(1)采用行和归一化求得权重向量为w=(w1，w2，…，wn)T。其中权重向量满足

wi=，具体证明见参考文献［13］。

4)求取结构总权重

由步骤3)得到本层次有关元素与上一层某元素之间的相对权重，通过由目标层次到最低层次逐层进行计算，同一层次所有元素相对于目标层相对重要性的权重来比较该层所有元素相对于目标层的重要性。假设顶层A的下层B有m个风险因素b1，b2，…bm，对 A 的排序权重分别为 wb1，wb2，…wbm;而B的下一层次C有n个风险因素c1，c2，…cn，利用步骤3)求取层次C所有风险因素，对风险因素Bj的层次排序权重分别为 wc1，wc2，…wcn;当 Ci与 Bj没有联系时wcij为0;C层对A层得总权重向量WjT，可由式(2)求得:

式中，j=1，2，…，n。重复上述过程至最底层，便可以得到所有风险因素相对于目标层A电力安全状态的排序权重，实现所有风险因素的重要性排序。

3 算列及其分析

对于目标层(电力安全状态A)，假设专家根据表1对准则层的4种风险因素(结构风险B1、设备风险B2、管理风险B3、技术风险B4)两两之间对比打分，再根据第2节中步骤1)介绍方法，可获得模糊互补矩阵A:

同理，可计算出模糊互补矩阵 B1、B2、B3、B4如下所示:

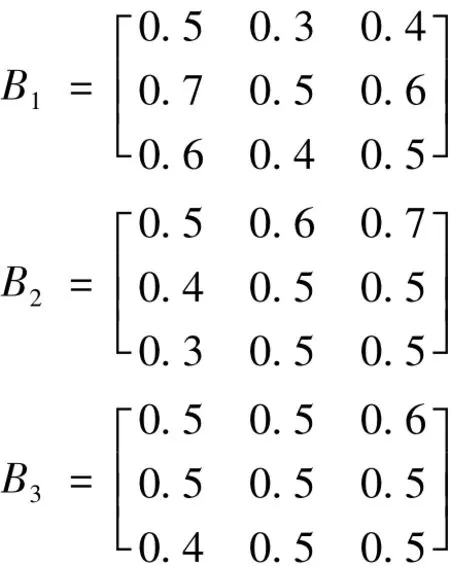
再根据第2 节中步骤2)分别求取A、B1、B2、B3、B4的模糊一致矩阵 A'、B'1、B'2、B'3、B'4，结果如下:

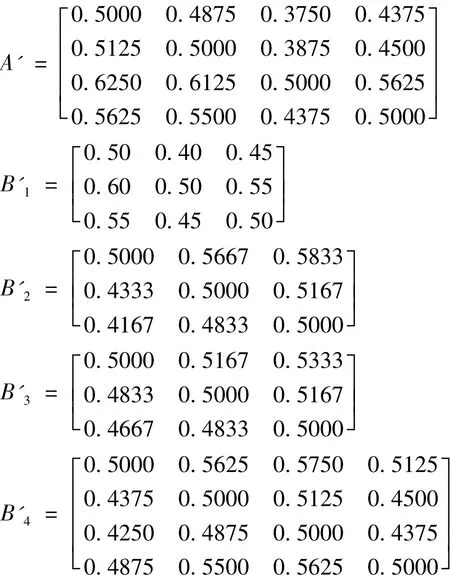
因此，根据第2节中步骤3)可分别求得权重向量

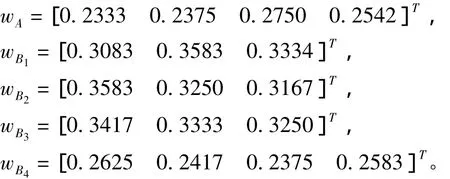
根据式(2)可以求得C层相对于A层得总权重向量

经过上述综合计算，可以得出该电力风险评估中，风险因素影响从高到低依次为:安全生产管理体制风险、应急管理体制风险、防止外力破坏的安全措施风险、关键一次设备风险、电源结构脆弱性风险、电网结构脆弱性风险、关键二次设备风险、关键电力通信网络及设备风险、运行脆弱性风险、继电保护技术风险、系统调度运行风险、安全稳定自动装置技术风险、电力新技术应用风险。

在确定以上各评价因素的基础上，还可以根据本文求得的电力安全风险因素总权重向量WjT与对应风险因素评分值的乘积，对电力系统健康状态评估，其电力系统健康程度综合总分求取公式为

式中:WjT分别为第C层对A层的风险因素的权重;j为第C层风险因素序号;Sj为第C层风险因素的评分。电力系统健康程度等级表如表2所示。

表2 健康程度等级表

可见，权重的确定极为重要，采用模糊层次分析法求取是合理可行的。

4 结论

应用模糊层次分析法确定电力安全风险因素的权重，克服了传统层次分析法应用时存在的诸多不足，并对风险因素影响重要性排序的确定更加全面和合理。由实例验证分析可知，该风险因素评估方法可以对电力系统安全风险因素进行评估，同时还可以结合后期各风险因素评分值得出系统健康状态等级，确定风险因素的优先级和采取适当管理行为，对如何采取防范风险的控制措施有重要的指导意义。

［1］高波中.电力系统常见的安全问题及其维护策略［J］.中国高新技术企业.2007，(15):84，92.

［2］张健翔.中国电网行业风险分散方式选择［J］.中国保险，2010，(9):28-33.

［3］梁中.电力工程建设项目建设期成本控制措施研究［J］.商品与质量.2011，(3):65.

［4］刘景霞，叶春青.电力安全的重要性［J］.阴山学刊(自然科学版).2006，(1):105-107.

［5］陈连栋，吕春梅.基于模糊综合评判的电力风险评估方法的研究［J］.电力科学与工程，2010，(11):50-54.

［6］侯慧，张勇传，周建中，等.应对灾变的电力安全风险评估框架及其应用［J］.电力建设，2010，(3):1-7.

［7］唐林.一种解决复杂系统决策的方法——层次分析法［J］.广西大学梧州分校学报，1997，(1):60-62.

［8］赵云飞，陈金富，郭文利.层次分析法在电力行业决策问题中的应用［J］.继电器，2005，(3):83-88.

［9］张虹.基干层次分析法(AHP)的电力信息系统安全评价［J］.陕西电力.2011，(7):76-78.

［10］吴丹，程浩忠，奚珣，等.基于模糊层次分析法的电力负荷组合预测［J］.华东电力，2006，(4):10-13.

［11］吴丹，程浩忠，奚珣，等.基于模糊层次分析法的年最大电力负荷预测［J］.电力系统及其自动化学报，2007，(1):55-58.

［12］戴喆，刘川.模糊层次分析法在电力通信中的应用［J］.价值工程，2011，(21):26-27.