多类扰动下系统综合性能的评价

李庆芝，孟庆伟

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引言

在电力生产领域中，有关过程性能评价问题的研究受到了广泛关注。很多学者在这个基础上做了大量的研究工作，提出了很多有意义的控制性能评价方法，并且有一部分评价方法在电力等领域得到了成功的应用。1989年Harris[1]提出了用最小方差控制来评价单回路控制系统的性能。B.Huang[2]等研究了在系统延迟已知的情况下设定值跟踪系统的性能评价问题，并成功地解决了在仅有某一类扰动存在情况下的系统性能评价问题，并将不同扰动下的性能评价指标统一到H2指标[3]下。然而随着发电机组容量和参数的提高，电力生产过程的复杂性显著增强，能否对机组实施有效控制不仅关系到机组的安全、稳定运行，还关系到节能、减排等综合效益。因此，如何对控制系统性能进行分析、诊断及评价，如何综合地评价电厂控制系统的控制性能，将会对现代电力工业的发展起到积极的促进作用。

控制系统性能评价主要是评估控制系统对扰动的反应控制能力，扰动问题是性能评价的主要问题。通常热工控制系统的扰动问题分为设定值跟踪问题和随机扰动问题[3～5]。设定值跟踪问题与随机扰动问题的不同主要体现在:设定值扰动为一确定性扰动而非随机性扰动。

在电力生产过程中，存在大量的不确定干扰，且大范围变负荷、机组启停等情况下机组的动态特性也会发生较大变化，在电力生产过程中设定值扰动与随机性扰动往往同时存在，而应用最小方差方法的前提是系统的设定值不变、扰动为随机性扰动，所以研究一种综合的性能评价方法势在必然[6]。

本文研究了在随机扰动存在的情况下，从已知设定值跟踪数据中重构误差信号的随机性分量和确定性分量，并将其用于计算随机性性能指标和确定性性能指标的方法，给出了该方法的一般步骤，并通过仿真及对某1 000 MW火电机组主汽压控制系统的实际运行数据进行评价，验证了该方法的有效性。

1 多类扰动下系统综合性能的评价

1.1 基本控制结构

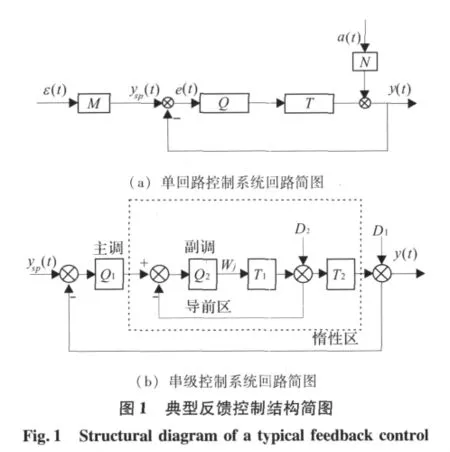
图1(a)所示的模型在电厂中是最典型的控制回路，是具有普遍意义的。

对热工控制系统进行性能评价研究，选取合适的回路模型是必要的。在确定性扰动和随机性扰动同时作用下，控制系统的一般性结构如图1(a)所示。该回路结构包含了实际热工控制系统各主要环节。对于纯单回路的系统，如给水的单冲量控制、单级三冲量控制、炉膛负压控制等等，都可以由此模型来描述;对于电厂中的串级系统如串级三冲量控制，过 (再)热器的减温水控制等，将其内回路和主对象如图1(b)虚线框中部分所示，等效看成图1(a)中的对象T，则对于串级控制的整体评价也适用于此模型;对于串级内回路是一包含主要扰动的、跟踪主控制器输出的回路，图1(b)正是其最典型的描述。

Astrom(1970)，Harris(1959)，stanfelj(1993)等人先后提出用最小方差控制作为基准指标来评价控制系统的性能指标，开创了控制系统性能评价先河，控制输出误差能很好地反映系统的控制系统的随机性能、确定性能。

由图1(a)容易得到设定值:

在该设定值下系统输出表达式:

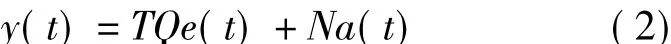
设定值跟踪误差:

将式(1)、(2)代入式(3)可得误差表达式如下:

由上式可以看出，误差是由随机性扰动影响和确定性扰动影响两部分构成。从误差e(t)中分离出确定性分量ed和随机性分量es是对系统综合评价的基础。

1.2 评价方法

1.2.1 随机扰动下的性能评价

当系统仅有随机性扰动时，很多学者作了大量的研究，尤其是最小方差指标的性能评价。

当系统的设定值为0，即ysp(t)=0，当a(t)≠0，ε(t)=0时的性能评价如下:

此时，由图1可得:

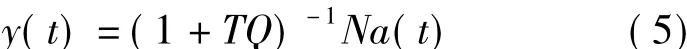
因此，随机性扰动到控制误差的传递函数为

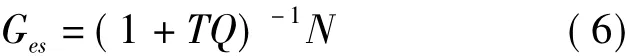
当a(t)为随机扰动时，对其进行性能评价，定义如下的H2范数:

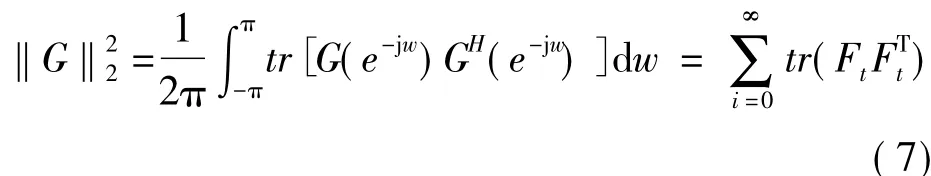
式中:Ft为G的冲击相应系数。随机性扰动到控制误差的传递函数写成多项式的形式:

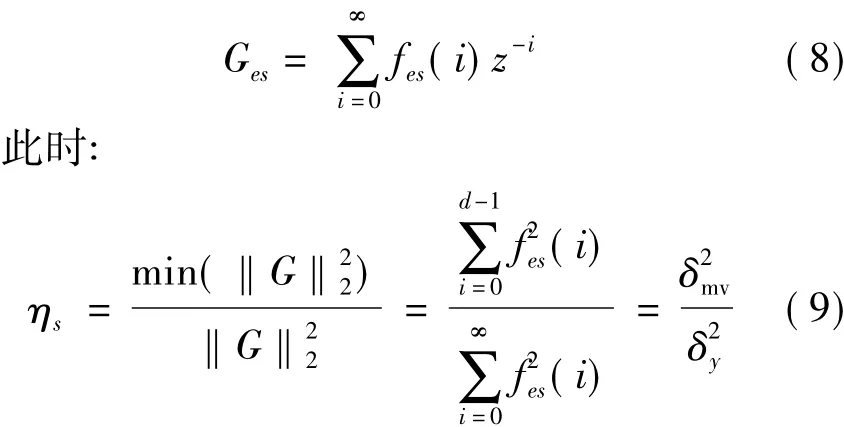
式中:d为系统延迟。ηs越接近于1，认为系统的性能越好。从上式有很多的计算方式同时可以有其他的方法来计算这一随机的性能指标，可以通过FCOR算法或者ARIMA建模来计算这一性能指标。

1.2.2 设定值变化下的性能评价

当系统仅有设定值扰动时，即a(t)=0，在此时由 (4)式易得:

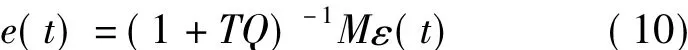
从上式可以看出，其结构与随机性扰动到误差的结构非常类似，可以采用相同的方式进行处理。此时，当αt为确定性扰动时对其进行性能评价定义如下的H2范数:

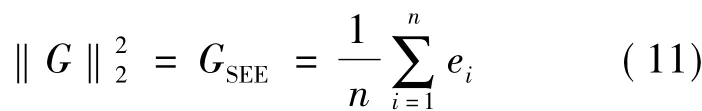
可以把单位阶跃扰动看成一冲击序列{ε(t)}={1，0，0，…}，经过 M=1/(1 － q－1)的积分后得到，此时的性能指标定义如下:

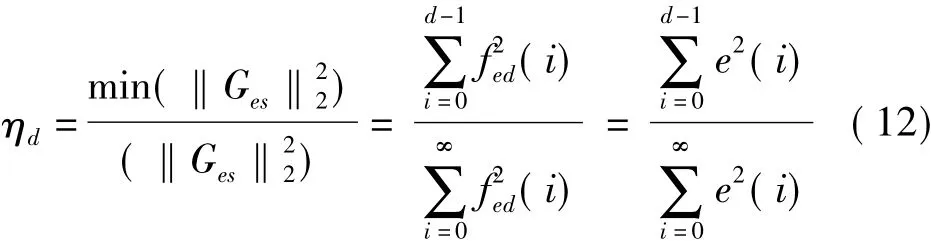
从该指标的定义容易看到，在死区过后系统越快的跟踪阶跃信号，则ηd越接近于1，系统的跟踪性能越好。

1.2.3 随机性扰动和确定性扰动同时存在下的性能评价

在设定值跟踪回路存在随机性扰动的情况下，由 (4)式可知，系统的误差不仅与随机性的扰动a(t)有关还与系统的设定值扰动有关。此时，性能指标可以通过扰动辨识和过程对象的完全辨识来计算。若通过辨识来计算相应的性能指标，则存在复杂度高、精确性差的问题。

对系统的评价应该避免采用完全辨识的办法，如1.1所述，从误差中分离出确定性分量ed和随机性分量es对系统进行综合评价不失为一种更好地选择。由此，对系统动态数据进行相应的处理来得到相应的分量分别计算系统的确定性性能和随机性性能。

对于实际的过程，假定a(t)为一零均值白噪声，系统延迟已知为d(延迟通常是通过最小二乘的方法来估计[7，8])，性能评价步骤如下:

(1)将系统输出y(t)分为两部分y1(t)和y2(t)，其中:

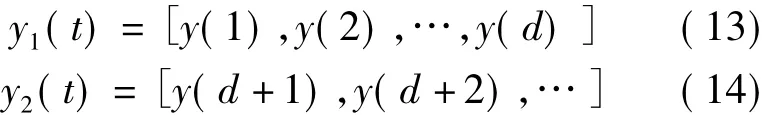
(2)对y2(t)提取其趋势项y'2(t)。用实际响应值y2(t)减去其趋势值y'2(t)得到在延迟过后时间段内随机扰动对过程的影响:

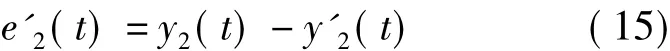
(3)误差中随机性误差分量的计算如下:

其中，y(0)为设定值的变化之前的值，上式表示在延迟内的系统响应完全是有随机扰动造成的，在延迟之后其对系统误差的影响通过步骤(2)求得。

(4)在得到es之后通过FCOR算法或者ARIMA建模计算随机误差分量的最下方差δ2esmv，由下式计算随机性能指标:

(5)误差中确定性误差分量ed计算如下:

通常就是在延迟内和在延迟之外的误差，通过设定值减去趋势值得到确定性扰动对系统误差的响应。

(6)用确定性误差分量ed代替误差e计算系统的确定性性能指标:

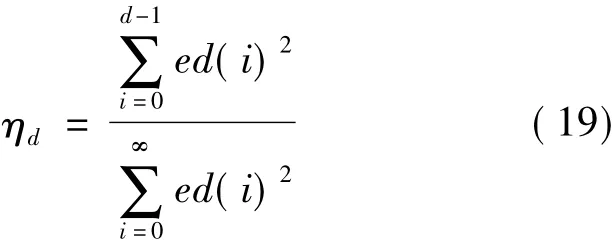
上述步骤表明，该算法计算系统的性能指标仅以系统的延迟作为先验知识，利用系统闭环操作数就可以完成。该评价算法得到的性能评价结果独立于跟踪信号和噪声信号;评价过程对系统正常运行没有任何影响，完全是非侵入性的评价;评价算法不仅适用于阶跃跟踪的性能评价，而且对于斜坡和正弦等任意类型信号的跟踪都是适用的。

2 仿真实例

本文的仿真所用模型是Eriksson和Iskasson(1994) 所用的模型[23]，该模型也被 B.Huang在研究设定值扰动时所采用。如图1所示，其中:

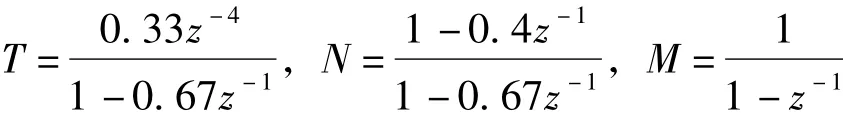
αt为一白噪声序列，=0.01，ξt为一概率密度集中在0的冲击序列，所以在ξt经过M的积分作用后产生的是确定型的阶跃扰动，延迟为4。采用 Dahlin控制器，其中 Dahlin控制器表示如下:

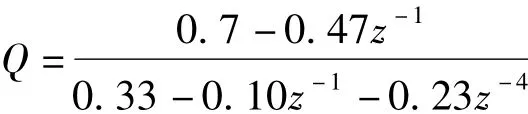
本文就设定值变化和随机性扰动同时存在时的性能评价步骤应用在该实例中。通过仿真获得系统输出，分为两段y1和y2，然后提取趋势项如图2所示。按照1.2.3中的步骤 (3)实现系统误差对随机噪声的实际响应的重构得到该随机误差分量 es，然后通过 MATLAB System Identification Toolbox建立误差到输出的传递函数，经模型定阶，模型参数估计，模型适应性检验。本文选择amx(11，10)模型来表示该随机过程，通过多项式除法得到该过程的表达式如下:

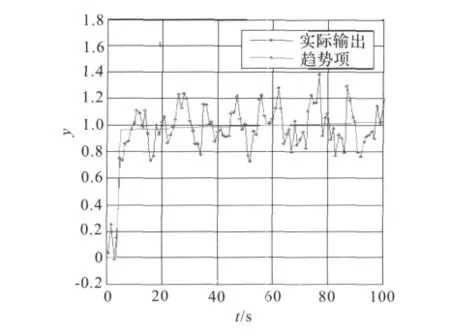
图2 系统输出曲线与其趋势线Fig.2 System output and its trend line curve

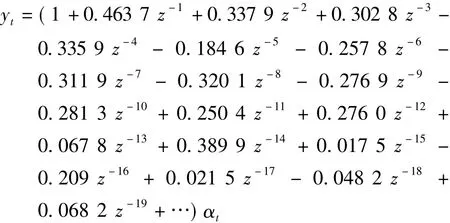
在上式中，对分量es进行ARMA建模得到随机噪声到误差的脉冲响应系数，该系数在第17项以后与之前相比明显变小，不妨取其前20由上式计算系统的随机性能指标如下:

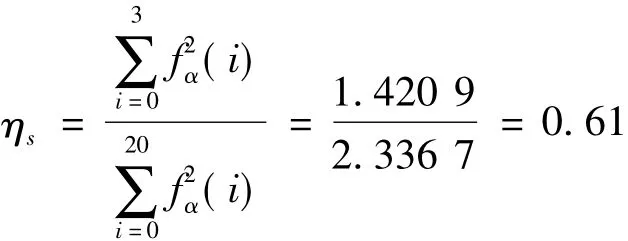
系统的设定值变化对输出误差的影响按照1.2.3中的公式 (18)重构得到，如图3中ed为误差对设定值变化相应的重构。

图3 误差曲线Fig.3 Error curve

计算系统的跟踪性能:

计算结果如表1所示，对同时存在设定值扰动和随机性扰动的系统，通过误差的分离重构后计算的随机性能指标为0.61，与理论值0.66是非常接近的，这种差距主要是噪声模型的辨识精度造成的。确定性性能指标为0.991 7与理论值0.982 4较吻合，期间的微小差别主要是由于在分母计算是有限项代替无限项的截断造成的。通过这样的对比可以发现本方法在处理含有设定值扰动和随机性扰动过程的性能评价是有效的。

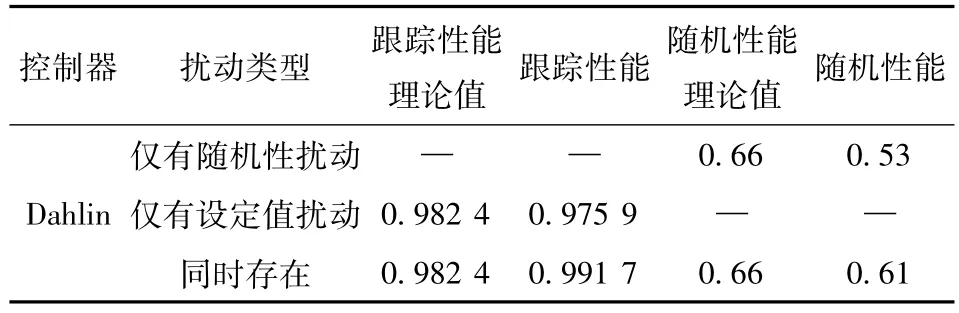
表1 不同扰动情况各性能指标的计算Tab.1 Different disturbance of each performance index calculation

3 实验研究

以某电厂1 000 MW机组的主汽压系统为例，对本文提出的方法进行分析。

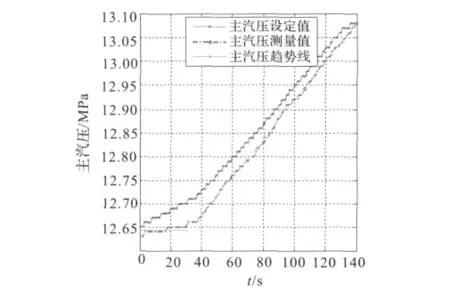
图4 主汽压及其趋势曲线Fig.4 Main steam pressure and the trend curve

图4显示的是该机组主汽压在2008年2月14日07∶43∶51 ～07∶51∶11 时间段内的跟踪状况，共计140个采样数据。已知主汽压的延迟约为30，在07∶44∶15主汽压设定值开始上升，选此时作为其初始时刻。

首先通过将数据进行分类，然后提取主汽压测量值的趋势线如图4所示，此趋势线反映的正是系统在无随机性扰动情况下的系统输出。将数据按照步骤 (3)进行处理构造出在随机扰动影响下的误差分量es如图5所示。按照相应的建模准则建立es的ARMA模型，通过计算选择amx(10，10)，然后计算得到随机噪声到误差的传递函数如下:

图5 主汽压误差曲线Fig.5 Main steam pressure error curve

采用上式中的前100项计算系统的随机性能指标如下:

首先重新构建出此时的设定值扰动对主汽压跟踪误差的影响分量ed，利用ed计算系统，此时的跟踪性能如下:

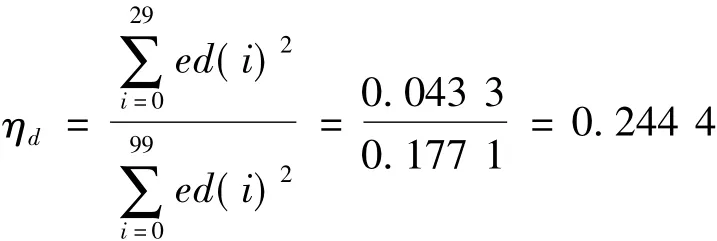
通过计算得 ηs=0.717 2，ηd=0.244 4，可以看出，该主汽压系统的抗随机性扰动的性能较好，对于当前主汽压设定值变化的跟踪性能不是很好。其跟踪性能指标值较低反映了在计算的范围内主汽压没有实现完全的跟踪，同时表征了其跟踪速度不是很快，也就是说如果能够实现完全跟踪，所需的时间相对于其延迟还是很长的。目前主汽压的跟踪静差不是很大，约为0.03 MPa，在接受的范围之内，否则控制器需要再整定以满足跟踪设定值变化的要求。

4 结论

本文提出了一种通过分离与重构误差的随机性和确定性分量，分别计算热工控制系统随机性和确定性性能指标的方法。本方法不再局限于设定值为阶跃变化这一特殊情况，对待评价系统的正常运行无任何附加影响，且实施步骤简单易行，有利于在实际中应用。

需要指出的是，与大多数控制系统性能评价方法一样，本算法也需要以系统的纯迟延作为先验知识，如何进一步改进算法或者提出新的理论来克服这一限制是进一步的研究方向;在随机噪声相对于设定值变化较大时，提取的趋势项仍然包含了很多的随机成分，不利于系统确定性性能指标的计算，但是，大多数热工控制系统中存在的随机噪声相对于设定值扰动而言并不是很大，因此，本方法的适用性可以得到保证。