偏轴传输线中的TEM波及其特性阻抗

王福谦

（长治学院 电子信息与物理系，山西 长治 046011）

0 引言

在微波工程技术的应用中，同轴线是使用十分普遍的TEM波传输线，其特点是抗干扰、无电磁辐射且频带宽。关于同轴线中TEM波的电磁场结构，在文献[1-2]中已做了讨论。但对于偏轴传输线的情形，有关刊物较少涉及。本文将利用分式线性变换分析偏轴传输线的电磁场结构，并计算出其特性阻抗。

1 TEM波的电场和磁场的分布

偏轴传输线可看作半径为R1的空心圆柱套着半径为R2的圆柱，两柱的轴线平行且相距为，其间为真空.为研究该波导横向平面上的电磁场的分布，取其中一个截面如图1所示，两圆柱的横截面为2个圆C1和C2，以圆C1的圆心为坐标原点，两圆的圆连心线为x轴建立z平面.取x轴上的a、b两点为两圆的镜像对称点，其坐标分别为x1和x2，则由对称点的定义，得：

解方程组（1）得：

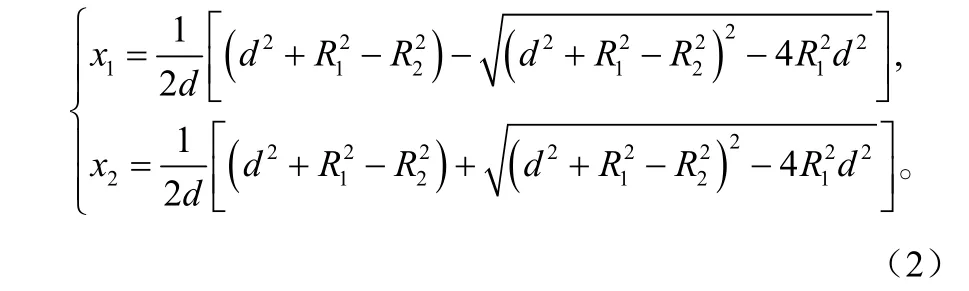
为了求出偏轴传输线横向平面内的电磁场的分布，需先把偏轴传输线变换为同轴传输线，即将圆C1和C2变换为w平面上的两同心圆。由于分式线性变换具有保圆性和对称点不变性，故作分式线性变换：

则z平面上的半径分别为R1和R2、圆心相距为d的两偏心圆C1和C2，就对应着W平面上的半径分别为R1′和R2′的两同心圆C1′和C2′，如图2所示。其中x1和x2的取值由式（2）给出。

图1 偏轴传输线的横截面

μ及ε为波导内填充介质的电磁参量，eκ为同轴传输线中TEM波的传播方向的单位矢量。

综上所述，导波装置中的TEM波的求解，可由静态场在相同边界条件下的解得到其电场和磁场在波导横截面上的分布，再乘以波动因子 e-jβκ，即得到TEM波的场解.即由静电场中所得到的ET代入式（9）得到HT的解；也可用势函数的方法求解。分别代入（3）式并取w的模，并注意到经计算得：

通过以上所作的分式线性变换，便将z平面上的半径分别为R1和R2圆心相距为d的两偏心圆C1和C2，变换为w平面上的半径分别为R1′和R2′的两同心圆C1′和C2′。即把偏轴传输线变换为同轴传输线。

图2w平面上的两同心圆

对于无限长的同轴传输线，该导波系统中的TEM横向场分量所满足的方程为[3]：

由于TEM波ET和HT在波导的横向平面上满足二维拉普拉斯方程，这与静态的电场和磁场在相同区域内所满足的方程相同，则 TEM波在波导的横截面上的分布与边界条件相同的静态场的解是相同的。但需注意的是TEM波与边界条件相同的静态场只是在规则波导的横截面上的分布一致，而它们对变量κ(κ为同轴传输线中的TEM波的传播方向)和t的关系是完全不同的：TEM 波与κ、t的关系为 ej(ωt-βκ)，即在κ向为正弦行波，且各处的场量均随时间作简谐变化，而静态场与κ、t均无关，即在k向为均匀分布，且场量不随时间变化。

TEM波的电场与磁场是由麦克斯韦方程组相互联系的，它们相互激发，不可分割，满足如下规律[3]：

对同轴传输线，其中的电场分布是径向的[4]，大小与半径成反比。即：

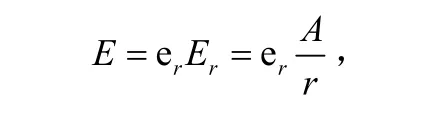
式中er为同轴传输线横截面上的径向单位矢，A为与电场幅值有关的常数。

因此，同轴线中的TEM波的电场强度为：

其中β为沿传播方向上的相位常数，对于TEM模，k=βω为工作频率）。故得电场的分布为：

式中eu、ev为同轴传输线横截面上沿横、纵轴方向的单位矢。又由式（9）、（11），得：

式(11)、(12)为同轴传输线中 TEM 波的场解。其中为介质的波阻抗，η与相同的无界媒质中的均匀平面波的波阻抗相同，对于真空，其波阻抗为

由式（3）式，有

将上式中的u、v表达式代入式（11）、（12），并建立z平面的坐标系使则有：

式（13）、式（14）为TEM波在偏轴传输线横截面上的电场与磁场的分布表达式。其中x1、x2及R1′、R2′分别由式（2）和式（5）给出。

图3为利用数学软件MATLAB所绘制出的TEM波在偏轴传输线的横截面上的径向电场线及φ向（横向）磁感线的分布图。其中R1=4m、R2=2m，d=1m，V0=100V。

由图3及式（13）、式（14）可见，在偏轴传输线内部，愈靠近内导体表面，电磁场愈强.因此内导体的表面电流密度较外导体内表面的表面电流密度大.所以偏轴线的热损耗主要发生在截面尺寸较小的内导体上。

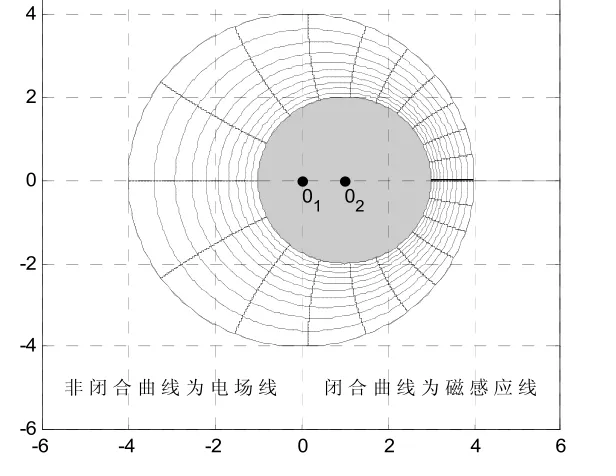
图3 偏轴线TEM模的场结构（一）

图4为过偏轴传输线的一纵截面（过图1中的x轴）径向电场线及φ向（横向）磁感线的分布图。

2 传输特性

对于上述保角变换将偏轴传输线截面变换为同心圆环形区域，由于变换前后电缆单位长度的电容保持不变，这样就可以方便地求出其特性阻抗。偏轴传输线特性阻抗z0与单位长度电容C0的关系为[5-6]：

式中ε和μ为传输线内填充介质的介电常数和磁导率。

当传输线内为真空时，有：

而由保角变换给出的偏轴传输线单位长度的电容为[7]：

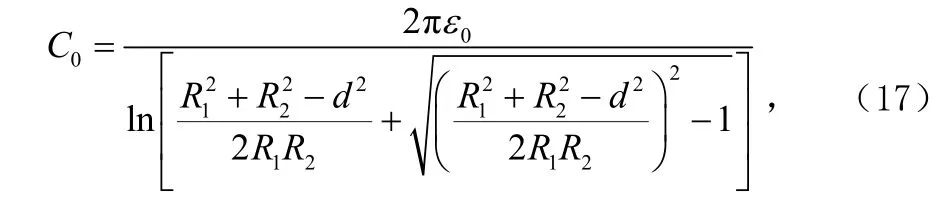
则偏轴传输线的特性阻抗为：

由保角变换法计算偏轴传输线特性阻抗的结果，可用于检验其他近视计算结果的精确度。

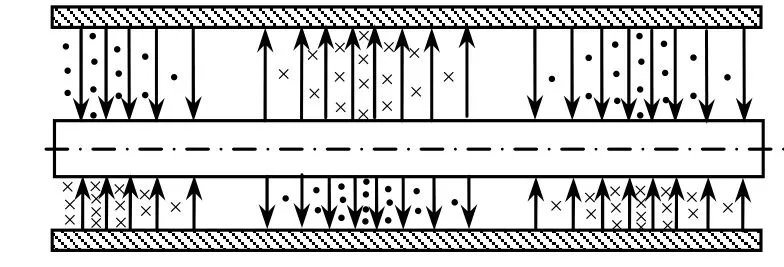
图4 偏轴线TEM模的场结构（二）

3 结语

因为 TEM波传输线是工业上最常用的传输线，传输线内 TEM波的场分布，对于了解传输线的功率容量、计算衰减常数、考虑功率耦合及设计有关的有源器件等都是不可缺少的。该文所讨论的偏轴传输线内的TEM波，属于偏心结构问题。该问题的研究不仅能解决偏心特种截面传输线的计算问题，而且可为一般同轴线的加工精度提供理论依据。因此，该文的研究结论，对于传输线的性能的分析及新型传输线的研发具有一定的理论意义和实用价值。

[1]沈熙宁.电磁场与电磁波[M].北京：科学出版社，2006: 406-409.

[2]吴万春.电磁场理论[M].北京：电子工业出版社，1985: 252-253.

[3]冯恩信.电磁场与电磁波[M].西安：西安交通大学出版社，2005:282-283.

[4]沈熙宁.电磁场与电磁波[M].北京：科学出版社，2006: 349-382.

[5]朱满座.数值保角变换及其在电磁理论中的应用. [DB/OL].(2008-12-12)[2011-05-20].http//www.cnki.net/kcms/detail/de tail/aspx.

[6]曹桂明，王积勤. 方同轴线的特性分析[J].上海航天,2003(02):27-29.

[7]梁昆淼.数学物理方法[M].北京：高等教育出版社，1998: 433-440.