地铁换乘客流实时监测模型研究
2011-08-10徐永能
丁 蕾 徐永能 姜 毅
(南京理工大学交通工程系 南京 210094)
随着我国城市轨道交通的高速发展,城市轨道交通正步入网络化时代。地铁换乘站是城市轨道交通线网中的重要节点,轨道交通不同线路间的内部换乘是换乘站的重要功能之一,其内部换乘效率的高低直接影响整个轨道交通的运能,而换乘客流信息又是影响乘客内部换乘效率的重要因素之一。
目前,在客流量较大的早晚高峰时段、节假日及有特殊活动举办的时段,换乘站客流拥堵的现象时有发生。当换乘客流不能及时得到疏散时,乘客的安全隐患将会大大增加,乘客满意度也随之降低。换乘客流的到达并非连续均衡,而是随列车的到达呈现脉冲式的分布规律。因此,在网络化运营条件下,对换乘客流进行实时的监测,有助于了解换乘站大客流的突发状况,做好应对方案,从而提高城市轨道交通客流输送能力,提高运营服务质量。
由于地铁换乘客流的影响因素复杂、形成机理模糊,在换乘客流模型构建和方法选取的过程中,需要考虑模型和算法能否应对随机因素强的系统结构。目前,轨道交通还没有针对换乘客流的短时客流预测方法,而常见的短时客流预测方法,难以应对影响因素复杂、随机性强的系统。故笔者结合神经网络识别复杂非线性系统的特性,采用BP(back propagation反向传播)神经网络算法,构建一种基于时序倒推的换乘客流实时监测模型。
1 换乘客流实时监测模型的构建
1.1 基于时序倒推的实时监测模型
地铁换乘站换乘客流的突发性并非没有规律可循,它和各站点的进、出站客流具有密不可分的联系,可以依据各站点到达换乘站的时间规律监测各站点相应时段的客流数据,并将各站点的需求数据导出,结合历史数据及其他因素数据进行预测,最终达到实时监测的目的,构建一种基于时序倒推及站点实时监测的换乘客流预测模型。

图1 网络结构
如果需要预测tk到tk+1时段Tk,k+1的换乘站(点O)的换乘客流,依据时间倒推原理,相应地需要得知站点在(到tk'+1()时段间的进站客流数据。其中

式中,t0为各站乘客进站到候车区的平均时间,ε为该站点所在线路的列车发车间隔。
1.2 监测模型的神经网络结构设计
在对地铁换乘客流进行实时预测时,换乘客流与各站点进站客流及换乘站出站客流、各站点到换乘站换乘的时间有着必然的联系,因此在站点客流预测的结构设计中,通过1.1节提到的思路,选取与换乘站待预测时段相对应时段的各站点进站客流作为输入层,选取换乘站待预测时段各方向的换乘客流作为输出层。
假设待预测的换乘站为某两条线的换乘站,现在需要预测两条线相互换乘的客流量,那么输入层选取对应时段所有可能在该换乘站换乘的各站点进站客流,神经元的个数为选取站点的个数,而输出层则采用2个神经元。
地铁换乘客流监测模型的神经网络结构如图2所示。

图2 客流监测网络结构设计
2 算例应用
2.1 南京地铁线路情况简介
南京地铁1号线全长为21.72 km,共16个站。地铁2号线是一条连接主城中心和城市副中心的东西向骨干线,全长37.545 km,共设26座站点。地铁1号线南延线全长24.47 km,全线将设15个站,其中高铁南京南站正在规划中,地铁南京南站未开通。目前,南京地铁已开通3条线路,54个站点(不含南京南站),其中新街口站为1号线主线和2号线主线的相互换乘站,元通站为1号线西延线和2号线主线的相互换乘站。
2.2 基础数据准备
训练数据的准备工作是网络设计和训练的基础,数据选择的科学合理性以及数据表示的合理性对于网络设计具有极为重要的影响。考虑到换乘客流的短时冲击性,选取15 min作为一个预测时段。输入样本的时间段选取参见1.1节中提到的思路,其中输入样本取各站点进站客流的统计数据值;输出样本的时间段对应预测的时段。以南京地铁典型换乘站新街口2010年6月30日(星期三)的换乘客流预测为例进行分析。
从最佳路径考虑,元通站的进站乘客可直接换乘,无需经过新街口站进行换乘。因此,选取除去元通站和新街口站的另外52个进站客流作为训练的输入样本,选取新街口各线路间的换乘客流为输出样本。
由于工作日和非工作日的客流特点存在较大差别,为检测工作日与非工作日的样本对预测值的影响,选取3种方案。在方案1中的网络学习样本里不考虑工作日与非工作日的区别,选取前27 d的数据为初始网络学习数据,后2 d的数据为修正网络的训练数据。在方案2中的网络学习样本里去除8个非工作日的样本数据,其中前19 d的数据为初始网络学习数据,后2 d(工作日)的数据为修正网络的训练数据。方案3选取与方案2相同的网络学习样本个数,选取2010年6月9—29日对应的各站点进站客流数据统计值和换乘客流数据统计值作为训练样本,进行模型训练对比。其中,前19 d的数据为初始网络学习数据,后2 d的数据为修正网络的训练数据。30日当天各站点对应时段的进站客流数据统计值为预测的输入样本,最后通过BP神经网络预测出当天早高峰时段(8:00—8:15)各线路间的换乘客流量,并与实际的换乘客流量进行误差分析。各方案样本信息如表1所示。

表1 客流预测样本准备
2.3 模型检验
依据上述训练步骤,对样本数据进行归一化处理,建立一个串联前向BP网络,选取带有附加动量法和自适应的梯度下降法traingdx为网络训练函数,设定权值激活函数及相应的训练参数,输入样本进行训练。各方案的训练误差性能曲线如图3所示。

图3 训练误差性能曲线
建立自适应网络函数adapt,利用样本数据自适应前面构建的BP神经网络,并对误差进行修正。最后利用已构建的BP神经网络进行网络仿真,并对网络仿真的输出预测值进行反归一化处理,得到实际的换乘客流预测值。
将预测的输出数据与真实的数据进行对比,样本的预测值与真实值对比如图4所示。
各方案的样本预测值及真实值详见表2。

图4 样本预测对比
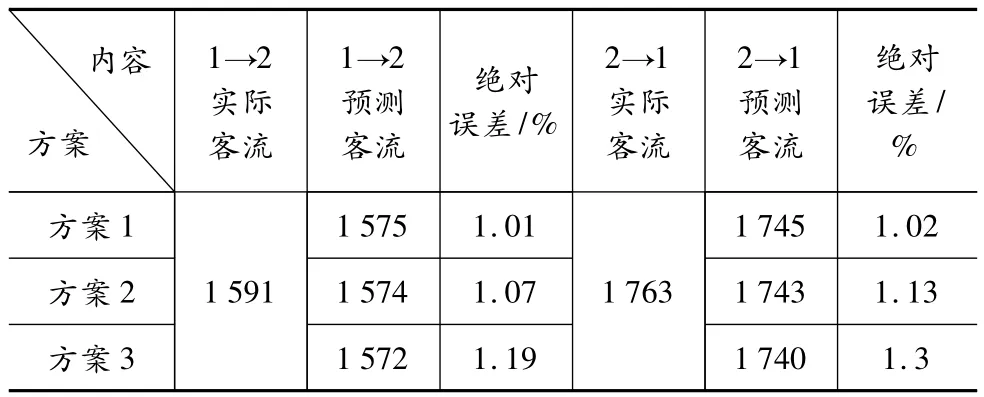
表2 样本训练结果对比 人次
由图3可知,上述3种方案训练曲线的均方误差都达到了目标值。3种方案的换乘客流预测值与实际值的误差也在误差允许范围内,且各方案的换乘客流预测值之间相差不大。当网络学习样本量较大时,预测精度相对有所提高,但样本学习中是否区分工作日与非工作日的数据,对预测结果影响不大。
3 结语
通过模型求解和算例分析,说明了基于时序倒推的地铁换乘客流实时监测模型,在随机性较强的系统中,抗干扰性较强,具有一定的可行性。随着闸机技术的升级、数据采集速度的提高及各系统的升级,可进一步考虑换乘客流预警系统的应用。
[1]王进,史其信.短时交通流预测模型综述[J].中国公共安全: 学术卷,2005,6(1):92-98.
[2]童飞.基于 BP神经网络的水上交通事故预测及MATLAB实现[D].武汉:武汉理工大学,2005.
[3]飞思科技产品研发中心.神经网络原理与MATLAB7实现[M].北京:电子工业出版社,2005:99-104.
[4]毛保华.城市轨道交通系统运营管理[M].北京:人民交通出版社,2006.
[5]王袆南.突发特大客流城市轨道交通运营组织研究[D].北京:北京交通大学,2008.
[6]杨永凯,宋瑞,李海荣.地铁客流预测模型的分析与研究[C]//第四届中国青年运筹与管理者大会论文集.北京:清华大学,2001:276-281.
[7]康海燕,郑世枚,吴倩.地铁换乘站客流组织研究[J].铁道运输与经济,2009,31(8):89-90.
[8]王波,李晓霞,安栓庄.轨道交通换乘站客流特性分析及车站设计[J].都市快轨交通,2010,23(2):55-58.
