一种相干复合高斯海杂波仿真方法＊

张社国 薛文虎 白海东

（海军工程大学研究生院1） 武汉 430033）（海军工程大学电子工程系2） 武汉 430033）

（武汉军械士官学校3） 武汉 430075）

1 引言

严重杂波环境中的目标检测是现代雷达面临最大挑战性问题之一。对雷达而言，当工作于低掠射角、高海况条件[1～2]时，这种环境就是典型的强海杂波环境。强海杂波下目标的准确检测需要知道背景海杂波的统计特性。建立一个能够准确描述海杂波幅度分布特性和空间相关特性的模型对最优检测算法设计和雷达性能评估具有十分重要的意义[3]。

国内外对海杂波进行了大量的实验研究，早期对于低分辨率雷达，一般假设杂波回波为独立同分布的高斯分布。然而，当雷达分辨率足够高时，海杂波具有了严重的“拖尾效应”及非对称性等非高斯特征。因此，具有拖尾的复合高斯模型[4]已受到广泛的关注和支持，从理论和经验上描述了雷达信号处理中杂波回波的统计特性。

本文介绍了海杂波复合高斯模型，并采用无记忆非线性变换（MNLT）的方法产生海杂波序列，并对结果进行了分析。

2 复合高斯海杂波模型

在该模型中，来自海面的反射海杂波被认为是由于两种成分构成的，这两种成分与不同的现象相对应。一种是小尺度结构，以短的相关时间和空间独立为特征，被称为散斑（speckle）。散斑是一种快速起伏成分，用于解释局部散射，它符合复高斯分布，主要是受贴近海表面的风影响形成的较小的毛细波浪影响，波长一般为厘米级。另一种为大尺度结构，或纹理（texture），是一种调制散斑的慢速起伏成分。纹理反映了杂波的局部平均功率，且依赖于海况、风、涌，表现出空间和时间的相关性。它已被建模为多种分布，如伽马分布、逆伽马分布、威布尔分布、对数正态分布等。

根据复合高斯模型，第i个杂波散射源的反射系数[5]为

其中散斑Si为平稳复高斯过程，其中均值为零，协方差为Σ。纹理Ti≥0，为一非负随机过程。因此，给定Ti和Σ，yn～CN（0，TnΣ）。利用 McMaster大学IPIX雷达采集了奥斯本靶场的经验海杂波数据，对这些数据进行分析发现，散斑在1～5ms时间内相关，而纹理在50～60s内保持相关[6]。

3 复合高斯海杂波产生方法

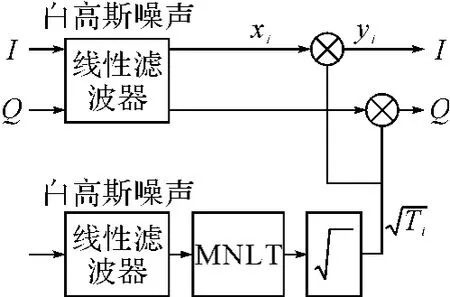
图1 复合高斯海杂波产生框图

假定海杂波散射源均匀分布在距离单元内，复合高斯模型海杂波产生过程如图1所示。图1中上部分为散斑的同相分量（I）和正交分量（Q）的产生，是由白高斯噪声经线性滤波器后，产生了时间相关，具有特定的协方差Σ的复散斑分量。下部分为由白高斯过程经MNLT后产生的Gamma序列，即纹理分量，为非负值。

3.1 纹理分量的产生

在很多情形下，正是慢变化的纹理分量影响雷达的性能。因此，海杂波仿真实现的一个最重要的问题，就是如何快速准确地产生具有任意相关性的Gamma过程，即纹理分量。下面先介绍产生Gamma随机过程序列的MNLT方法。

3.1.1 MNLT方法

设一零均值，单位方差的高斯随机变量x，其概率密度函数为

其相关函数定义为

其中RG（t）为高斯过程的相关系数。则x（0）、x（t）的联合概率密度为

高斯随机过程经线性变换后，仍为高斯随机过程，但可给定其均值与方差，且相关系数可由某一特定的滤波器所产生[7]。

Gamma随机变量y，概率密度为

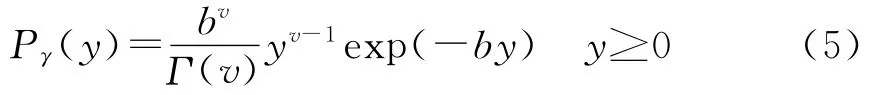
b和v分别为尺度参数和形状参数。与高斯过程相似，其相关函数为

Gamma分布的随机过程经线性变换后不是Gamma分布的随机过程，这是由其分布的无限可分特性决定的，与高斯随机过程稳定性所不同[8]。因此，产生具有特定相关函数的Gamma随机过程没有高斯过程容易。

一个改进的方法就是，通过相关的具有零均值和单位方差的高斯随机过程经无记忆非线性变换（MNLT）产生相关Gamma过程。其方法是解如下方程：

MNLT建立了一个高斯过程与Gamma过程累积分布函数之间的关系，即

对于给定相关特性的高斯时间序列可以通过该方法产生具有某种特定相关函数的Gamma序列。由于该方法的非线性，要获得精确海杂波模型就必须建立相关高斯分布随机序列与Gamma随机序列的相关函数间的关系[9]。

3.1.2 经MNLT后的相关函数

高斯过程经MNLT后产生Gamma过程的相关函数可通过下式计算

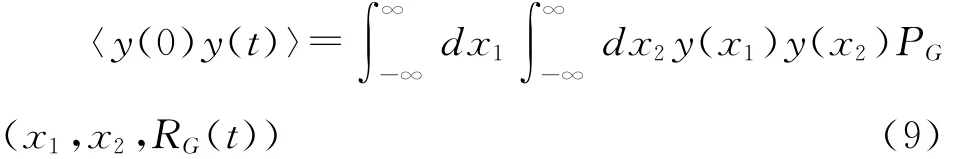
上式中二维积分运算可经下式代替

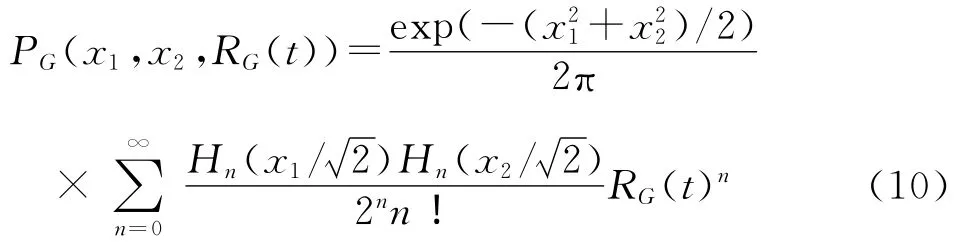
其中Hn为Hermite多项式，定义为

该联合概率密度函数的表达式为输入相关函数的一幂级数序列，易于输出相关函数的计算，也可以通过前者改进输出相关函数[9]。将式（10）代入式（9），可得输入与输出相关函数关系为

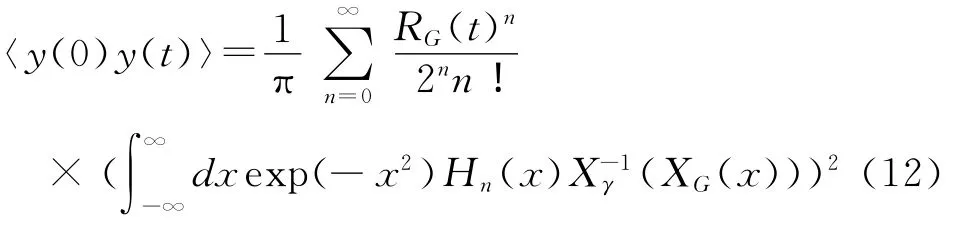
输入高斯过程与输出Gamma过程相关函数之间关系的幂级数序列表达式，且一般仅取前几项进行计算，可以看到该序列是快速收敛的或可解析求和[10]。图2为两序列间的相关函数间关系。

3.1.3 Gamma序列的产生

给定Gamma序列的参数值如b＝1，v＝0.7，及相关函数，通过式（12）获得高斯序列的相关函数，再产生高斯序列，后经式（8）得到想要的Gamma序列。图3就是利用上述方法产生的1000点Gamma序列，即纹理分量。

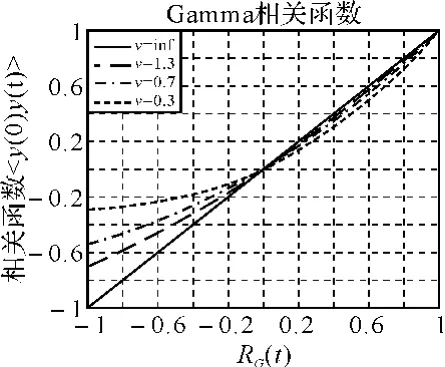
图2 Gamma序列与高斯序列相关函数间关系

图3 相关Gamma序列

3.2 散斑分量的产生

从图1可以看出，散斑分量的产生主要是将输入的高斯随机序列转换为一个具有特定协方差的高斯序列。而高斯过程通过一个线性系统后仍然是高斯过程，设输入高斯序列为X＝[X1，X2，…，Xn]，输出相关高斯序列为Y＝[Y1，Y2，…，Yn]，则

L为线性变换矩阵，Y的概率密度函数为

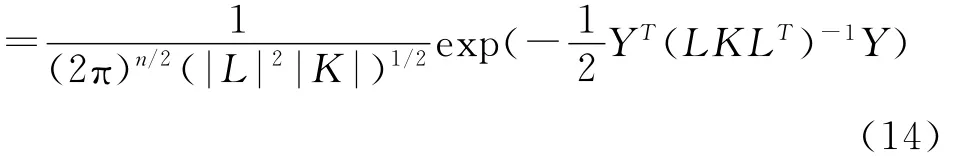
式中J为雅克比行列式，K为X协方差，令

所以，散斑分量产生比较容易，首先给定其输出高斯序列的协方差阵F，对其进行Schur分解即可得到线性变换矩阵L，再将其代入式（13）中即可获得所需序列。图4即为采用上述方法产生的1000点的散斑分量。

4 仿真结果及分析

利用第三节所述原理产生的纹理分量与散斑分量的基础上，按照图1，即根据海杂波复合高斯模型定义即可仿真海杂波序列，如图5所示，其中形状参数为v＝0.7，海杂波序列为1000点数据。

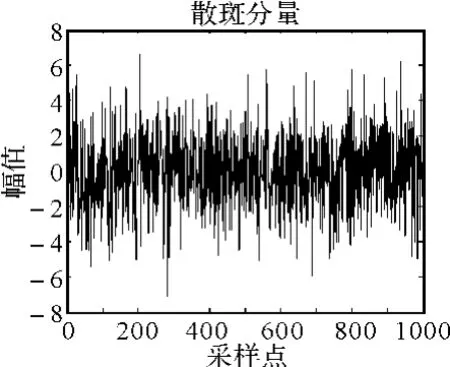
图4 散斑分量序列

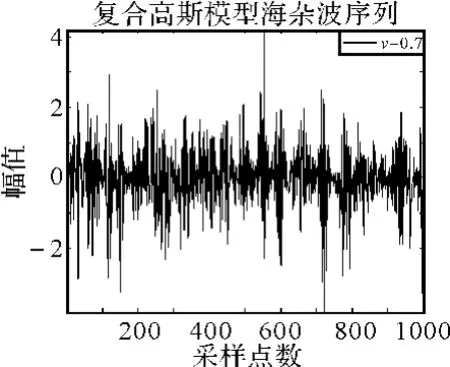
图5 仿真海杂波序列

该文采用Mcmaster大学IPIX雷达在加拿大东海岸Dartimouth湾测得实际海杂波数据，与仿真的复合高斯海杂波进行对比分析[11]。以实际海杂波数据库中＃269文件中“Hi.zip”为例，其中数据已被预处理为ascii格式，包含3个距离单元，采用VV极化方式。

对实际海杂波与仿真海杂波进行幅值对比分析发现，具有较高的相似性，且其概率密分布相差不大，具有较好的匹配性，如图6所示。同时它们功率谱对比分析，也表现出较好的类似性，见图7。

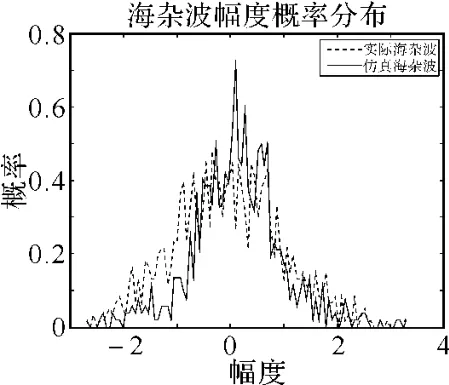
图6 幅度对比分析

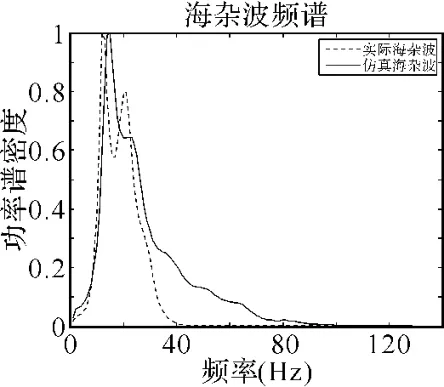
图7 功率谱对比分析

5 结语

该文分析了海杂波的复合高斯模型，详述了MNLT产生海杂波的方法，通过仿真产生了复合高斯模型的海杂波。与实测数据进行对比分析，在幅度分布与功率谱密度与高海况条件下，高分辨率雷达的实际海杂波匹配度非常高，表明了MNLT方法的有效性。复合高斯模型海杂波可以准确描述高分辨率海杂波统计特性，可用于雷达最优检测算法设计及雷达系统性能评估，具有十分重要的意义。

[1]Y.Li，S.P.Sira，A.Papandreou－Suppappola，et al.Maximzing Detection Performance with Waveform Design for Sensing in Heavy Sea Clutter[C]／／IEEE Statistical Signal Processing Workshop，Madison，WI，2007，8：249～253

[2]S.Suvorova，B.Moran，M.Viola.Adaptive modeling of sea clutter and detection of small targets in heavy sea clutter[C]／／IEEE International Radar Conference，2003：614～618

[3]谢洪森，邹鲲，周鹏.低掠射角海杂波的统计特性分析[J].雷达科学与技术，2011，9（2）：172～179

[4]S.P.Sira，D.Cochran，A.Papandreou－Suppapppola.Adaptive waveform design for improved detection of low－RCS targets in heavy sea clutter[J].IEEE Journal on Special Topics in signal Proceeding，2007（1）：56～66

[5]J.Wang，A.Dogandzic，A.Nehorai.Maximum likelihood estimation of compound－Gaussian clutter and target parameters[J].IEEE Transactions on Signal Processing，2006，54（10）：3884～3898

[6]S.Haykin，R.Bakker，B.W.Currie.Uncovering nonlinear dynamics－The case study of sea clutter[J].Proc.IEEE，2002，90（5）：860～881

[7]罗鹏飞.统计信号处理[M].北京：电子工业出版社，2009：15～18

[8]Ward K D，Tough R J A，Shepherd P W.Modelling sea clutter：correlation，resolution and non－Gaussian statistics[C／／Proc.Radar 97，IEE pub，1997：386～397

[9]Tough R J A，Ward K.D.The correlation properties of gamma and other non－Gaussian processes generated by memoryless nonlinear transformation[J].Phys.D，1999，32：3075～3084

[10]G.Davidson.Simulation of coherent sea clutter[J].IET Radar，Sonar and Navigation，2010（4）：168～177

[11]Simon Hakin[EB／OL].http：／／soma.mcmaster.ca