基于罚函数的小生境遗传算法在MATLAB中的实现
2011-08-08蒋昀昕
蒋昀昕
(福建卫生职业技术学院公共基础部,福建 福州 350101)
1.引言
生物学上,小生境(niche)是指在特定环境中一种组织(organism)的功能,把有共同特性的组织称作物种(species)。小生境技术就是将每一代个体划分为若干类,每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群,再在种群中以及不同种群中之间杂交、变异产生新一代个体群。同时采用预选择机制和排挤机制或分享机制完成任务。基于这种小生境的遗传算法 (Niching Genetic Algorithms,NGAs),可以更好地保持解的多样性,同时具有很高的全局寻优能力和收敛速度,特别适合于复杂多峰函数的优化问题。常见的小生境遗传算法主要有适应值共享遗传算法、拥挤遗传算法、隔离小生境遗传算法等。在小生境遗传算法中,为了使个体能够在整个约束空间分散开来,更好地维护种群的多样性,有学者提出在传统的小生境遗传算法中引入罚函数的思想。本文从编程角度出发,详细阐述如何使用MATLAB语言实现该算法并给出数值实验测试。
2.罚函数法
实际应用中的优化问题一般都含有一定的约束条件,它们的描述形式多种多样[1]。在构造遗传算法时,罚函数法是处理约束条件的常用方法之一。
这种处理方法的基本思想是:对在解空间中无对应可行解的个体,计算其适应度时,处以一个罚函数,从而降低该个体的适应度,使该个体被遗传到下一代群体中的机会减少。即用下式来对个体的适应度进行调整:

式中,F(X)为原适应度,f(x)为考虑了罚函数后的新适应度,G(X)为罚函数。
在确定合理的罚函数时既要考虑到度量解对约束条件不满足的程度,又要考虑遗传算法在计算效率上的要求。如果罚函数的强度太小,部分个体仍有可能破坏约束条件,所以保证不了遗传运算所得到的个体一定是满足约束条件的一个可行解;反之,如果罚函数的强度太大,又有可能使个体的适应度差异不大,降低了个体之间的竞争力,从而影响遗传算法的运行效率。
3.基于罚函数的小生境遗传算法思想
在小生境遗传算法中引入罚函数的目的是为了使个体能够在整个约束空间分散开来,更好地维护种群的多样性。该算法的思想是:首先两两比较群体中各个个体之间的距离,若这个距离在预先指定的距离L之内的话,再比较两者之间的适应度大小,并对其中适应度较低的个体施加一个较强的罚函数,极大地降低其适应度。这样,对于在预先指定的某一个距离L之内的两个个体,其中较差的个体经处理后其适应度变得更差,它在后面的进化过程中被淘汰掉的概率就极大。也就是说,在距离L之内将只存在一个优良的个体,从而维护了群体的多样性,又使得各个个体之间保持一定的距离,并使得个体能够在整个约束空间分散开来。算法的步骤可描述如下:
(1)设置进化代数计数器t=1;随即生成M个初始个体组成初始群体P(t),并求出各个个体的适应度Fi(i=1,2,…,M)。
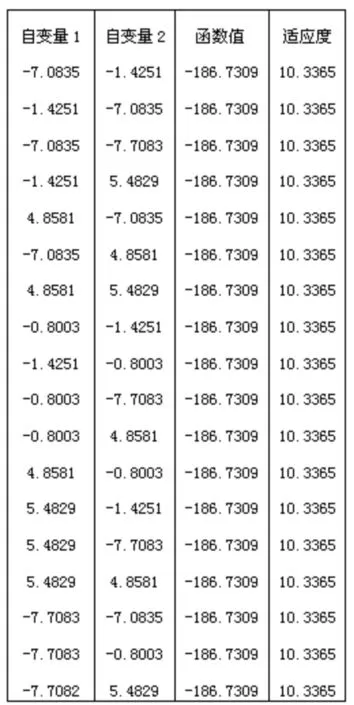
(2)依据各个个体的适应度对其进行降序排序,记忆前N个个体(N (3)选择运算。对群体P(t)进行比例选择运算,得到P1(t)。 (4)交叉运算。对选择出的个体集合P1(t)作单点交叉运算,得到 P2(t)。 (5)变异运算。对P2(t)作均匀变异运算,得到P3(t)。 (6)小生境淘汰运算。将第(5)步得到的M个个体和第(2)步所记忆的N个个体合并在一起,得到一个含有M+N个个体的新群体;对这M+N个个体,按照下式求出每两个个体Xi和Xj之间的海明距离: 当时‖Xi-Xj‖<L,比较个体个体Xi和Xj之间的适应度大小,并对其中适应度较低的个体处以罚函数: (7)依据这M+N个个体的新适应度对各个个体进行降序排序,记忆前N个个体。 (8)终止条件判断。若不满足终止条件,则更新进化代数计数器t=t+1,并将第(7)步排序中的前M个个体作为新的下一代群体P(t),然后转到第(3)步;若满足终止条件,则输出计算结果,算法结束。 MATLAB是Matwork公司的产品,是一个功能强大的数学软件,其优秀的数值计算能力使其在工业界和学术界的使用率都非常高。MATLAB还十分便于使用,它以直观、简洁并符合人们思维习惯的代码给用户提供了一个非常友好的开发环境[2]。本算法的程序是在MATLAB环境下编写完成的,具体代码如下: 本文中的编码方案采用的是最常用的二进制编码,即用二进制数构成的符号串来表示一个个体。使用randint函数实现编码并产生初始群体: 在上述代码中,PS是种群个数,GL是个体编码长度,VN是决策变量的个数。此代码的含义是随机产生一个种群大小为PS的初始化群体initpop,且每个个体的二进制编码长度为GL*VN+VN+2。 初始化的种群initpop必须通过解码才能计算函数值与适应度。代码过程如下: 选择操作建立在对个体的适应度进行评价的基础之上。选择操作的主要目的是为了避免基因缺失,提高全局收敛性和计算效率。本文中的选择算子是最常用的比例选择算子。代码过程如下: 本文采用单点交叉的方法来实现交叉算子,具体代码过程如下: 本文采用均匀变异的方法来实现变异算子,具体代码过程如下: 在小生境淘汰运算中,正确地选择罚函数是关键。具体代码过程如下: 利用MATLAB中的Sort()函数对种群进行排序,具体代码如下: 以Shubert函数为测试函数,测试参数为种群规模200,个体编码长度20,交叉概率0.9,变异概率0.01,罚函数Penalty=1.0e-030。 此函数共有760个局部极小点,其中18个为全局最小点,最小值为-186.7309。 图1给出某一次计算出的18个全局最小点的具体数值,其中第1、2列为横、纵坐标,第3列为目标函数值,第4列为适应度。这个结果的精确度不仅超过了所有公开报道的计算结果,而且比以往我们计算的结果更好。 图1 全部18个全局最小点示意图 本文介绍了基于罚函数的小生境遗传算法,给出了用MATLAB编写的完整代码,并通过MTALAB测试。数值实验结果表明随着进化代数的增加,基于罚函数的小生境遗传算法具有较好的多峰搜索能力。 [1]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999. [2]张宜华.精通MATLAB5[M].北京:清华大学出版社,1999.

4.算法实现
4.1 编码运算

4.2 解码运算

4.3 选择运算


4.4 交叉运算

4.5 变异运算

4.6 小生境淘汰运算
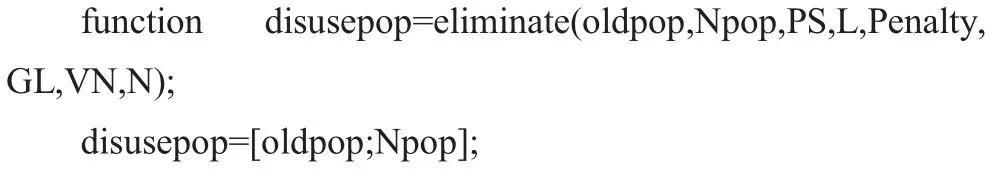

4.7 降序排序运算

5.数值实验
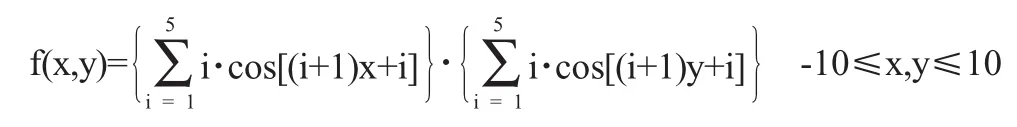

6.结论