索道桥的动力特性分析及振动控制

2011-08-08乔云强

城市道桥与防洪 2011年10期

乔云强

（林同棪国际工程咨询(中国)有限公司,重庆市 401121）

0 前言

索道桥是设有横梁稳定结构、采用高强线型材料作为主索、主要供载重车辆通行的一种悬索体系桥梁。其结构简单、重量轻,与钢筋混凝土桥和钢结构桥相比,具有建造成本低、工程周期短、便于施工、易于维修保养等特点,因此在临时工程及战备中占有重要地位，并有着广泛的应用前景。

索道桥作为非永久使用桥梁 (一般使用年限5～10 a),目前对其静力分析的工作较多，而对其动力特性的研究还很少。由于索道桥承重索应力水准较高，横断面较小，单位长度的质量亦小，桥跨弯曲刚度较低，使索道桥自振频率较低，对风荷载和车辆荷载等动力作用较敏感。而索道桥自振频率的精确理论计算是比较繁琐的，参考文献[1]给出了一种近似的计算方法。为更加精确的分析索道桥的动力特性，本文通过建立积石峡索道桥有限元模型，计算其自振特性。通过拟加4种类型的抗风索，研究不同形式抗风索的减振效果。并通过增加抗风索索力，得出索力对自振频率的影响。

1 工程概况

积石峡索道桥是为积石峡水电站砂石加工系统成品骨料运输而修建的临时性桥梁，设计车道为单车道，最大荷载40 t，使用期6 a。全桥总长180 m,索鞍之间净跨166 m,车道净宽4.5 m，主索分布宽度14 m，横梁节间距8.3 m布置.主索恒载垂度3.24 m,工作垂度4.15 m.全桥共设52束（每束3根Φ15.2钢绞线）主索，其中桥面索36束，稳定索在桥面索两侧各设8束。主索支撑于桥头索鞍上，两端通过OVM锚具与左、右岸重力式锚墩联结。积石峡索道桥结构见图1。

图1 积石峡索道桥

2 有限元法动力分析

2.1 计算方法和有限元空间模型的建立

桥梁结构的几何形状、荷载条件、边界条件、材料性质等是很复杂的,在对桥梁进行结构动力特性分析时,通常不能得出精确的理论解,而有限元法是解决这一问题的有效方法。在进行结构动力分析时,需要建立结构的刚度矩阵和质量矩阵。在建立单元刚度矩阵时,是用节点位移通过形函数来描述单元内各点的位移。质量矩阵根据研究的需要,一般有集中质量矩阵和一致质量矩阵。采用后者可以得到更精确的振型。

一般的结构动力方程为

求结构物的自振特性时,常忽略阻尼的影响。[C]=0、{F}=0，则得到结构的无阻尼自由振动方程

其特征方程(即频率方程)为

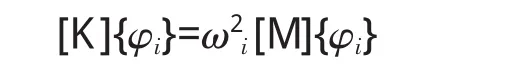
其中：[K]为刚度矩阵，{φi}为第i阶模态的振型向量（特征向量），ωi为第阶模态的固有频率（ω2i是特征值），[M]为质量矩阵。

对于求解大型结构的特征值问题,目前常用的是子空间迭代法,其基本思路就是把Reyleigh-Ritz法和逆迭代法结合起来，既利用Reyleigh-Ritz法来缩减自由度，又在计算过程中利用逆迭代法使振型逐步趋近其精确值。由于它吸收了两个方法的优点，因而计算效果比较好。

基于大型有限元软件ANSYS平台建立了该桥的有限元计算模型,在该空间模型中,主索和抗风索等效为空间杆单元(Link10单元)，对桥面索和稳定索按钢横梁的间距进行离散；钢横梁处理成梁单元(Beam188单元)；桥面铺装和栏杆只计入其质量而未计入其刚度。

根据结构设计图纸,耦合了主索与钢横梁搭接处的横桥向和竖向自由度,主索索鞍处约束其横桥向和竖向自由度，主索与抗风索锚固端为完全固结。

2.2 计算结果及分析

首先进行成桥状态下的结构非线性静力分析,然后将静力计算结果导入模态分析中，以计入索初张力对索道桥刚度的贡献。采用子空间迭代法求出该桥前30阶自振频率和振型,表1中列出了该桥前9阶频率和振型特性,限于篇幅本文只给出前3阶振型图,见图2～图4。

表1 未加抗风索前9阶自振特性

图2 一阶对称侧向振动

图3 一阶对称竖向振动

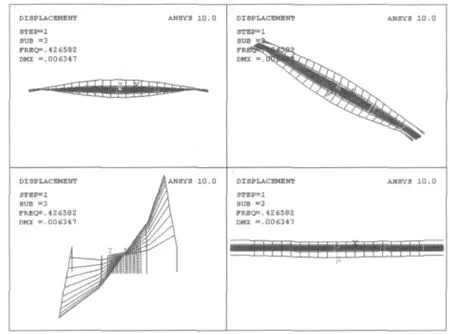
图4 一阶对称扭转振动

从表1和前3阶振型图可以看出,该索道桥的自振特性具有下列特点:

该类桥的振动特性明确，各类振型基频较低。侧向振动、竖向振动、扭转振动三种振型相继出现。侧向振动和竖向振动在相同阶振型频率较接近。

由于该桥稳定索分布宽度较大，使扭转振动基频较侧向与竖向振动基频稍大。

一般索道桥最容易产生的是扭转振动，而且扭转振动能使稳定索产生较大的振动增值，故索道桥应尽量避免大的扭转振动。

3 抗风索的形式对索道桥动力特性的影响

索道桥的振动控制主要是通过采取机械措施（抗风索）提高全桥的整体刚度。根据抗风索与索道桥面系之间的相对位置关系的不同，抗风索的形式可设计如图4所示的四种类型：平行式、外张式、内收式、交叉式抗风索。

为了比较不同的抗风索形式对索道桥自振特性的影响，拟在积石峡索道桥上分别设置上述四种抗风索系统。抗风索上端连接在跨中钢横梁的两端，下端连接在两岸的地锚上。抗风索采用Φ20 mm钢丝绳制作，张拉力采用180 kN。

图4 抗风索的形式

图5 抗风索张力与索道桥固有频率的关系

表2 不同形式抗风索系统对应索道桥的频率计算结果

表2给出了不同形式抗风索系统对应索道桥的频率计算结果，可以看出不同的抗风索构造形式对不同振型的振动频率影响差别很大。这是由于抗风索的布置形式不同产生的分力效果不同，从而对该桥各方向刚度的影响不同。如交叉式抗风索提高侧向振动频率明显，平行式抗风索提高竖向振动频率明显，外张式抗风索提高扭转振动频率明显。

4 抗风索张力对索道桥动力特性的影响

索道桥主索所受张拉力的大小影响结构自振频率，通过增加主索的张拉力来改善桥梁的动力特性往往不经济。可以通过提高抗风索张力来提高索道桥的整体刚度，降低其自振频率。为了有效说明抗风索张力与索道桥固有频率的关系，图5只给出了平行式抗风索索力变化时索道桥固有频率的计算结果。索力由180 kN增加到900 kN。

由图5可以看出索力增加对竖向振动和扭转振动的频率提高作用明显，这是因为平行式抗风索主要增加结构的竖向和扭转刚度。对侧向刚度贡献很小。推广到其他三种形式的抗风索可知，若抗风索对提高某一阶振型固有频率有效时，抗风索索力越大，该阶振型的固有频率越高。