立体车库车位分配仿真与分析
2011-08-06邢丽娟李建国
邢丽娟,李建国
(兰州交通大学机电技术研究所,兰州730070)
随着城市经济社会的发展和现代化水平的提高,我国汽车工业快速发展。其中,停车位严重不足,机动车占道停放的问题日益严重。因此,具有占地面积小,库容量大,存取车自动迅速的立体车库就应运而生[1]。
有效提高车库车位的利用率,降低耗能已成为人们广泛关注的问题之一。通过对3层×10的巷道堆垛式立体车库车位采用随机分配策略和就近分配策略,对车辆到达,库内停放时间,车位使用效率,堆垛机的运行距离等情况建立仿真模型,采用Matlab编制程序进行仿真分析,对不同分配策略采用同样参数进行数值分析。
1 模型建立
1.1 仿真模型建立原则
以库容量为30(3层×10)的车库为例进行分析,简化模型如图1。
模型的建立采用以下几种原则[2]:
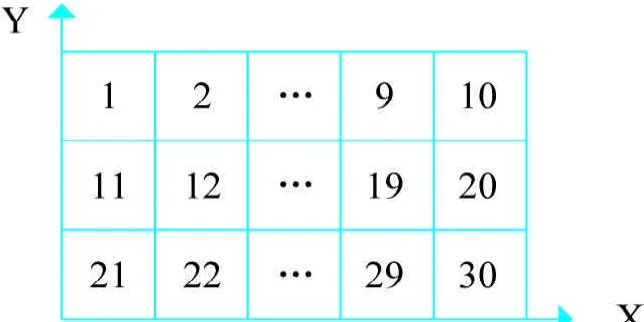
图13 层×10的立体车库简化模型
(1)临时车辆的到达时间间隔服从泊松分布;(2)临时车辆在库内存放时间服从正态分布;(3)采用就近分配策略时临时车辆车位的分配在当前可用车位中就近分配;(4)采用随机分配策略时临时车辆车位的分配在当前可用车位中随机分配;(5)临时车辆到达车库时没有可用车位则离去;(6)堆垛机在完成存取任务后在进出口点待命;(7)每次开始仿真时均认为给定的车位全部可用;(8)车库每层每列的宽度相同假设为1;(9)顾客接受服务遵循先来先服务原则(FCFS)。
1.2 相关符号说明和定义
μ:车辆在库内存放时间的期望。
σ:车辆在库内存放时间的偏差。
λ:车辆到达的时间间隔。采用Matlab[3~4]编写程序流程如图2。
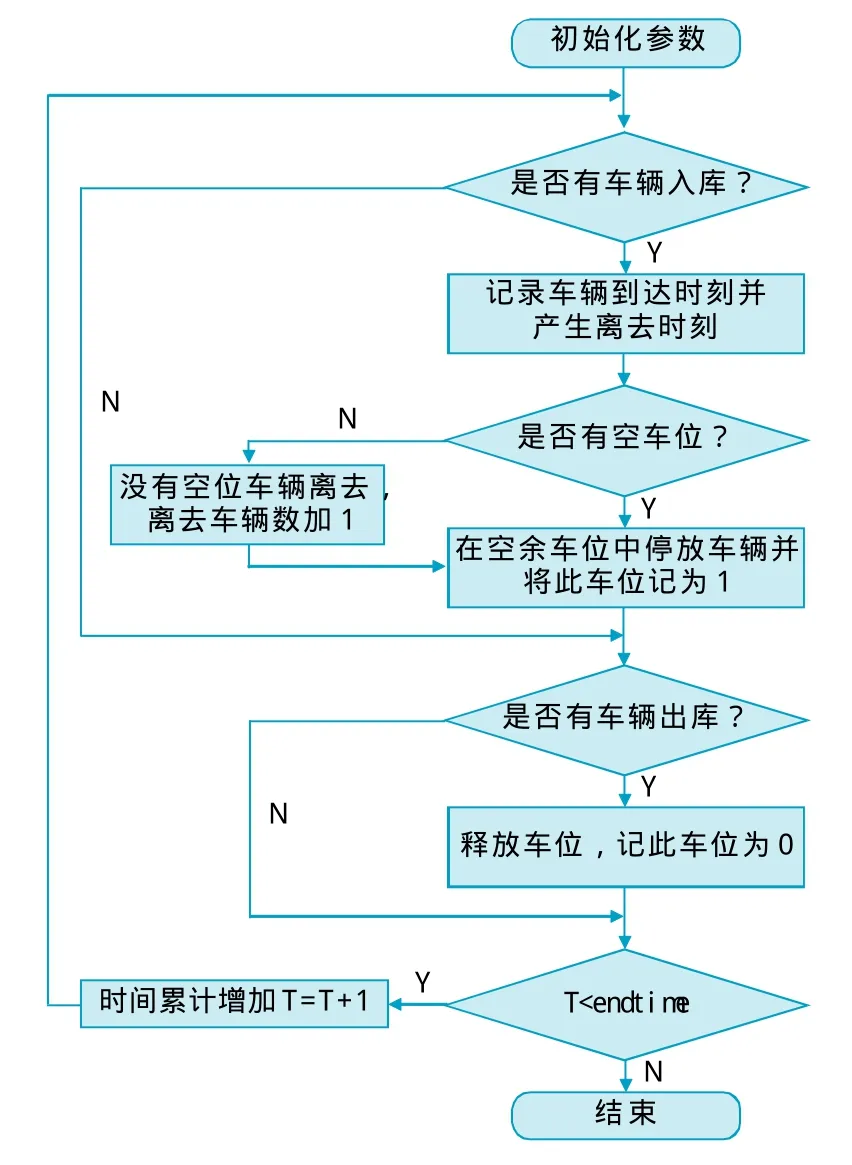
图2 程序流程图
1.3 仿真数据分析
本文以某立体停车库为例,取参数为:λ=8,μ=220,σ=30,临时停放车位数为30,仿真终止时间为1 440 min。
运行仿真程序,随机分配车位的仿真结果如图3。(a)表示车辆到达时和分配给该车辆的车位;(b)表示车辆出库时和对应车位的释放;(c)表示由于没有空余车位,车辆离去时;(d)综合a,b,c的3种情况,给出了整体的仿真结果。
就近分配车位的仿真结果如图4。
仿真结果显示,该立体停车库在某天24 h中,总共有173车次到达,170车次入库,146车次出库,3车次由于车位已满而离去。无论采用随机分配还是就近分配,车辆到达和离去的车次数是相同的。车位利用率是指在一定时间内入库的所有车辆与所有车位的比。因此,求得本次仿真的车位利用率为5.67次/车位。
为了比较随机分配和就近分配哪种分配方法较节省能量,本文还对堆垛机的运行距离编制了Matlab程序,进行了仿真分析。图5显示了随机分配原则下堆垛机每次存取车时运行的距离。当车辆出入库分别为175次和152次时堆垛机的运行总距离为1 694。
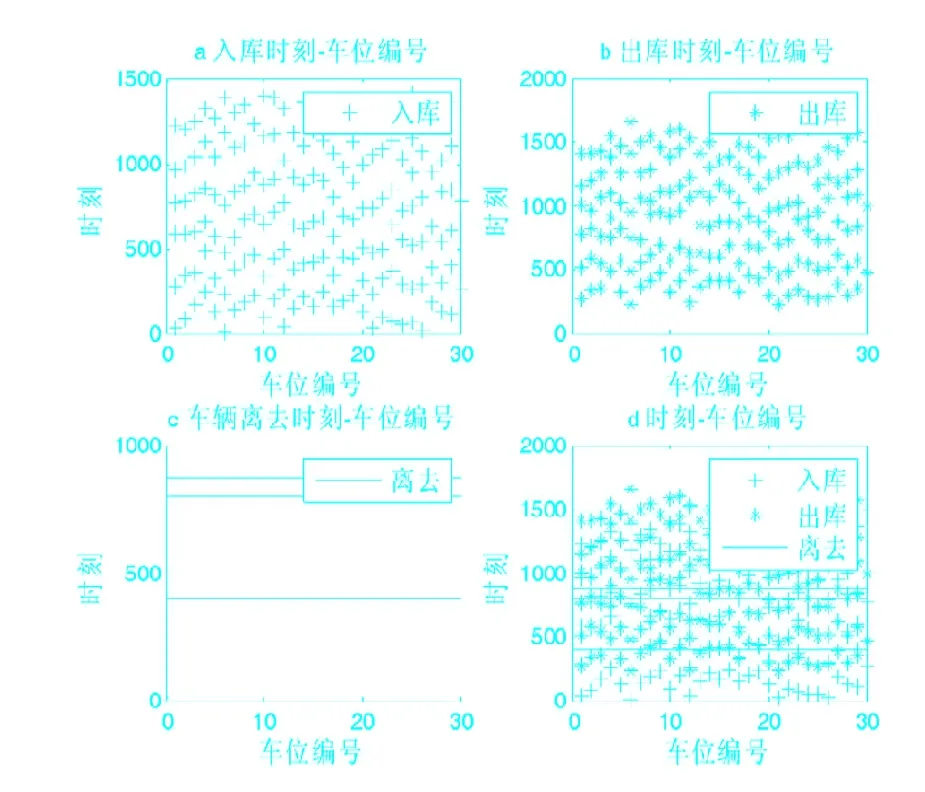
图3 随机分配车位仿真结果
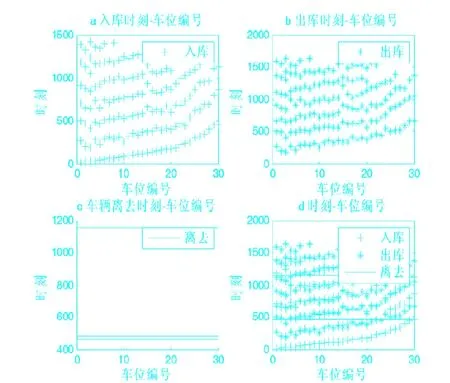
图4 就近分配车位仿真结果
图6显示了就近分配原则下堆垛机每次存取车时运行的距离。当车辆出入库分别为178次和152次时,堆垛机的运行总距离为1636。
仿真结果显示,随机分配原则下共有175车次入库,152车次出库,堆垛机的运行距离为1 694;就近分配原则下共有178车次入库,152车次出库,堆垛机的运行距离为1 636。从上面结果得出就近分配原则在出入库车次次数较多时,堆垛机的运行距离却小于随机分配原则下出入库车次次数较少的情况。 因此在本文条件下就近分配原则减小了堆垛机的运行距离达到了降低能耗的目的。
运行仿真结果100次后,堆垛机的运行距离及总距离的平均值如图7。
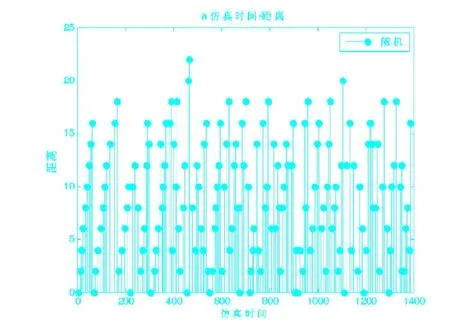
图5 随机分配车位原则下堆垛机每次存取车时运行的距离
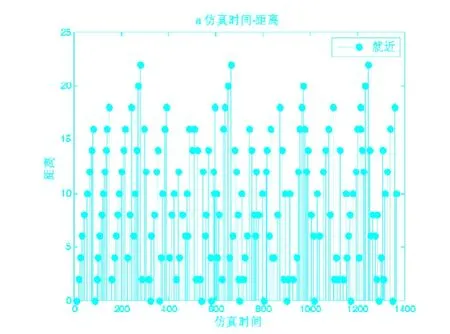
图6 就近分配车位原则下堆垛机每次存取车时运行的距离
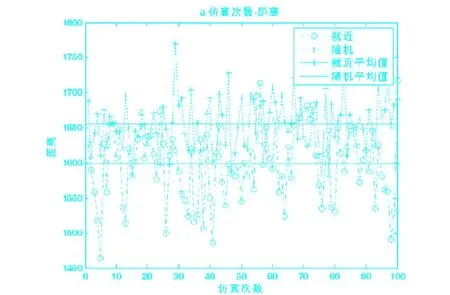
图7 就近和随机仿真100次后的平均值
从结果看,大多数情况(84次)就近分配原则下堆垛机的运行距离小于随机分配原则下堆垛机的运行距离;就近分配原则下堆垛机的平均运行距离比随机分配原则下堆垛机的平均运行距离短。从而进一步说明了在本文所取参数下就近分配原则相对减小了堆垛机的运行距离,达到了降低能耗的目的。
2 结束语
模拟仿真的结果表明就近分配策略相对减少了堆垛机的运行距离,达到了降低耗能的目的。
改变本文的参数,例如车辆入库的时间间隔、停放时间、车位数量等,可以得到不同的仿真效果,因此对建设立体车库的决策者有一定的帮助。
本文仍有不足,以下几点需要以后进一步研究:(1)结合智能算法,找到更节能的存取策略;(2)研究层列距离不相等时堆垛机的运行情况,找到较优的分配策略;(3)比较堆垛机完成一次任务后原地待命条件下的运行距离与本文运行距离的差异,找到堆垛机的较优停放点。
[1] 周雪松,田密,马幼捷,马云斌,邵宝福,王辉. 智能化立体车库存取车优化控制策略的研究[J] . 制造业自动化,2008,30(10):29-34.
[2] 李建国,蒋兆远. 巷道堆垛式立体车库随机车位分配策略仿真与分析[J] . 起重运输机械,2010(8):57-59.
[3] 周品,赵新分. Matlab数学建模与仿真[M] . 北京:国防工业出版社,2009.
[4] 曹弋. Matlab教程及实训[M] . 北京:机械工业出版社,2008.
