基于DT-CWT的图像融合算法研究

陶玲瑶，弓晓锋

（贵州大学 计算机科学与信息学院，贵州 贵阳 550025）

0 引言

图像融合是信息等融合的重要分支。基于小波变换的图像融合技术代表了当今像素级多聚焦图像融合技术的发展前沿之一。

目前常见的小波变换，一般采用简单的加权平均，或是基于区域能量的融合方法。加权平均虽然简单，但导致了融合图像的部分边缘信息被平均亮度所湮没；基于区域能量的融合准则虽然考虑像素区域之间相关性，融合效果也有所提高却忽略了图像的边缘信息，对灰度的突变反应不够敏感[1]。

双树复小波变换(DT-CWT, Dual-tree Complex Wavelet Transform)却能克服以上不足，具有优良的方向分析能力，能够反映图像在不同分辨率上沿多个方向变化的情形[2]。因此这里采用基于图像域标准差的高频融合度量，提出两种融合方式，加强融合图像的边缘信息，得到更好图像融合效果。

1 双树复小波变换的基本原理

与实小波相比，复小波变换多了一路变换，整个变换具有两个树，称为A树和B树。

从图1得出Q-shift滤波器在两树的第二层及其以后各层上均为偶数长度，但不再严格的线性相位。Q-shift是一种在满足带通滤波器的标准正交完美重构条件下，具有合适的偶数长度和1/4采样延迟的滤波器。使A树为1/4时延 (+q)，B树为3/4时延(+3q)[3]。保证在每一层上，B树采样点刚好位于A树采样点的中间，实现对称采样。

图1 一维信号的Q-shift双树复小波分解树

2 图像融合算法

2.1 图像融合步骤

图像融合步骤如下：

①将两幅源图像作双树复小波分解，得到各自的高低频域分量；

②根据高低频分量的不同特性，设计相应的融合规则并将其各自融合；

③将利用双树复小波将融合后高低频域重构出融合图像。

2.2 高频域的融合测度

高频子带反映源图像的细节信息，采用图像域的标准差作融合测度，反映各灰度值均值的离散情况，标准差越大，灰度值分布越分散，而灰度值的起伏反映了图像的纹理和边缘信息[4]。

尺度为 L、方向为ε的高频子带像素(m, n)在邻域[-k, k]的区域标准差计算式为[5]：

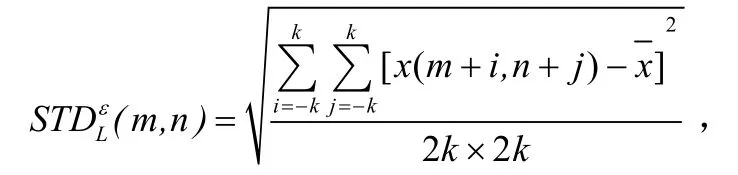
式中，x(m+i,n+j)为像素灰度值；x是当前局部区域像素灰度均值；ε=1,2,…,6，区域大小可以是 3×3, 5×5 等。

2.3 基于DT-CWT的融合算法

这里的研究选取源图像均为灰度图像，在低频域融合规则不变下，提出了高频域的两种融合方法，即方法1和方法2，并作定量比较。

Yhi和 Y li（i=1或2）分别表示两幅源图像的高低频分量，Yh和Yl则是融合图像的高低频分量。

方法1：低频域采用加权平均，高频域采用Mp阈值的加权平均融合规则，即方法1是在传统加权平均法基础上做了一定改进：

①低频域：Yl =0 .5*Yl1+ 0 .5* Yl2;

②高频域：Yh｛P｝= （ Yh1｛P｝+ Yh2{P}）/MP，

式中，Mp为对应小波分解层的高频分量阈值，现选取p=3。

方法 2：对低频域加权平均，高频域采用标准差融合测度；

①低频域：Yl=0.5*Y l1+ 0.5* Yl2;

②高频域：设 S TD1(m,n)，S TD2(m,n)的DT-CWT分解层数选为3，每层分解有6个方向，由上述区域标准差公式可知，L=1，2，3，ε=1，2，…，6，图像区域大小是 32×32,64×64 等。

式中 Yh{L} = (∶,∶,ε)表示当DT-CWT分解为第L层第 ε个方向时的对应高频分量，K1，K2表示此时所取的相应阈值，取值方式同方法2中的低频域规则相似：

式中，a=STD1(m,n )- STD2(m,n),高频域均为复数形式，在DT-CWT分解后的 3层分量分别为：128×128,64×64,32×32。每一层每一方向的像素点矩阵中每一元素都计算标准差，利用上式确定出 K1，K2值，融合相应像素点的高频域，保证了在融合时选取标准差较大的像素，进而加强融合图像的边缘信息。

3 两种融合方法比较

3.1 仿真实现

这里主要采用3层双树复小波变换形式，并在此基础上，分别对高低频融合规则作进一步研究，如图2和图3所示。

图2 灰度多聚焦源图像A、B

图3 两种融合方法的结果比较

3.2 融合结果定量评价

将以上两种方法的实验结果进行了定量比较。融合评价方法使用了传统的熵、总体交叉熵、通用的主观和客观因素相结合的图像融合评价方法（Q，QW和QE）。

根据源图像A，B及融合图像F这三者的关系，得出其结构相似度[6]：

在 Q (A ,B,F)中，源图像A,B中每个窗口的贡献都是对等的，可以对每个窗口赋予不同的权值：

从而可定义加权的融合质量评价指标：

此外,对边缘信息的特性等，用梯度范数 A’代替源图像中的灰度值A，得到相应的 Q (A ,, B ,, F , )，从而得到基于边

W缘的评价指标：

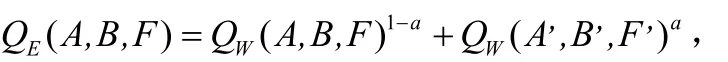
式中，a表示边缘图像对原始图像的贡献，其值越大，边缘图像的贡献越大。

综上所述，熵值越大，总体交叉熵的值越小，说明融合效果越好，而且通用评测方法中的3个指标Q，QW，QE值均在[0，1]之间，值越接近 1，表示融合质量越高，如表 1所示。

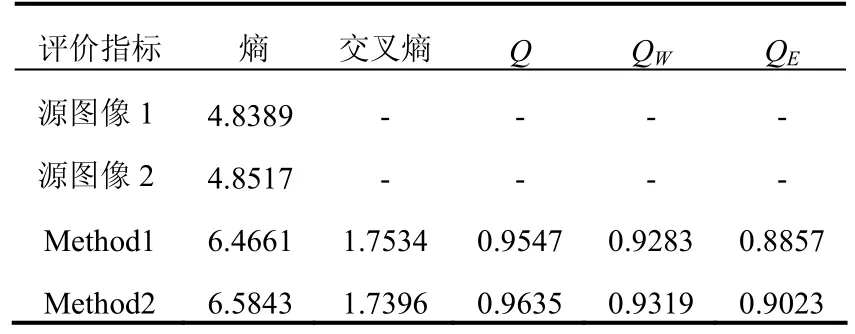
表1 图像融合性能评价

从表1可看出，Method2的总体交叉熵略小于Method1，而图像交叉熵直接反映两幅图像对应像素的差异，可以用来确定各种融合效果的优劣，交叉熵值越小，说明融合结果图像与两幅原始图像的差异越小。Method2融合图像的主客观因素相结合的评测方法的3个指标都略高于Method1融合图像，更接近于1。以上各实验数据均表明Method2融合规则优于 Method1。所以，高频域采用标准差测度后，使得融合图像的各项性能参数达到较好的水平，提高了边缘信息和纹理特征。

4 结语

文中采用双树复小波变换法，克服了传统离散小波变换在图像分解和重构中带来的移变性等不足。在融合规则上，注重高频域融合算法的研究，采用图像区域标准差作为融合测度，并作了相应的定量融合性能评价，如信息熵，交叉熵以及通用的主客观相结合的测评方法。

这里的研究主要针对高频分量的图像规则改进，尚未对低频分量做出较好的算法改进，所以有待在今后的工作中，对低频域加以深入的研究，使得图像融合具有更广泛的应用和更好的实际价值。

[1] 宋谨, 石霏. 基于双树复小波变换的多聚焦图像融合算法研究[J].现代电子技术, 2010, 33(02):6-8.

[2] 范鹏,田间,何登平.一种基于小波变换的自适应数字水印算法[J].通信技术, 2007, 40(11) :4-5.

[3] 覃焕昌, 滕政胜. 基于正交小波变换的图像去噪算法研究[J]. 通信技术, 2009, 42(01) :3-5.

[4] 侯阿临, 王楠, 张志芳,等. 基于双树复小波变换的CT与MRI图像融合算法[J]. 电视技术, 2008, 32(z1) :11-13

[5] LI M X, MAO H P, ZHANG Y C. Fusion Algorithm for Multi-sensor Images based on PCA and Lifting Wavelet Transformation[J].New Zealand Journal of Agricultural Research, 2007, 50(05):15-27.

[6] 杨伟,柴奇,王黎明.基于双树复小波变换的多聚焦图像融合方法[J].光电技术应用, 2009, 24(03) :5-11.