基于遗传算法的通风网络两步法风流调节优化算法

厍向阳 ，常新坦，孙艺珍

(1. 西安科技大学 计算机科学与技术学院，陕西 西安，710054；2. 西安科技大学 西部矿井开采及灾害防治教育部重点实验室，陕西 西安，710054)

随着矿井开采向深度、广度扩展和机械化程度不断提高，矿井通风网络安全运行、维护和管理成本不断增加，通风网络优化研究与应用的重要性日渐凸现出来。矿井通风网络可分为自然分风网络、控制型分风网络和混合型分风网络3类。已经证明，在满足矿井总风量要求的条件下，自然分风网络的功耗自动达到最小[1-3]。在控制型分风网络中，各分支的风阻和风量已知，其风压也自然确定，这种网络的优化与调节问题是一个线性规划问题，求解方法有单纯形法、关键路径法、回路法和道路法等[3-5]。自然分风网络解算、控制型分风网络优化目前已经得到较好解决。混合型通风网络优化模型是一个非凸规划模型，目前还没有可靠的求解方法。由于调节设施的位置待定，通风网络优化模型变量数目非常大。因而混合型通风网络优化模型的求解十分困难，成为目前研究的重点和难点。文献[4, 6-10]研究用非线性规划的方法来解决矿井通风网络优化调节问题，但存在函数求导、矩阵求逆、初始值敏感和算法效率低的缺陷。文献[1, 11]将通风网络优化问题分解为风量最优分配和最优调节2个子问题,并给出了求解风量最优分配问题的非线性规划数学模型和求解方法。这种方法减少了非线性规划问题的规模, 对于混合型通风网络的优化调节具有一定的理论和实际意义，由于风量分配优化模型仍然为非凸、非线性优化模型，同样存在传统非线性规划的方法缺陷。李湖生[12]介绍了 1995年以前矿井按需分风优化调节方面的研究进展，分析了各种方法的特点和局限性，具有重要的参考意义。张玉祥等[13-16]将遗传算法引入到通风网络优化中，取得了一定成果，但是未能将遗传算法与通风网络理论、图论和矿井实际密切结合，未能很好地解决调风地点约束和大规模通风网络优化问题。在此，本文作者概括了混合型通风网络优化的模型，归纳了混合型通风网络风量最优分配和风流最优调控两步法优化基本框架。首先，在满足矿井通风风量需求的基础上，实现风量分配优化或者自然分风子网进行自然分风计算。然后，结合矿井通风网络实际调风需求，引入遗传算法随机产生动态网络的邻接矩阵，使用附有条件的最小支撑树算法求解部分余树弦(调风地点)约束下的最小支撑树和独立回路矩阵，计算通风网络分支风阻调节值，在通风总功率和约束条件基础上构建广义最小化目标函数，依此对调节方案进行评价，使用遗传算法中的进化算子对调节方案编码实施进化操作，最终得到满意解。最后通过典型通风网络实例测试算法的可行性和有效性。

1 通风网络优化模型

对于矿井通风网络G＝(V,E)，V和E分别为图G的结点和分支集合，且|V|=m，|E|=n，分别为网络G中结点和分支数，通风网络的独立回路个数b=n-m+1，k条边风量已知，且k≤b。通风网络优化模型如式(1)～(6)所示。

式中：rj为第j分支的风阻；qj为第j分支的风量；F为安置风机(包括主扇和辅扇)分支标号集合；Δhj为第j分支的阻力调节值；hj为第j分支风压；hNj为第j分支内位能差，亦自然风压；qj-min为第j分支允许风量下限；qj-max为第j分支允许风量上限；Δhj-min为第j分支允许风压调节下限；Δhj-max为第j分支允许风压调节上限；{cij}为基本回路矩阵；{bij}为基本关联矩阵。

式(1)为优化目标函数，式(2)为风量平衡约束条件，式(3)为风压平衡约束条件，式(5)和式(6)为风量和风压调节上、下限约束。当某一分支风量已知时，则式(5)约束变成为qj-min=qj=qj-max。当某一分支不允许安设调风设施时，则式(6)约束变成为Δhj-min=Δhj=Δhj-max=0。故式(5)和式(6)包含通风网络分支风量是否已知和调风地点约束条件。

模型(1)～(6)中的决策变量为余树弦中未知风量分枝的qj(共b-k=n-m+1-k个)和n个分支的Δhj。由理论分析可知：(1) 该模型是一个非凸规划模型，目前还没有可靠的求解方法；(2) 调节设施的位置待定，整个网络中有n个未知的阻力调节值变量，使得该模型的变量个数非常大。对于非线性规划问题，即使能解，其算法效率也会随着变量个数的增加而急剧降低。欲获得实际可行的模型和算法，应该一方面使模型凸性化，另一方面尽量减少变量数目。

2 混合型通风网络两步法优化的基本框架

针对矿井通风生产实际特点，结合通风网络理论、最优化理论，可将混合型通风网络优化问题简化为混合型通风网络风量最优分配和混合型通风网络风流最优调控2个子优化问题，分别进行优化就可达到混合型通风网络优化的目的，将这一方法称为混合型通风网络两步法优化方法，基本框架如图1所示。

2.1 混合型通风网络风量最优分配

在风量平衡、部分分支风量已知的约束条件下，风量分配方案对目标函数的贡献取决于分风方案对应的支撑树的选取方案和余树弦风量的大小。理论上已经证明，在满足矿井总风量要求的条件下，自然分风网络的功耗自动达到最小。因此，可以对通风网络中自然分风分支组成的子网实现自然分风计算，可采用牛顿法、拟牛顿法、斯考特-恒斯雷法、京大一试法、拟线性解法等方法求解，这些方法理论严密，求解方便，但存在函数求导，矩阵求逆，对初始值敏感等缺陷。另外一个方法是将混合型通风网络风量最优分配转化为一个优化问题[1]，该模型和混合型通风网络优化模型相比，由于暂时没有考虑调风问题，变量数目大大减少，但仍是一个非线性优化问题，求解仍有一定难度。

2.2 混合型通风网络风流最优调控

在满足风压平衡、调风地点约束约束的条件下，以网络运行功率最小化作为目标函数，对通风网络调风进行优化。通风网络风流调控有许多成熟的方法，如单纯形法、关键路径法、回路法和道路法等。这些方法求解方便快捷，基本上能够满足生产实际需求，但是，在最优调控算法和处理调风地点约束的优化方面不完善。

3 基于遗传算法的通风网络两步法风流调节优化算法

3.1 基本思想

按照混合型通风网络两步法优化的基本框架，首先进行混合型通风网络风量分配优化或混合型通风网络子网自然分风解算，求得混合型通风网络分支风量。然后将遗传算法与通风网络回路法风流调节算法相结合进行混合型通风网络风流最优调控。

图1 混合型通风网络两步法优化的基本框架Fig.1 Basic frame of two step way on mixing ventilation networks optimization

在满足风压平衡、调风地点约束约束的条件下，风流调控方案对目标函数的贡献取决于调风方案对应的支撑树的选取方案和余树弦风压调节值。在限定调风地点约束条件下，调风用最小支撑树必须需满足限定的调风分支在余树弦上。为了获得通风网络风流最优调控方案，可以对满足限定余树弦约束的所有支撑树进行遍历，通过比较目标函数值而得到最优方案。对于一般的矿井，通风网络的规模都会比较大，遍历的方法显然是不可取的。引入遗传算法随机产生多组调控方案，每一个方案对应一个动态邻接矩阵(仅仅改变通风网络结点的距离，不改变结点间的邻接关系)。使用动态网络条件下最小支撑树算法，求解每组相应的附有条件的最小支撑树[17]及其对应回路矩阵。根据回路矩阵计算通风网络风压调节值。基于通风总功率和约束条件构建广义最小化目标函数[18]，依此对每个通风网络风量调控方案进行评价。通过遗传算法中的进化操作算子对每个风量调控方案的编码进行进化操作[19]。最终得到最优的风流调节方案。

3.2 基于遗传算法的通风网络两步法风流调节优化算法

(1) 算法：基于遗传算法的通风网络两步法风流调节优化算法。

(2) 输入：通风网络的分支风量，风阻对应的邻接矩阵，分支调节阻力上、下限。

(3) 输出：输出分支风阻调节值和最优目标函数值。

(4) 方法：

Step 1 设置GA相关参数，包括最大迭代次数、群体大小、交叉概率、变异概率。

Step 2 群体初始化。使用计算机随机产生规定规模的染色体群体。染色体群中每一串染色体对应通风网络调风用的随机邻接矩阵。

Step 3 染色体解码。根据通风网络调风用的随机邻接矩阵，求解对应的附有条件的最小支撑树及其相应独立回路矩阵CH。按照下式进行通风网络调风计算：

式中：ΔHY为余树弦的阻力调节值向量，HY为余树弦的阻力向量，为树枝的阻力向量，为独立回路矩阵CH中由与树枝对应的列组成的子矩阵，为独立回路矩阵CH中由与余树枝对应的列组成的子矩阵，为单位方阵；PC为通风网络独立回路所含的通风能量和矩阵，。

Step 4 群体评价。按照下式计算广义目标函数值，依此对染色体群体进行评价。

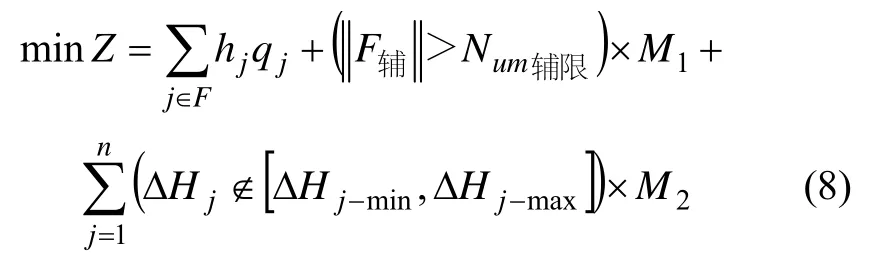
Step 5 染色体选择。依据评价结果，选择较优的染色体，进行下一步操作。

Step 6 染色体交叉。

Step 7 染色体变异。

Step 8 染色体保留。

Step 9 中止条件检验。如果小于最大迭代次数，则转向Step 3，否则停止迭代，输出分支风阻调节值和最优目标函数值。

4 通风网络优化实例

4.1 简单通风网络优化调控

某一通风网络如图2所示[1,5]，通风网络有10个结点，16条弧，圈起来的数字为通风网络分支标号，未圈起来的数字为通风网络结点标号。通风网络分支编号和分支风阻见表1第1列和第2列。通风网络中自然分风分支组成的子网实现自然分风计算，计算结果见表1中第3列。

图2 简单通风网络图Fig.2 Simple ventilation networks figure

方案1：主扇安置在分支e1，Δhj＜0(主扇除外)，亦不允许安置副扇，调风地点没有限制。

方案2：主扇安置在分支e1，Δhj＜0(主扇除外)，亦不允许安置副扇，分支e7禁止安置调风设施。

方案3：主扇安置在分支e1，允许安置1台副扇，Δhj∈(-50, 50) (主扇除外)，调风地点没有限制。

方案4：主扇安置在分支e1，允许安置1台副扇，Δhj∈(-50, 50) (主扇除外)，分支e14禁止安置调风分设施，分支e9不允许安置副扇。

遗传算法的染色体群体规模为30，交叉概率0.8，变异概率为0.05，迭代100次后的结果如表1所示。经过检验计算，表1中所有方案满足通风网络结点风量平衡、独立闭合回路风压闭合和调风地点约束条件。

4.2 多风机通风网络优化调控

某一通风网络如图3所示[5]，有35个结点，55条弧。通风网络分支编号和分支风阻见表2中第1列和第2列。通风网络中自然分风分支组成的子网实现自然分风计算，计算结果见表2中第3列。

图3 多风机通风网络图Fig.3 Multiple-fan ventilation networks figure

表1 简单通风网络优化调控结果Table 1 Results of ventilation optimization adjustment on simple ventilation networks

表2 多风机通风网络优化调控结果Table 2 Results of ventilation optimization adjustment on multiple-fan ventilation networks

方案1：3台主扇分别安置在分支e18，e31和e50，Δhj＜0(主扇除外)，亦不允许安置副扇，调风地点没有限制。

方案2：3台主扇分别安置在分支e18，e31和e50，Δhj＜0(主扇除外)，亦不允许安置副扇，分支e28禁止安设调风设施。

方案3：3台主扇分别安置在分支e18，e31和e50，1 台副扇，Δhj∈(-50, 50) (主扇除外)。

方案4：3台主扇分别安置在分支e18，e31和e50，1台副扇，Δhj∈(-50, 50) (主扇除外)，分支e22不允许安置副扇。

4个方案的染色体群体规模为30，交叉概率0.8，变异概率为0.05，迭代100次后的结果如表2所示。经过检验计算，4个方案满足通风网络优化模型(1)～(6)中的约束条件。

从实验结果分析可得：(1) 该算法可以满足生产实际中混合型通风网络优化的特定要求；(2) 在某一特定的通风网络中，科学合理的增加副扇数量，会降低能耗，但增加了通风网络日常风机管理复杂程度，在矿井灾变时期，通风网络调控难度增加；(3) 增加额外调风附加约束条件是以增加通风网络额外的能耗为代价。

5 结论

(1) 两步法思想把混合型通风网络优化问题转化为通风网络风量分配优化和通风网络调控优化两个问题，大大减小优化模型的变量数目，提高了算法的效率。

(2) 该方法把遗传算法和通风网络回路法风流调节有机结合，发挥各自优势，弥补了各自的缺陷。

(3) 该方法可以方便地解决调风地点约束的通风网络优化求解问题。

(4) 通过简单通风网络优化和多风机通风网络优化实例的多个方案的测试和正确性验证，表明该算法可按照生产需求实现对通风网络的优化调控，具有一定的有效性、可行性和实用性。

(5) 只要通风网络的优化模型理论上有解，本算法均可进行通风网络优化。

[1] 王惠宾. 矿井通风网络理论与算法[M]. 徐州: 中国矿业大学出版社, 1996: 97-100.WANG Hui-bin. Theory and algorithm of mine ventilation network[M]. Xuzhou: China University of Mine and Technology Press, 1996: 97-100.

[2] Hartman H L. Mine ventilation and air conditioning[M]. New York: John Wiley & Sons, 1982: 483-516.

[3] 徐竹云. 矿井通风系统优化原理与设计计算方法[M]. 北京:冶金工业出版社, 1996: 107-128.XU Zhu-yun. Optimization theory and computing method of mine ventilation[M]. Beijing: China Metallurgical Industry Press,1996: 107-128.

[4] 陈开岩. 矿井通风系统优化理论及应用[M]. 徐州: 中国矿业大学出版社, 2003: 71-87.CHEN Kai-yan. Optimization theory and application of mine ventilation[M]. Xuzhou: China University of Mine and Technology Press, 2003: 71-87.

[5] 李恕和. 矿井通风网络图论[M]. 北京: 煤炭工业出版社,1984: 112-133.LI Shu-he. Mine ventilation network graph theory[M]. Beijing:China Coal Industry Publishing House, 1984: 112-133.

[6] HU Wei-min, Longspn I. A computer method for the generalized controlled flow problem in ventilation networks[J]. Mining Science and Technology, 1989, 8(2): 153-168.

[7] Ueng T H, Wang Y J. Analysis of mine ventilation networks using nonlinear programming techniques[J]. International Journal of Mining Engineering, 1984, 3(2): 245-252.

[8] 卢新明. 非线性管道网络中的数学规划问题及解法[J]. 应用数学学报, 1989, 12(3): 281-291.LU Xin-ming. Mathematical programming problems in nonlinear pipeline networks and their solutions[J]. Acta Mathematicae Applicatae Sinica, 1989, 12(3): 281-291.

[9] XU Zhu-yun, WANG Yin-min. Study on optimum ventilation networks using nonlinear programming techniques[C]//Proceedings of 5th US Mine Ventilation Symposium. Morganton:West Virginia University, 1991: 440-444.

[10] HUANG Chang-hong, Wang Y J. Mine ventilation network optimization using the generalized reduced gradient method[C]//Proceeding of the 6th US Mine Ventilation Symposium. Salt Lake City: University of Utah, 1993: 153-161.

[11] 黄元平, 李湖生. 矿井通风网络优化调节问题的非线性规划解法[J]. 煤炭学报, 1995, 20(1): 14-20.HUANG Yuan-ping, LI Hu-sheng. Solution of problems relevant to optimal control of mine ventilation network by non-linear programming technique[J]. Journal of China Coal Society, 1995,20(1): 14-20.

[12] 李湖生. 矿井按需分风优化调节的研究进展[J]. 矿业安全与环保, 1997, 24(1): 8-11.LI Hu-sheng. Development of optimized regulation of air distribution according to demand in mine[J]. Mining Safety &Environmental Protection, 1997, 24(1): 8-11.

[13] 张玉祥, 杨昌玲. 快速模拟退火算法及矿井通风网络全局优化[J]. 武汉工业大学学报, 1998, 20(1): 40-42.ZHANG Yu-xiang, YANG Chang-ling. A fast simulated annealing algorithm and its application to global optimal design of ventilation network in mine[J]. Journal of Wuhan University of Technology, 1998, 20(1): 40-42.

[14] 钟茂华, 陈宝智. 基于遗传算法的矿井火灾时期风流优化控制[J]. 煤炭学报, 1998, 23(2): 161-164.ZHONG Mao-hua, CHEN Bao-zhi. Optimal control of airflow in a mine fire based on genetic algorithm[J]. Journal of China Coal Society, 1998, 23(2): 161-164.

[15] 王战权, 赵朝义, 云庆夏. 用遗传算法进行通风系统优化的研究[J]. 矿业安全与环保, 1999, 22(6): 6-8.WANG Zhan-quan, ZHAO Chao-yi, YUN Qing-xia. Research on optimization of ventilation system by genetic algorithm[J].Mining Safety & Environmental Protection, 1999, 22(6): 6-8.

[16] 李江, 陈开岩, 林柏泉. 遗传算法在矿井通风网络优化中的应用[J]. 中国矿业大学学报, 2007, 36(6): 789-793.LI Jiang, CHEN Kai-yan, LIN Bai-quan. Genetic algorithm for optimization of mine ventilation network[J]. Journal of China University of Mining & Technology, 2007, 36(6): 789-793.

[17] 厍向阳, 罗晓霞. 附有条件的最小支撑树算法[J]. 西安科技大学学报, 2008, 28(4): 771-774.SHE Xiang-yang, LUO Xiao-xia. Minimum spanning tree algorithm confined in conditions[J]. Journal of Xi’an University of Science and Technology, 2008, 28(4): 771-774.

[18] 陈宝林. 最优化理论与算法[M]. 2版. 北京: 清华大学出版社,2005: 394-413.CHEN Bao-lin. Optimization theory and algorithms[M]. 2nd ed.Beijing: Tsinghua University Press, 2005: 394-413.

[19] 玄光男, 程润伟. 遗传算法与工程优化[M]. 于歆杰, 周根贵,译. 北京: 清华大学出版社, 2004: 1-9.XUAN Guang-nan, CHENG Run-wei. Genetic algorithms and engineering optimization[M]. YU Xin-jie, ZHOU Gen-gui,translate. Beijing: Tsinghua University Press, 2004: 1-9.