长流程生产过程多重大时滞系统时间协调参数自调整控制策略

喻寿益，钟柳芳，桂卫华，谢永芳

(中南大学 信息科学与工程学院，湖南 长沙，410083)

长流程工业生产通常是由多个不同的生产工序完成的，各种工序的生产设备地域跨度大，工艺流程长。原料从生产工序入口处输入，从工序出口处输出产品(或中间产品)。从入口到出口，物料传质输送和完成物理化学反应往往需要几十分钟，甚至几小时。为了满足工艺指标的要求，保证产品质量，在工序生产设备的不同部位，设置多个控制点。不同控制点到工序出口处的距离不同，物料传质所需要的时间也不同，这样使不同控制点的控制量到出口处产品的输出量产生不同的时间延迟τ1，…，τn，而这些纯延迟时间往往是系统响应时间常数T的几倍甚至十几倍，这样的工序生产过程构成多重大时滞系统。多重大时滞特性严重影响系统的控制性能，降低控制精度，不同控制变量的设定值难以协调跟踪，闭环控制系统往往不能稳定运行。例如氧化铝生产过程的高压溶出工序和连续碳酸化分解工序，都是多重大时滞系统。通常补偿时滞影响的方法有 Smith预估算法[1-3]、自适应控制[4-6]、智能控制[7-9]、模糊控制[10-12]、H∞控制[13-15]等。其中：Smith预估算法的控制效果严重依赖于被控对象的精确数学模型，预估器模型与被控对象的偏差会使系统控制性能恶化，在实际应用中往往难以取得理想的控制效果。自适应参数调整方法[4-6]只对预估器参数进行了部分调整，但实际控制对象任意一个参数的改变，特别是纯延迟时间的变化会严重影响系统的控制性能；模糊控制[10-12]整定起来较复杂，不利于实时调整。对于多重大时滞系统实际应用有效的控制算法很少见于报道。在此，本文作者提出一种基于脉冲响应等效系统的多重时间协调参数自调整(M-TCPA)控制策略，由多个TCPA控制器保证各个控制点的控制精度，实现系统闭环稳定运行。通过设定值校正和工艺指标调整开关，实现各个控制变量设定值协调跟踪，满足整个生产工艺指标要求。在此，本文作者分析TCPA控制策略和系统稳定性，研究多重大时滞控制系统结构和工作原理。

1 TCPA控制策略工作原理

1.1 脉冲响应等效系统

设大时滞系统G1和G2的纯延迟时间τ=dTs相等，若它们的脉冲响应函数g1(t)和g2(t)的系数之和相等，则称系统G1和G2是脉冲响应等效系统。对于2个脉冲响应等效系统G1和G2，若它们的输入信号相同且为阶跃信号，则它们的输出信号总是相等的，如图 1所示。

证明：设系统G1和G2的延迟时间为d，输入信号是阶跃信号U(t)，则系统G1在k时刻的输出。

系统G2在k时刻的输出y2(k)=，由假设条件可知，证毕。

图1 等效系统的脉冲响应曲线Fig.1 Curves of pulse response equivalent system

1.2 TCPA控制策略

大时滞系统时间协调参数自调整(TCPA)控制策略由2部分组成：① 根据被控对象输出误差，通过时间协调原则，修正控制器的输出；② 将脉冲响应等效系统输出与设定值比较，根据误差修正脉冲响应等效系统和控制器的参数。

1.2.1 时间协调(TC)原则

大时滞被控对象输出误差为：

式中：yr(k)为设定值；y(k)为对象输出检测值。k时刻控制器输出修正量为：

式中：为脉冲响应等效系统的脉冲响应系数。设(k-d-N)时刻至(k-d- 1 )时刻控制器输出都是合适的，使(k-1)时刻以前被控对象的输出误差都在允许值范围之内。k时刻对象输出误差主要是由u((k-d-1)不合适引起的，需要修正，以便使(k+d-1)时刻对象输出误差控制在允许范围之内，得到：

k时刻控制器输出是以(k-d-1)时刻控制器输出为参考进行修正的，时刻的选择由纯延迟时间d决定，故称为时间协调原则。将控制器输出信号u(k)同时输入到脉冲响应等效系统，并存储用以计算脉冲响应等效系统的输出。

1.2.2 控制器参数调整(PA)

脉冲响应等效系统k时刻输出为：

TCPA闭环控制系统框图如图2所示。图2中：控制器输入信号为大时滞系统k时刻输出误差Δy(k)，控制器输出u(k)按式(3)调整。同时u(k)输入脉冲向量U(k-d-1)存储器，用以计算脉冲响应等效系统输出。脉冲响应等效系统参数的修改按式(5)进行，其目的是调整控制器的参数。

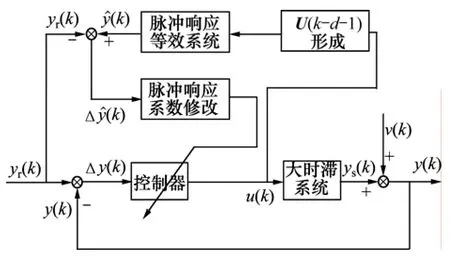
图2 TCPA控制系统原理图Fig.2 Principle block diagram of TCPA control system

当TCPA控制系统达到稳定状态时，脉冲响应等效系统的脉冲响应系数之和和被控对象的脉冲响应系数之和相等。在设定值不变的条件下，控制器输出信号u(k)同时输入到脉冲响应等效系统和大时滞系统，它们的输出相等。根据内模控制系统对偶稳定性原理，在控制器和大时滞系统都是稳定的条件下，只要大时滞系统和脉冲响应等效系统完全匹配，则闭环系统就是稳定的。因此，TCPA控制系统是稳定的。

1.2.3 TCPA控制算法仿真

使用Simulink仿真软件对TCPA控制算法和PID控制算法进行对比仿真研究。取被控对象为一阶惯性加纯滞后环节，其模型为，参数K=1.45，T=45，延迟时间τ分别为50 s和200 s，采样周期为2.5 s。将PID控制算法的参数Kp，Ti和Td在较宽的范围内选择配合，Kp从0.1至0.75，Ti从15至90，Td从1至15，进行大量的仿真。当τ为50 s时，PID控制算法阶跃响应曲线都会出现大幅度超调并有一定振荡，对扰动的调整时间长。随τ增大，其动态特性明显变差，当τ为200 s时，不管PID参数如何选择，都会出现振荡。从仿真结果中选取典型的仿真曲线，如图3和图4所示。

图3 τ为50 s时仿真曲线Fig.3 Simulation curves when τ is 50

图4 τ为200 s时仿真曲线Fig.4 Simulation curves when τ is 200

图3所示是延迟时间τ为50 s时的仿真曲线，在900 s时加入干扰信号；图4所示是延迟时间τ为200 s时的仿真曲线。图3中PID参数为Kp=0.62，Ti=60，Td=3。图4中PID参数为Kp=0.56，Ti=80，Td=5。仿真结果表明：对于大时滞系统，PID控制超调量大，调节时间长，当τ与T之比大于2.5时会造成系统不稳定。当外加干扰信号时，PID控制算法使系统调整时间长，如图3曲线2所示。TCPA控制算法具有自适应性，超调量小，调节时间较短，过渡过程平稳，在干扰信号作用下控制系统恢复时间短，如图3和图4中曲线1所示。可见：TCPA控制算法对于阶跃信号能在较快的时间内达到稳定状态，动态性能好，控制精度高，鲁棒性强。

2 多重大时滞控制系统数学模型

2.1 多重大时滞系统工作原理和结构框图

设生产工序有n个控制点cp1, …,cpn，生产工艺指标，通过设定值分解器分解矩阵获得各控制点的设定值，它们分别输入 M-TCPA控制器的TCi，控制器分别输出控制量ui(k)，i=1, 2, …,n，通过n个执行机构控制多重大时滞系统被控对象，其控制系统结构框图如图5所示。图5中：工序参数检测环节输出表示工艺指标的参数值，在实际生产过程中，它们往往不能直接在线检测，一般要对产品采样进行离线分析化验得到，这样产生的延迟时间达到几十分钟，甚至几小时，图中用延迟环节表示，D是延迟时间。产品的工艺指标通过输出分解器输出n个输出变量y1(k),y2(k), …,yn(k)，分别反馈到n个控制点实现闭环控制，保证跟踪n个设定值的控制精度。当设定值分解器输出的设定值有偏差，通过工艺指标反馈值与工艺指标设定值的比较形成控制量设定值偏差ΔR(k)，由设定值偏差校正分解矩阵α，输出n个设定值的修正量，分别对n个控制点的设定值进行修正。设定值分解和设定值偏差校正都是按照实际经验、依据工艺参数指标进行的。

2.2 多重大时滞系统数学模型

式中：D1为对角矩阵diag[d11,d12, …,d1n]，根据工艺要求计算得到。例如氧化铝生产连续碳酸化分解过程中，1#槽至6#槽分解率设定值d11,d12, …,d16分别为27.8%，63.4%，87.1%，93.8%，95.8%和 96.5%，形成合适的分解梯度，获得最佳的氧化铝产品质量、尽可能少的能量和CO2消耗量。

设定值向量经过校正后，得到多重时间协调参数自调整控制器(M-TCPA)的给定值：

图5 多重大时滞控制系统结构原理图Fig.5 Principle block diagram of multiple long time delay control system

各个TCPA控制器的输出ui(k)：

令

为对角矩阵，不考虑n个脉冲响应等效系统之间的耦合，得到：

由式(8)得到：

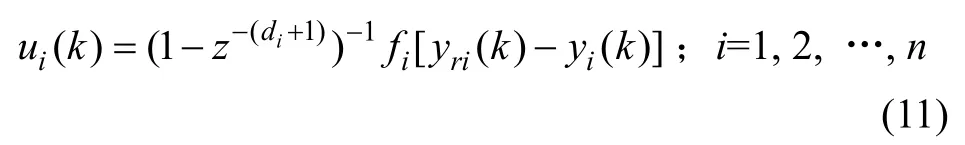
将式(12)代入式(9)经过整理获得多重大时滞系统对设定值的系统响应输出Y(k)表达式为：

改变式(13)中M-TCPA控制器的增益F，可调节闭环系统的极点和零点，来获得闭环控制系统期望的控制精度和动态特性。M-TCPA控制策略应用于某氧化铝生产厂连续碳酸化分解过程，影响碳酸化分解率的主要因素有铝酸钠溶液的流量、CO2通气量以及分解槽液位高低。在碳酸化分解过程中，通过调节铝酸钠溶液的流量和CO2通气量来改变分解率，且每个分解槽应必须保持一定的液位高度，保证CO2吸收率，使整个生产过程连续稳定运行。该控制策略实现了碳酸化分解工序的闭环稳定控制，氧化铝合格率从原来的94.0%上升到95.5%，合格率提高了1.5%。氧化铝合格率实际工艺曲线如图6所示。

图6 氧化铝合格率实际工艺曲线Fig.6 Actual flow curve of alumina qualification rate

3 结论

(1) 长流程生产过程根据生产工艺要求，在工序生产设备不同部位设置了多个控制点，使其不同的控制信号到工序出口处的输出量产生不同的响应延迟。由于传质输送和完成相应的物理化学反应需要较长时间，从而构成了多重大时滞控制系统。使k时刻的输出量y(k)与控制量u(k)产生信息“错位”，会引起闭环控制系统不稳定。

(2) 时间协调参数调整控制策略(TCPA)采用时间协调方法，根据大时滞时间长度τ，形成基本控制量，实现u(k-d-1)与其对应的输出误差的一致性。由输出反馈误差修正控制量，利用内模控制器原理产生自适应性，保证系统控制精度和稳定性。

(3) 给出了一种M-TCPA 多重大时滞控制系统的原理结构框图，利用系统对多控制点设定值的输出响应校正闭环系统脉冲传递函数矩阵中的元素，实现对被控制对象参数变化的自适应性，获得期望的控制精度。调节系统的零极点配置，改善系统的动态性能。

[1] Kaya I. A new Smith predictor and controller for control of process with long dead time[J]. ISA Transactions,2003, 42:101-110.

[2] Kaya I. IMC based automatic tuning method for PID controllers in a Smith predictor configuration[J]. Computers and Chemical Engineering, 2004, 28: 281-290.

[3] 朱晓东, 王军, 万红. 基于Smith预估的纯滞后系统的控制[J].郑州大学学报: 工学版, 2004, 25(1): 77-81.ZHU Xiao-dong, WANG Jun, WAN Hong. The control of time delay system based on Smith predicator[J]. Journal of Zhengzhou University: Engineering Science, 2004, 25(1):77-81.

[4] Giles R F, Bartley T M. Gain-adaptive dead time compensation[J]. ISA Transactions, 1977(1): 46-49.

[5] 鲁照权, 韩江洪. 一种新型增益自适应Smith预估器[J]. 仪器仪表学报, 2002, 23(2): 195-196, 199.LU Zhao-quan, HAN Jiang-hong. A new kind of gain adaptive Smith predictor[J]. Chinese Journal of Scientific Instrument,2002, 23(2): 195-196, 199.

[6] 鲁照权, 韩江洪. 对象参考参数自适应时滞补偿器[J]. 控制与决策, 2001, 16(2): 239-241.LU Zhao-quan, HAN Jiang-hong. Object reference adaptive dead time compensation[J]. Control and Decision, 2001, 16(2):239-241.

[7] 达飞鹏, 宋文忠. 大时滞系统的智能控制研究[J]. 中国电机工程学报, 2003, 23(9): 186-188.DA Fei-peng, SONG Wen-zhong. Intelligent controller design for system of long time delay[J]. Proceedings of the Chinese Society for Electrical Engineering, 2003, 23(9): 186-188.

[8] 沈洁, 刘贺平, 许鸣珠. 一种基于模糊RBF神经网络的Smith预估器[J]. 控制工程, 2007, 41(1): 45-48.SHEN Jie, LIU He-ping, XU Ming-zhu. A Smith predictor based on fuzzy RBF neural network[J]. Control Engineering of China,2007, 41(1): 45-48.

[9] 文定都. 针对纯滞后系统的RBF神经网络智能控制的研究[J].工业仪表与自动化装置, 2008(2): 31-34.WEN Ding-du. Research on the RBF neural network-based intelligent control for improving a control system with time delay[J]. Industrial Instrumentation and Automation, 2008(2):31-34.

[10] Aoki S, Kuwachi S, Sugeno M. Application of fuzzy control logic for dead-time process in a glass melting furnace[J]. Fuzzy Sets and System, 2003, 38(1): 251-265.

[11] 周彦, 何小阳. 时变大滞后过程的专家模糊控制设计与仿真[J]. 系统仿真学报, 2006, 18(10): 2786-2789.ZHOU Yan, HE Xiao-yang. Design and simulation of expert fuzzy control for time-varying processes with large time delay[J].Journal of System Simulation, 2006, 18(10): 2786-2789.

[12] 史旭华. 带积分的模糊 Smith预估器在电加热温度控制中的应用[J]. 工业仪表与自动化装置, 2004(2): 33-35.SHI Xu-hua. The application of an integrated fuzzy Smith predictor to the temperature control of an electric oven[J].Industrial Instrumentation and Automation, 2004(2): 33-35.

[13] XU Sheng-yuan, Lam J. New results on delay-dependent robustH∞control for systems with time-varying delay[J]. Automatic,2006, 42: 343-348.

[14] 桂卫华, 刘碧玉. 一类不确定时滞关联非线性系统分散鲁棒H∞控制[J]. 中南大学学报: 自然科学报, 2005, 36(5):846-851.GUI Wei-hua, LIU Bi-yu. Decentralized robustH∞control for a class of uncertain interconnected nonlinear systems with time delays[J]. Journal of Central South University: Science and Technology, 2005, 36(5): 846-851.

[15] 吴敏, 张先明, 佘锦华. 线性时滞系统的时滞相关鲁棒控制[J]. 控制理论与应用, 2005, 22(4): 619-622.WU Min, ZHANG Xian-ming, SHE Jin-hua. Delay-dependent robust control for linear time-delay uncertain systems[J]. Control Theory and Applications, 2005, 22(4): 619-622.