颗粒组分特性对扬矿硬管输送速度的影响

周知进，刘爱军，夏毅敏，唐达生

(1. 湖南科技大学 机电工程学院，湖南 湘潭，411201；2. 中南大学 机电工程学院，湖南 长沙，410083；3. 长沙矿冶研究院 深海矿产资源开发利用技术国家重点实验室，湖南 长沙，410012)

海底矿产资源锰结核主要赋存于水深3～5 km的海底沉积物表层，以全埋或半埋形式镶嵌在海底沉积物中。由于锰结核储存量非常巨大[1]，因而，正成为许多国家研究与开发的热点领域。但是，深海锰结核开采是一个高新技术密集以及多学科交叉的研究领域，其开采系统更是一个庞大复杂的系统工程，集矿和扬矿2个子系统是深海矿产资源开发装置中的核心部分。为了开发这种多金属锰结核矿产资源，国内外已开发出十几种可能的采矿试验系统和设计方案，其中最具有实用价值与应用前途的是水力提升采矿系统，它由集矿子系统、扬矿子系统、遥测遥控子系统和海面支持子系统等组成。水力提升采矿系统的工艺过程为：利用自行式集矿机将赋存于海底沉积物中的锰结核采集起来，经过脱泥、破碎后，由软管输送到离海底200 m左右的中继料仓，然后，通过给料机将结核泵入提升主管道，再由矿浆泵将结核输送到海面采矿船上[2]。根据目前设计的采矿系统，提升锰结核最佳直径在5～50 mm之间。为了获得锰结核的最优的输送速度，降低能耗，有必要研究影响锰结核输送速度的因素。因为锰结核输送速度是水力管道输送的 1个非常重要参数，不仅影响非均质流的浓度分布，而且也影响非均质流速度分布和管道摩阻损失。在固体物料管道水力输送方面，Xing等[3-7]进行了卓有成效的研究工作。1944年美国建成了第1条长24 km的输煤管道。到20世纪90年代末，美国、波兰、加拿大等国已建成固体输送管道系统，输送的固体颗粒主要有煤炭、铁矿石、矿渣等平均粒径为0.03～0.08 mm的颗粒，一般管道呈水平或小于 14°倾斜角布置。这方面的理论和技术都比较成熟，但对粗颗粒垂直远距离水力输送参数优化的理论与技术的研究较少，还远没有到达实际应用的程度，大部分还处于实验室研究阶段。为了将锰结核矿石从中间仓提升到海面采矿船上，最小输送速度是扬矿系统设计中需要考虑的1个重要参数[4]。因为若输送水流速度过高，不但使管道内壁磨损加剧，阻力增加，而且也会消耗更多的能量；若水流过小，则固体颗粒输送不上来。所以，最小输送速度既要保证固体颗粒持续输送上来，不会造成堵管的危险，又不会造成管道磨损加剧与能量消耗过大。

1 固体颗粒在垂直管道中的运动规律

当不同固体颗粒在密度存在差异的流体中运动时，颗粒表面形状不可能像流体质点那样对周围压力及时做出反应。这种差异的存在使得颗粒运动速度比输送流体速度慢，两者之间速度差称为滑移速度。由于滑移速度的存在造成固体颗粒在管内滞留，从而使当地浓度大于输送浓度(也称出口浓度)。若是输送速度较低时，管道当地浓度就会增加，当达到一定程度时，就会造成堵管。

单个固体颗粒在圆管中随水流作上升运动时。作用在固体颗粒上的力有重力FG、浮力Ff、阻力Fz、附加质量力Fa以及Magnus力。

固体颗粒开始下沉时，颗粒速度vs相对较小，重力大于阻力与浮力之和，颗粒加速下降。随着颗粒速度的加大，水的阻力以相对速度呈2次方增长，经过一定距离后，重力、浮力与阻力相等，固体颗粒以匀速运动下降，这时附加质量力和 Magnus力可以忽略不计，固体颗粒的匀速运动就是其在静水中的沉降速度。沉降过程用公式表示为：

但是，锰结核形状复杂，且个体差异较大，形状极其不规则。所以，当形状不规则的固体颗粒沉降时，其所受到的沉降阻力要比同体积的球形固体颗粒所受到的沉降阻力大。固体颗粒的形状越不规则，其所受的沉降阻力就越大。Swanson的形状系数α和β就是反映固体颗粒形状对沉降速度影响的具体参数，其取值直接与固体颗粒沉降时其周围的流体流动有关。具体表达式为[2]：

式中：μ为水的黏性系数；ki为固体颗粒的面积指数，；b和c分别为椭圆形颗粒截面的长半径和短半径；de为等容直径，按不规则形状计算等容粒径，这里采用del计算面积指数。

固体颗粒的沉积速度由于颗粒密度、形状、直径等不同而不同，一般通过静水中沉积试验获得沉积速度，通过沉积速度计算阻力系数CD，利用这个阻力系数通过一些修正公式可以计算沉积速度。当颗粒在上升流中处于悬浮状态时，水流对颗粒的升力与颗粒的在水中有效重力相等，此时，水流速度就是颗粒的沉降速度。若进一步提高水流输送速度，固体颗粒将随水流一起运动，但颗粒的运动速度小于输送速度，从而造成管道出口浓度小于管中当地浓度，若两者相差较大时，则会引起管道堵塞。

当地浓度与输送浓度的转换关系通过固相与液相的质量平衡推导出来[5]：设流体速度为vq，两相流平均速度为vm，颗粒群滑移速度为vr，管道横截面积为A。根据管道内、管道出口固体颗粒流量相等，可得：

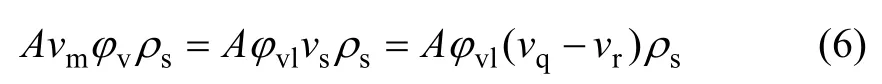
同样，按管道任意一处流量与出口流量相等，可得：

由式(1)和式(2)联立，可以求出φvl[7]：

由式(8)可以看出：管内浓度与输送速度、输送浓度及颗粒群滑移速度有关。输送速度越小，滑移现象就越显著，颗粒在管内滞留的效应就越明显[8]。当在输送速度和输送浓度确定的情况下，颗粒群的滑移速度是影响管内当地浓度的关键因素。因此。一旦颗粒群的滑移速度被确定，当地浓度就可以计算出来。但是，确定颗粒群精确的滑移速度是相当困难的，这是因为颗粒越粗大，颗粒终端速度和固液滑移速度就越大，颗粒在两相流中的流动速度就越小，所以，颗粒群中单个颗粒的流动速度是不相同的，其滑移速度也随颗粒特性不同而有差别[9-10]，为此，研究粗颗粒输送过程中颗粒级配参数对水流输送速度的影响，从而确定耗能较少级配较优的特征参数，进而确定临界输送速度。

式中：C为常数，由粗颗粒物料级配特征参数和极限体积分数来确定。

2 试验结果与计算值对比分析

根据前面的理论分析，单个颗粒的滑移速度可以通过试验手段得出，其最大滑移速度就是其沉降速度。随着输送水流速度的增大，颗粒运动速度与输送流体速度之间差距越来越小，但即使输送速度趋于+∞，滑移速度仍然存在。

利用长沙矿冶研究院海洋所扬矿组的试验结果进行分析[11]。他们采用未经过破碎的天然锰结核颗粒进行沉降试验。试验在高为3 m、直径为500 mm的圆柱形有机玻璃水槽中进行，有效测量高度为 2 100 mm，试验沉降速度结果是多次实验的平均值。单个颗粒沉降速度的试验结果与计算结果如表1所示。

从表1可以得出：通过式(2)计算出的颗粒沉降速度与实验结果相差非常大，这是阻力系数CD取值不同以及锰结核形状极其不规则所致。为此，引入2个表征形状系数的参数α和β，对沉降速度公式进行修正，其计算结果见表1中的vt，它与试验结果之间的误差如图1所示。从图1可见：颗粒也接近球形，试验结果与计算结果吻合越好；颗粒越不规则，两者之间误差就越大[12]。

前面进行的单个颗粒的沉降速度实验与计算是为了研究问题的简化。而在实际管道输送应用中，颗粒以群体形式在管道中运动，既存在固相与液相之间的相互作用，也存在同相之间的相互作用。由于颗粒群是由不同级配的颗粒组成的，不同粒径在相同流体速度作用下又具有不同的滑移速度，因而，级配特征参数是管道输送中必须考虑的关键因素[13-14]。

当整个固液两相流输送达到稳定后，分别对不同取样点颗粒浓度进行测量，并根据不同的颗粒级配和输送速度，确定颗粒数量浓度在提升管道内分布规律及变化情况。采用海洋4号和大洋1号所采集的天然锰结核经过齿辊式破碎机破碎后颗粒筛分的结果，如表2所示[9]。

表1 单个锰结核颗粒在静水中沉降速度理论结果与计算结果Table 1 Settling velocity theoretical data and calculation results of single manganese nodule particle in static water

不同粒径区间的颗粒直径分别为36.0，28.5，20.0，12.5，7.5和2.5 mm，级配按表3所示的质量分数分配。假定不同粒径所占质量分数在上述2种情况下之间波动。

利用RSM模型优势，即RSM是一种有效的统计技术，它是利用实验数据，通过建立数学模型来解决受多种因素影响的最优组合问题。对RSM的研究表明：研究工作和研究目标可以在更广泛的范围内考虑因素的组合以及对响应值的预测。现在利用采用FLUENT软件包可以方便地对响应面进行分析。对管道内固液两相流场进行模拟分析后，得出在不同级配曲线上颗粒体积分数与输送速度的关系如图2所示。

图1 单个颗粒沉降速度试验值与计算值之间的对比曲线Fig.1 Comparison curves of settling velocity experimental data and calculation results of single manganese nodule particle

表2 天然锰结核破碎后的试验结果Table 2 Experimental results of natural manganese nodule

表3 颗粒直径不同时级配分布(质量分数)Table 3 Distribution of original scale of various diameter particles %

图2 颗粒输送速度随体积分数变化曲线Fig.2 Change curves of transportation speed with volume concentration

从图2可以看出：对于同一级配下输送速度随着体积分数的增大而增大。这主要是颗粒体积分数增大以后，颗粒之间的碰撞概率增大，导致输送速度也随之增加；当体积分数达到20%以后，输送速度的增长率有所减小，说明输送颗粒在管道内分布趋于均匀，颗粒之间碰撞概率也相应减小。但体积分数达到一定值以后，由于颗粒直径范围较大，不同粒径的颗粒之间滑移速度愈加明显，从而造成不同粒径的颗粒之间碰撞概率又有所增加，体积分数与输送速度又呈现增长趋势。对于不同级配情况，与输送速度处于最优匹配的颗粒体积分数为20%～25%。当大颗粒在级配中占优势时，所需的输送速度增大较快。

3 结论

(1) 单个颗粒在垂直水流中的最小临界速度就是其沉降速度，当水流速度继续增大超过沉降速度后，滑移速度逐渐减小。无论水流速度如何变化，颗粒直径越大，滑移速度也越大。

(2) 在同一级配下，输送速度随着颗粒体积分数的增大而增大，当达到某一值后，增长速度减小。随着颗粒体积分数进一步加大，输送速度又随着颗粒体积分数增加。

(3) 在不同级配情况下，粗颗粒体积分数较大时，颗粒体积分数超过某一值后，输送速度随颗粒体积分数增长速度比中细颗粒体积分数较大的输送增长速度快。

[1] Rolinski S. Dispersion assessment of particulate substances from deep-sea mining activities by means of model simulations[J].German Journal of Hydrography, 1999, 10(Supplement):141-146.

[2] 田龙, 李鹏程, 姜龙, 等. 垂直管固体物料水力输送浓度的研究[J]. 泥沙研究, 2006(2): 72-76.TIAN Long, LI Peng-cheng, JIANG Long, et al. Study on concentration of large size particles in vertical pipes by hydraulic lifting[J]. Journal of Sediment Research, 2006(2): 72-76.

[3] XIANG Jian-sheng, McGlinchey D. Numerical simulation of particle motion in dense phase Pneumatic conveying[J]. Granular Matter, 2004(6): 167-172.

[4] Konrad K. Dense-phase pneumatic conveying: A review[J].Powder Technology, 1986, 49: 1-35.

[5] Tsuji Y, Kawaguchi T, Tanaka T. Discrete particle simulation of two-dimensional fluidized bed[J]. Powder Technology,1993, 77:79-87.

[6] 孙恒虎, 段鸿杰, 刘华生. 应用确定有效细粒群的最佳配比[J]. 北京科技大学学报, 2003, 25(6): 504-506.SUN Heng-hu, DUAN Hong-jie, LIU Hua-sheng. Application ofto optimum ratio determination of effective silt particles[J]. Journal of University of Science and Technology Beijing, 2003, 25(6): 504-506.

[7] Tsuji Y. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J]. Powder Technology, 1992, 71: 239-250.

[8] Greimann B P. Two-phase flow analysis of sediment velocity[C]//Proceedings of the Sedimentation and Sediment Transport.Lush, Switzerland, 2002: 83-86.

[9] ZHAO Zhi-he, Fernando H J S. Numerical simulation of scour around pipelines using an Euler–Euler coupled two-phase model[J]. Environ Fluid Mech, 2007, 7: 121-142.

[10] Liang D, Cheng L, Li F. Numerical modeling flow and scour below a pipeline in currents. Part Ⅱ: Scour simulation[J].Coastal Eng, 2005, 52: 43-62.

[11] XIA Jian-xin, NI Jin-ren, Mendoza C. Upward flow of large size particles-water mixtures through swaying pipe[J]. Journal of Transportation Engineering, ASCE, 2004, 130 (4): 535-543.

[12] Amoudry L O, Liu P L F. Two-dimensional, two-phase granular sediment transport model with applications to scouring downstream of an apron[J]. Coastal Eng, 2009, 56(7): 693-702.

[13] Brown P P, Lawler D F. Sphere drag and settling velocity revisited[J]. Journal of Environmental Engineering, ASCE, 2003,129(3): 222-231.

[14] Dai X, Boll J. Settling velocity of cryptosporidium parvum and Giardia lamblia[J]. Water Research, 2006, 40: 1321-1325.