“多元”关联模式的时空数据挖掘

陈新保 ，LI Song-nian，朱建军，陈建群

(1.中南大学 地球科学与信息物理学院，湖南 长沙，410083；2. 瑞尔森大学 土木工程系，加拿大 多伦多，M5B 2K3)

空间数据关联挖掘为基于空间关联的知识获取提供了途径，在交通[1]、生物[2-3]、公共安全[4]、气候[5]、人口普查[6]等领域有广泛的用途。经过数十年的发展，国内外对空间数据关联模式挖掘的研究[2,7-14]已取得一些成果。对空间关联挖掘的研究主要体现在两大方面：一方面，基于数值型的地理要素的区域(Region)关联规则挖掘，即地理要素的“点”、“线”和“面”状数值转化为定性“级别”或“布尔型”，对其在参考区域内的“交易频繁”分析，适合基于位置的空间数据类型，如栅格数据[15]或属性值的地理要素。Mennis等[9]用关联分析法，很好地诠释了社会地理要素(社会经济指标)与自然地理要素(土地覆盖值)的因果机制；但在关联分析中，局限于“面域”空间维的关联挖掘。Lee等[4,16]提出了“点”、“线”和“面”等空间多维的关联挖掘分析，但他们都将“点”和“线”特性值转化为“面域”值，仍然是在“面域”的基础上进行分析。同样，Ding等[17]提出了基于“面域”关联挖掘的框架，并引入“面域”关联规则的空间影响度(Scoping)。另一方面，基于离散型对象在整个空间数据集中的“交易”分析，此时“交易”的对象可以是空间对象本身，也可对象间的关系。Yang等[10,18]基于空间对象的距离关系探讨了“星型(star)”、“序列型(sequence)”和“晶体型(clique)”等关联模式。Lee等[19]则对“trajectory”关联模式进行了探讨。不过，这些组合式关联规则在空间对象和关系上都较单一，属于同类和同质。Huang等[20]已经扩展到复杂空间对象(例如线和多边形异类)，但都最终当作“面点”对象来挖掘。对于挖掘算法，Agrawal等[21]首先提出关联规则模型，并给出求解算法AIS来挖掘顾客交易数据库中项集间的关联规则问题。此后，诸多研究人员对关联规则的挖掘算法进行了研究，出现了SETM和Apriori等算法。其中，Apriori已经成为关联规则模型中的经典算法，许多相关研究[12,22-25]对该算法进行了改进，其核心是基于两阶段频集思想的递推算法，即用频繁的(k–1)项集生成候选的频繁k-项集和用数据库扫描和模式匹配计算候选集的支持度和置信度；Apriori算法要求关联规则在分类上属于单维、单层、布尔关联规则。但是，上述空间关联模式和挖掘算法存在以下问题：一是挖掘源主要集中于空间数据库，而缺乏考虑时间或淡化时间在整个挖掘过程的存在；二是空间关联维度局限于单维，如(X→Y)规则，要求X和Y为同类型要素，即点对点、线对线和面对面等；空间关联规则构建较单一：要求同质，如X→Y规则可能局限于空间拓扑规则，对混合的空间关联规则研究较少；三为挖掘算法针对单规则，不适合多规则组合式模式。由此，本文作者对空间关联模式挖掘进行了进一步工作：(1) 挖掘源从空间数据库扩展到时空数据库，挖掘的对象也从空间数据扩展到时空数据，即从大量历史地理空间要素中挖掘某种时空关联模式；(2) 空间关联规则以空间关系和时态关系为主，空间关联的对象扩展至地理要素，即要素“多类型”和关联“多规则”；(3) 用图论构建和表达如“星型”和“序列型”等多类型要素下的多规则的关联组合模式，即“多元”关联模式；(4) 探讨“多元”关联模式下的挖掘算法。

1 问题描述

空间对象关联模式类型如图1所示。与传统空间关联组合模式不同，“多元”关联模式呈现以下特性：(1) 挖掘对象扩展至地理要素，可处理复杂的空间对象(如线和面等概化的地理要素)；(2) 地理要素间的多种空间关系(如距离、方向和拓扑等)同时存在；(3) 要素间存在着时态关系；(4) 要素间可能存在某地理经济要素(如GDP)跟地理基础要素的约束关系。此时，模式存在“多类型”和“多关系”下的多个要素共同参与的关联组合，将此类组合统称为“多元”关联模式。而对此类模式的挖掘和发现称之为“多元”关联模式的时空数据挖掘。在此特说明，本文所涉及的挖掘关联要素多源于有限的离散要素集。显然，“多元”的概念可概括为：要素有多个且呈现类型多样性(即“多类型”)以及要素间关系异质多样性(即“多规则”)。现就“多元”关联模式构建与挖掘中一些基本概念和问题表述给予定义和形式化阐述。

定义 1 地理要素。地理要素(Geographic feature,GF)是指地理空间中具有确定的位置和形态特征的有地理意义的实体，它是现实世界的地理实体在计算机中的表达。根据要素特征不同，地理要素可分成多种类型(FeatureType)，如点、线、面和实体等几何要素。依据要素的功能不同，地理要素亦可分成多种类型，如城市规划中的道路(Road)、房屋等，而道路又细分成高速路、铁路等；房屋可划分为居住和商业等。设F={f1,f2, …,fr}为地理要素类别集合。

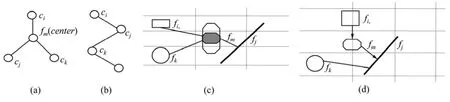
图1 空间对象关联模式类型Fig.1 Type of association patterns

规定1 设时空数据库D={＜obj1,obj2，…＞,…,objN}，则地理对象集＜obj1,obj2，…,objm＞∈fi为地理要素类别fi的m个具体实例(Instance)或记录(Record)，每个实例的属性集可表示为＜Instance Id,FeatureType,fId＞。fId为fi所属要素类型的标识符；实例具有时态性，其时间属性描述为＜sTime,duration＞，即sTime为起始时间(ts)，duration为存在持续时间td。

定义 2 要素关联规则。要素关联规则(Feature association rule, FAR)是反映地理要素间关系(或结构)一些显性特征，是区域地理要素在空间和时间上的组合方式的最基本描述。关注空间数据，强调要素在时间和空间上的位置布局，则时间、方向、距离和拓扑是要素关联规则描述、表达与获取的最基本规则。

规定2 设要素关联规则函数RL，它对每个命题逻辑语义La中的要素fi，fj赋以实体RL(Fp)，则有：

其中：isTemp指要素fi和fj间的时态关系；isDist指要素fi和fj间的距离关系；isOrien指要素fi和fj间的方位关系；isTopo指要素fi和fj间的拓扑关系。可以用wij=RL(fi,fj) 表征RL(fi,fj)规则集函数，例如横穿某城市的干道fi于2000年顺利通车，其后某二环线fj于2005年竣工，两者存在空间相交和时间先后关系，于是，可表达成：wij=RL(fi,fj)={before,far-away,NO,intersect}或所对应的索引标识符[13]形式{101, 200, 300, 415}。

4种关联关系具体描述如下。

(1) 时态关系，如时间先后等；时态谓词描述：isTemp(operator1)。其中：operator1为时态算子，如before(前)/after(后)/equal(相等)/start(起始)/meet(相接)/overlap(相叠)等。

(2) 空间定向，即 GIS方位谓词描述：isOrien(operator2)，其中，operator2为方位算子，如east-of(东)/west-of(西)/south-of(南)/north-of(北)等。

(3) 空间距离，距离谓词描述为isDist(operator3)。其中：operator3为距离算子，如DisConstant(距离常数)、CloseTo(接近关系)和Far-away(远离关系)。以及定量表示距离的算子distance；若distance(x, y)≤DisConstant，则x，y的距离关系为CloseTo，否则，为Far-away。

(4) 拓扑关系，即 GIS拓扑谓词描述：isTopo(operator4)，其中，operator4 为拓扑算子，如disjoint(相隔)/intersect(相交)/contain(包含)等。

定义 3 “多元”关联模式挖掘。“多元”关联模式容许多类型的地理要素和多异质的关联规则同时存在，那么挖掘“多元”关联模式挖掘的过程就是对多种规则组合式的发现。本文只涉及时空数据关联挖掘，其时空数据源于有限的离散地理要素集。此时，时空关联挖掘过程的形式化定义为：

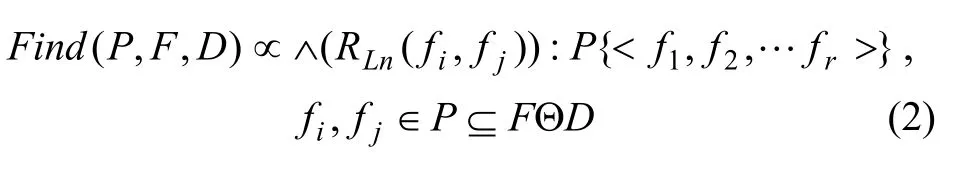
式中：Find(P,F,D)就是对n个“显著”RL关联规则(n≥2)的关联组合，从而形成关联规则P模式。

规定 3 与传统关联规则挖掘一样，将“支持度(Support)”和“置信度(Confidence)”确定为衡量一个要素关联规则重要性的2个关键性指标。在关联规则挖掘中，由于地理要素缺乏“交易”概念，在此用要素间存在某种时空“关系”来表征一种“交易”，其在时空数据库中的多次出现来表达“频繁(Frequency)”特性。设F={f1,f2, …,fr}为r个地理要素类别集，每个类别集都包含数量不等的地理对象；R={r1,r2, …,rn}为n个要素关联关系。则类型不同的2个要素间(X→Y)的某种关联规则表达及其“支持度(sup)”和“置信度(conf)”计算如下：

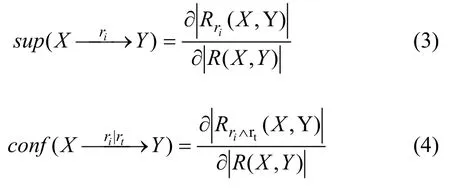
其中：∂为“关系”数量算子。式(3)求解支持度表征着某空间或时间关系的热度；式(4)求解表达某空间关系在某时态关系上的强度。要素关系关联规则X→Y(S，%，C，%)，存在支持度(S，%)和置信度(C，%)。表1所示为支持度和置信度的计算过程。

规定4 关联规则等同性、层次性和显著差异性。关联规则中的拓扑、方位和距离等关系同时存在，且这些关系都置于时态中。它们的重要性在本质上是等同的。但这些关联关系存在层次性：空间关系和时态关系为关联规则同一最高级别；根据空间距离由远及近等，距离级别大于拓扑；而距离和方位层次等同。在求解“显著”性，父层级的关系级数为子层级之和。在挖掘算法中，将“关系”表征为“交易”，用每种“关系”所出现的次数表征着该“关系”的“频繁”。此时，该“频繁”可能呈现“显著差异性”，而高“频繁”表示该“关系”显著。这种“显著”特性对关联模式的挖掘非常重要，影响着拓扑、方向、距离等关系的取舍。某类空间关系“频繁”跟时态关系“频繁”相组合，容易形成某类时空关联模式。如方位且距离关系“显著”(即均衡的位置布局和要素间邻近)和时态“显著”(即关系在某时间段的大量涌现，这种现象称之为“时态聚集”)易形成“星型”模式。空间拓扑的邻近关系(此时表现为高“频繁”)在时间上的先后出现(又表现着高“频繁”)易形成“序列”模式。某两类型地理要素的关联规则“显著”求解步骤：

表1 两要素X→Y“关系”关联规则的“支持度”和“置信度”求解过程Table 1 Calculations of support and confidence degree for FAR of ‘X→Y ’

(3) ifri⊗rt, “显著”, thenRL(ri⊕rt)=“显著”；otherwise“不清楚”。

2 “星型”和“序列型”关联模式搭建

“多元”关联模式挖掘，关联模式的搭建是关键。本文只讨论2种常见的关联模式，分别为“星型”和“序列型”，图1(c)和(d)所示分别为这2种模式在“空间对象关联”和“地理要素‘多元’关联”所不同的表达方式。在“多元”关联模式中，要素间的关系可以表征成有向图(即图论)：节点(Node)对应于要素类型fi∈F；边(Edge)表示节点(要素间)的关联性；边(Edge)的粗细表示节点(要素间)的关联热度强弱；箭头(Arrow)可表征要素间的时态关系，如fi→fj表示fi先于fj；虚线方格(Grid)用于确定要素的空间方位(如东、西、左、右等)。额外，图1(c)所示节点(Node)的多层包围圈，表示不同时间段的要素状态(如形状、大小等)，用颜色填充来标注要素不同的产生时间等。

2.1 星型(Star-like MVAP)

此类模式为要素关联规则模式的一个特例，也是现实中较常见的一种现象：要求有1个“核心”要素，与其他要素间至少存在某种关联关系，其他的要素间不一定要求关联。在此，其他要素可称之为“配套要素”。“星型”模式可描述为P＜fc:{f1, …,fk}＞，且时间顺序有fc＜fl，fc＜f2，…，fc＜fk或fc＞fl，fc＞f2，…，fc＞fk。“星型”模式具体详细说明如图2所示。

(1)a,b,c,g为时空要素的实例，则该“星型”模式的实例可表示为：＜g:{a,b,c}＞；左图要素颜色填充不同，表示要素出现的时间先后顺序不同。

(2) 按要素出现的先后顺序有2种形式：一是“核心”要素出现后，导致其他要素出现，即时间约束为(g.ts＜a.ts)∧(g.ts＜b.ts)∧(g.ts＜c.ts)；二是相关要素相继出现后，“核心”要素才出现，即时间约束为(g.ts＞a.ts)∧(g.ts＞b.ts)∧(g.ts＞c.ts)。

(3) “核心”要素和“配套要素”存在一定的空间关系(如距离和拓扑等)。

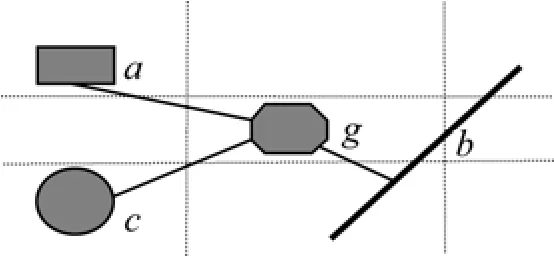
图2 “星型”模式实例Fig.2 An example of ‘start-like’ pattern

2.2 序列型(Sequence MVAP)

此类模式为时空序列模式(Flow patterns)的典型实例，要素个数为k的序列模式可表达为P=要求要素两两间至少存在时间和空间相邻的 2种关联关系。“序列”模式可描述为P＜f1,f2,…,fk＞。“序列型”模式具体说明如图3所示(其中，fj为线要素(如公路))。

(1)a,b,c,d为时空要素的实例，该“序列”模式的实例可表示为：＜a,b,c,d＞；要素颜色填充不同，表示要素出现先后顺序不同。

(2) 空间距离要求“邻近”，拓扑关系要求“相离”：CloseTo(fi,,fi+1)∧Disjoint(fi,,fi+1)。

(3) 时态要求相近，保持时间前后关系，如,fi+1在fi后出现：after(fi,,fi+1)。

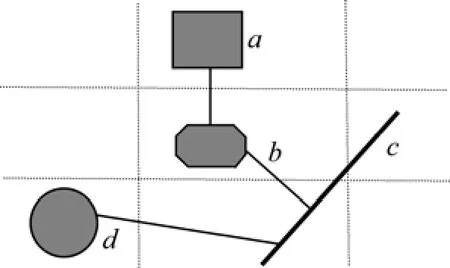
图3 “序列”模式实例Fig.3 An example of ‘sequence-like’ pattern

3 挖掘算法

对“星型”和“序列型”的关联模式进行时空数据挖掘算法探讨。在现有空间关联挖掘Apriori算法的基础上，由单独的同类双要素挖掘扩展至多类型下的多个要素的多规则组合式的模式挖掘。为了方便快速搭建“多元”组合关联模式，引入“等价类”[26]。

3.1 “等价类”概念

定义4 等价类[10,18](Equivalence classes)。

设fi和fj为2个集合，且pk=(fi,fj)为频繁k-MVAP，若fi为(k-1)-MVAPs模式，则称pk为k阶等价类，记为Ek(fi, fj)。其中：Ek为k-等价类集；Ekfi和Ekfj分别为Ek的前缀和后缀要素，且Ek(fi,*)为前缀相同的k-等价类集,Ek(*,fj)为后缀相同的k-等价类集。若Ek的前缀fi或后缀fj要素一致的等价类有m个，则所对应的m个k-MVAPs模式可合并成(k+m-1)-MVAPs模式。

等价类的引入一方面可利用来自同一等价类中的要素项集，快速搭建“多元”时空关联模式，另一方面可降低频集和规则的冗余度，大大提高挖掘的质量。k阶等价类规定须满足2个特性：(1) 其为k阶时空关联模式，记为k-MVAPs；(2) 其前k-1要素集必为k-1阶时空关联模式，记为(k-1)-MVAPs。

3.2 挖掘算法实现

(1) 扫描时空数据库 1次，计算各种专题要素个数N(Fi)，可能时空数据量∑N(Fi)非常大，可根据自身感兴趣的要素或要素级别，即设置要素权重w(Fi)；先检索，后扫描，去除不重要或意义不大的要素，生成一新的表。若w(Fi)×N(Fi)/∑N(Fi)≥wminSup(权重支持度)，则p1i(Fi)为1-MVAP频繁模式，P1={p11,p12, …,p1i}为一阶频繁集。

(2) 依照时空谓词算子和时空关系层次化的搜索原则，先时态算子(operator1)、方位算子(operator2)、距离算子(operator3)和拓扑算子(operator4)，对一阶频繁集(P1)进行扫描，并记录该算子下的关系次数；若两要素p2i(fi,fj)满足以下情况：(1) 在时间上满足|fit-fjt|≤t，空间距离满足distance(fj-fi)≤d，且 N(p1i)/ ∑N(p1i)≥minSup，则p2i(fi,fj)为2-MVAPs“准星型”频繁模式，P2={p21,p22, …,p2i}为“准星型”二阶频繁集；(2) 在时间上满足fjt-fit≤t(i＜j且t＞0)，空间距离满足distance(fj-fi)≤d，且N(p1i)/∑N(p1i)≥minSup，则p2i(fi,fj)为2-MVAPs“准序列”频繁模式，P2={p21,p22,…,p2i}为“准序列”二阶频繁集。

(3) 在二阶频繁集(P2)的基础上，构建2-等价类，即两要素p2i(fi,fj)为频繁2-MVAPs模式，且fi,fi∈P1，则p2i(fi,fj)也为 2-等价类，记为E2(fi,fj)。其中：E2为2-等价类集，E2.fi,E2.fj分别为E2的前缀和后缀要素，又且E2(fi,*)为前缀相同的为2-等价类集，E2(*,fj)为后缀相同的为2-等价类集。例如：p21=(f1,f2)(其中，f1为1-MVAP频繁模式)，则p21为2-等价类，记为E2(f1,f2)，即E2(f1,*)为前缀相同的为2-等价类集。

(4) 在2-等价类集(E2)中，搜索相关等价类，分别搭建所需要的多元关联模式，若E2的前缀fi或后缀fj要素一致的等价类有m个，则所对应的m个2-MVAP模式可合并构建成(m+1)-MVAP“星型”模式；若E2的后缀fj要素和前缀fi相同，且有m个这样的等价类，则所对应的m个 2-MVAP模式可合并构建成(m+1)-MVAP“序列型”模式。又如：

对于“星型”关联模，

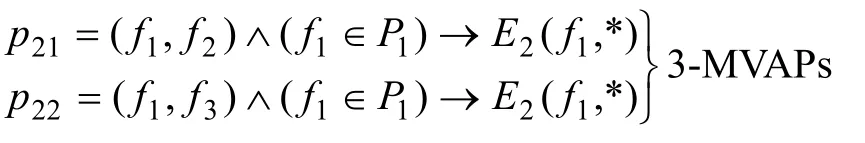
对于“序列”关联模，

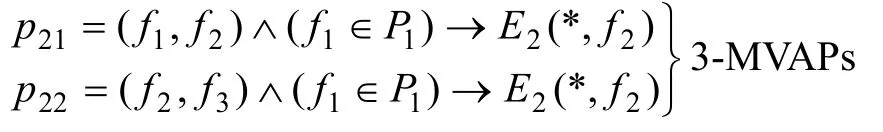
具体算法实现如下：

//Algorithm算法: MVAPs-Mining

//目的: 从时空数据源中，挖掘出类似“星型”和“序列”的时空关联模式

Input: Spatiotemporal DatabaseD;

Spatial Distance thresholdR;

Time spanning thresholdW;

Minimum Support minSup;

Output: A set of frequent “Start-like” St;

A set of frequent “Sequence” Se;

1.Scan databaseDand classified into n thematic layers,formedFi (if necessary);

2.P1←Gen1-MVAPs(minSup); //Generalize 1-MVAPs;

3.Θ(fi∈D)∩(P1≠Φ)

4. FOR Each featurefi∈P1ANDi＜∑N(Fi)DO

5.i+=1; // GenRelation-ST(fi,fi+1,R,W,Type): The Solving process of Spatiotemporal relationships

6.St_P2i←GenRelation-ST(fi,fi+1,R,W,St); //Generalize Candidate with “Star-like” pattern;

7.Se_P2i←GenRelation-ST(fi,fi+1,R,W,Se); //Generalize Candidate 2-MVAPs with “Sequence” pattern;

8.St_P2←St_P2i;Se_P2←Se_P2i;P2←{St_P2,Se_P2}; //2-MVAPs

9.END FOR

10.FOR Each relationshipsRj∈P2ANDj＜iDO

11. IF(Rj.fleft∈P1)and (Rj.fright∈P1)THEN //construct the Equivalence classes

12.k+=1;E2(k)={Rj.fleft,Rj.fright};E2←E2(k); //E2sets

13. END IF

14.END FOR

15. FOR Each classE2(m)∈E2ANDm＜kDO //fix up those“star-like” and “sequence” patterns

16.n=p=q=0; St_temp(0)= Se_temp(0)=E2(m);

17. FORn＜k-mDO

17.n+=1;

18. IF (E2(m).fleft)=(E2(m+n).fleft) THEN //the “star- like”pattern

19. St_temp (p+1)←{E2(m+n).fright};END IF

20. IF (E2(m).fright)=(E2(m+n).fleft) THEN //the “sequence”pattern

21.Se_temp(q)=E2(m); Se_temp(q+1)←{Se_temp(q)}∪{E2(m+n).fright}; END IF

22. END FOR

23.St←St_temp(p);Se←Se_temp(q);

24. END FOR

4 合成实例求证-城市规划

城市化是构建在社会经济发展过程中的时空演变过程。城市化空间格局与城市化空间过程是揭示城市化进程的2个重要方面[13]。而对城市空间规划诸方法的研究中，尤其是发现城市各空间要素间的秩序与逻辑的方法和技术，历来都是城市规划研究的热点和前沿性课题。而对时空关联模式的研究有助于释义城市空间的位置和结构布局模式以及揭示城市化过程的演变，进而深入解析城市各地理要素的空间效用和功能[27]。城市化进程中的要素符合“有限的离散的地理要素集”特性，特用合成实例(城市规划)诠释“多元”关联模式的时空数据挖掘过程，验证模式及其挖掘算法的可用性。在此，更重视模式从规划时空数据集的构建到模式挖掘的整个过程，而忽略挖掘算法的效率等问题。

4.1 规划要素集

现实的地理规划要素需在计算机中得以表达，才能实现数据的存储，故首先需要构建数据集。规划要素具有时间和空间属性，以(空间)数据库方式存储，进而形成所谓的时空地理要素集即规划要素时空数据集，用符号D表示，时空数据集具有时空特性。设时空数据集D共有n个地理要素fi，各自分布在r个数据集中。若数据集对应于时间快照(Snapshot)图，则快照图可表示成:W={W1,W2,…,Wr}。其中：Wi是按时间排序：W1＜W2＜…＜Wr；若数据集对应于专题(Thematic maps)图，则专题图可表示成：M={m1,m2,…,mr}(其中，mi可按数据类型划分：m1|m2|…|mm，可做多维度时空关联挖掘)；如两者都存在，则考虑先按要素类型分类，再按时间排序。假设n个要素存在q种 MVAPs，则模式集对应于P={p1,p2,…,pq}。时空数据集的记录和存储方式，如图4和表2所示。

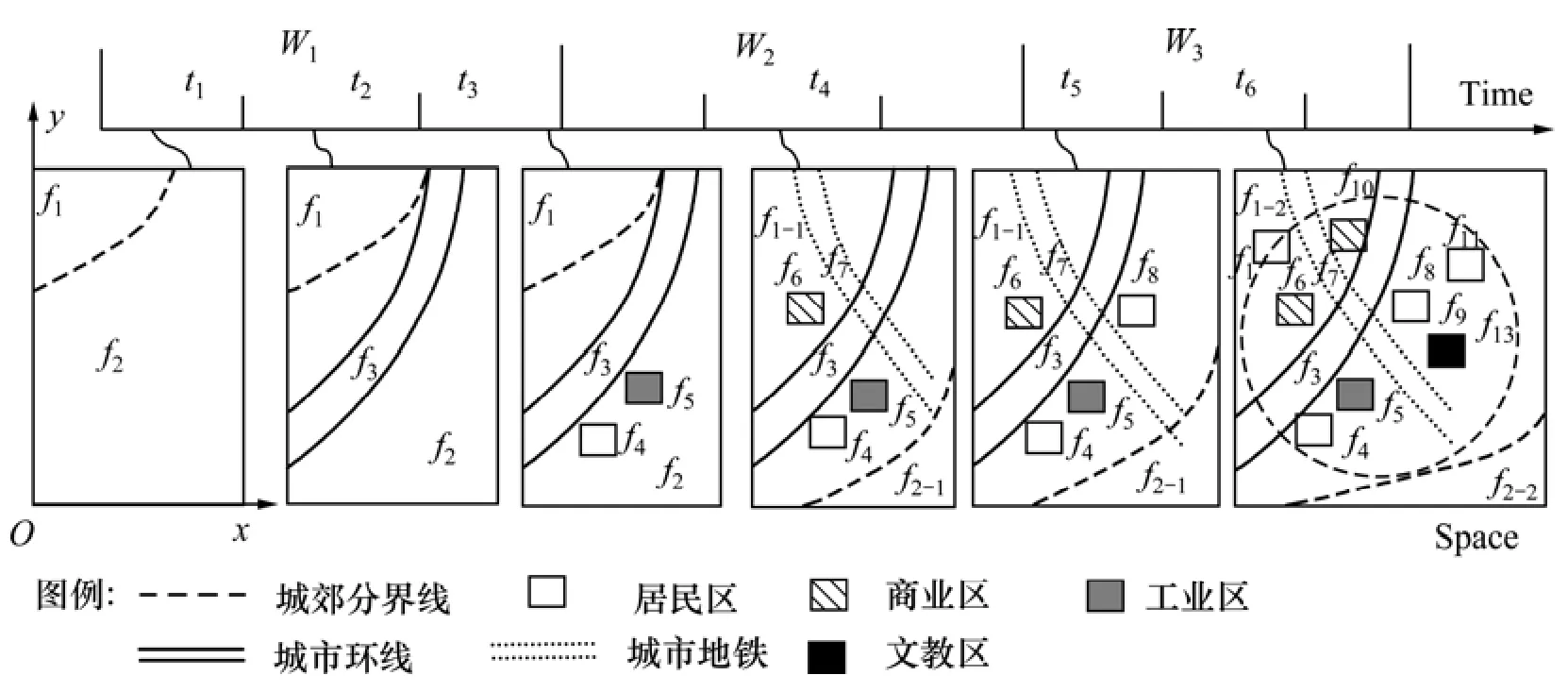
图4 时空数据实例的视图表示Fig.4 View of spatiotemporal database example

表2 时空数据的记录和存储机制Table 2 Records and storage of spatiotemporal data

4.2 规划要素关联模式挖掘过程

在规划进程中，规划要素权重的确定与要素的作用空间范围和时间效应有关。时空关联模式的挖掘过程(包括数据流程和算法)如表 3～5所示。其数据流程说明如下：

(1) 首先根据要素专题特性，对规划要素进行分类，内部按时间排序，见表3。

(2) 根据挖掘任务，检索出自身感兴趣的要素层，并计算N(Fi)/∑N(Fi)≥wminSup，见表 4。

表3 要素分类Table 3 Classification of features

表4 检索出的感兴趣的要素层Table 4 Interested feature layer

表5 时空要素关联索引矩阵Table 5 Indexed matrix of S-T association features

(3) 构建时空要素关联索引矩阵，见表5，其中，可以引入“要素权重”。

(4) 构建等价类，依需要搭建多元关联模式。可推导出：

对“星型”，

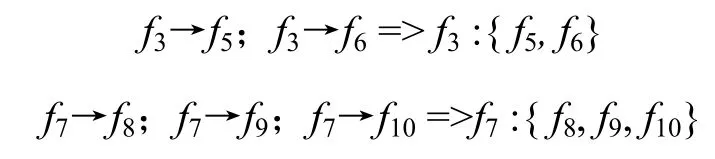
对“序列型”，

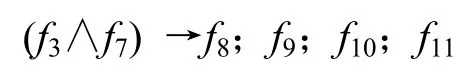
4.3 结果与讨论

在饱尝了城市恶性膨胀所带来的交通、能源和环境危机恶果之后，许多城市开始检讨其城市发展方向。Calthorp倡导的公交导向发展(TOD)策略逐渐被认同，是新都市主义在城市规划方面的实践模式之一[28]。这一模式主张城市规划应布置紧凑，以公共交通作为城市运行的支持系统，以公共交通(轨道交通、公交系统)节点作为城市规划发展的基础，围绕着公共交通站点布置城市服务设施(居住、商业、就业、教育等)。TOD模式在图4所示的时空视图中得到很好的诠释。

地铁和城市环路是城市化扩展非常重要的引擎。地铁和环路的交叉区域往往易形成非常重要的公共交通站点，进而引发大量的基础设施新建。样例中挖掘出f3:{f5;f6}和f3:{f8;f9;f10}等“星型”模式。忽略规划要素对经济GDP的影响，从TOD模式结合“星型”和“序列型”模式可以进一步探讨：(1) 城市进程的引擎动力于城市郊区的“规划城市环线”是否高于“地铁延伸至郊区”；(2) 规划城市环线某段的发展状况描述。可以用所挖掘“星型”模式的数量、热度和强度等来说明以上2点。

5 结论

(1) 在关联规则方面，提出了“要素关联规则”的新定义：一是空间对象扩展至地理要素；二是空间关系集合了距离、方位和拓扑等，以及时态关系。由“要素关联规则”新定义，提出了“多元”关联模式，即不同类型要素参与下的多关联规则的组合。在关联模式方面，图论表述了“星型”和“序列型”“多元”关联模式。最后，在挖掘算法上，引入了“等价类”，快速搭建“多元”关联模式。

(2) 本文只涉及 2种类型的关联模式，其发现的过程称为“显式”探索，即模式预先定义，在大量的关系实体中进行比配。另外，实例只用于说明挖掘的流程，并未在实际案例中得以实践。

(3) 下一步工作是进一步完善关联模式的类型和探讨有关“隐式”关联模式挖掘方法，并给予实证。当然，整合“地理经济要素(如GDP)与地理基础要素的约束关系”等关联规则，构建更复杂的“面向文本表达的地理知识”关联模式也有待于进一步研究。

[1] 杜宁睿, 李渊. 规划支持系统(PSS)及其在城市空间规划决策中的应用[J]. 武汉大学学报: 工学版, 2005, 38(1): 137-142.DU Ning-rui, LI Yuan. Planning support system (PSS) and its application to decision-making for urban spatial development[J].Engineering Journal of Wuhan University, 2005, 38(1): 137-142.

[2] Pandey G, Atluri G, Steinbach M, et al. An association analysis approach to biclustering[C]//KDD’09. Paris, France, 2009：677-686.

[3] Saha S, Bridges S, Magbanua Z, et al. Discovering relationships among dispersed repeats using spatial association rule mining[J].BMC Bioinformatics, 2008, 9(Suppl 10): 1-4.

[4] Lee I, Phillips P. Urban crime analysis through areal categorized multivariate associations mining[J]. Applied Artificial Intelligence, 2008, 22(5): 483-499.

[5] Huang Y, Kao L, Sandnes F. Predicting ocean salinity and temperature variations using data mining and fuzzy inference[J].International Journal of Fuzzy Systems, 2007, 9(3): 143-151.

[6] Chang C, Shyue S. Association rules mining with GIS: An application to Taiwan census 2000[C]//Fuzzy Systems and Knowledge discovery, FSKD’09. Tianjin, China, 2009: 65-69.

[7] Koperski K, Han J. Discovery of spatial association rules in geographic information databases[C]//Proceedings of the 4th International Symposium on Large Spatial Databases. Portland,ME: Berlin: Springer, 1995: 47-66.

[8] Zeitouni K, Yeh L, Aufaure M. Join indices as a tool for spatial data mining[C]//International Workshop on Temporal, Spatial and Spatiotemporal Data Mining. Berlin: Springer, 2000:102-114.

[9] Mennis J, Liu J. Mining association rules in spatio-temporal data:An analysis of urban socioeconomic and land cover change[J].Transactions in GIS, 2005, 9: 5-17.

[10] Yang H, Parthasarathy S. Mining spatial and spatio-temporal patterns in scientific data[C]//22nd International Conference on Data Engineering Workshops (ICDEW'06). IEEE Computer Society, 2006: x146.

[11] 曾玲, 熊才权, 胡恬. 关联规则在空间数据挖掘中的研究[J].计算机与数字工程, 2005, 33(6): 71-73.ZENG Ling, XIONG Cai-Quan, HU Tian. Research on association rules of spatial data ming[J]. Computer and Digital Engineering, 2005, 33(6): 71-73.

[12] 吕峰, 易晓峰. 用模糊遗传算法挖掘空间关联规则[J]. 武汉理工大学学报, 2006, 28(1): 96-104.LÜ Feng, YI Xiao-feng. Ming spatial association rule by fuzzy genetic algorithm[J]. Journal of Wuhan University of Technology,2006, 28(1): 96-104.

[13] 马荣华, 蒲英霞, 马晓冬, 等. GIS空间关联模式发现[M]. 北京: 科学出版社, 2007: 251-360.MA Rong-hua, PU Ying-xia, MA Xiao-dong. Mining spatial association patterns from GIS database[M]. Beijing: Science Press, 2007: 251-360.

[14] 张雪伍. 时空过程及其关联规则挖掘[D]. 上海: 同济大学测量与国土信息工程系, 2009: 128-134.ZHANG Xue-wu. Spatiotemporal process and its association rule mining[D]. Shanghai: Tongji University. Department of Surveying and Geo-informatics, 2009: 128-134.

[15] Sheng C, Hsu W, Lee M, et al. Discovering spatial interaction patterns[M]. Berlin: Springer, 2008: 95-109.

[16] Lee I. Mining multivariate associations within GIS environments[J]. Innovations in Applied Artificial Intelligence,2004: 1062-1071.

[17] Ding W, Eick C, Wang J, et al. A framework for regional association rule mining in spatial datasets[C]//Proceedings of the Sixth IEEE International Conference on Data Mining(ICDM’06). Hong Kong, 2006: 851-856.

[18] Yang H, Parthasarathy S, Mehta S. Mining spatial objectassociations for scientific data[C]//Proceedings of the 19th International Joint Conference on Artificial Intelligence (IJCAI).Edinburgh, UK. 2005: 902-907.

[19] Lee A, Chen Y, Ip W. Mining frequent trajectory patterns in spatial-temporal databases[J]. Information Sciences, 2009,179(13): 2218-2231.

[20] Huang Y, Xiong H, Shekhar S, et al. Mining confident co-location rules without a support threshold[C]//Proceedings of the 18th ACM Symposium on Applied Computing (ACM SAC).Melbourne, FL. 2003: 497-501.

[21] Agrawal R, Imielinski T, Swami A. Mining association rules between sets of items in large databases[J]. ACM SIGMOD Record, 1993, 22(2): 207-216.

[22] Han J, Pei J, Y Y. Mining frequent patterns without candidate generation[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data. Dallas, USA. 2000: 1-12.

[23] Lee H, Han J, Miller H, et al. Temporal and spatiotemporal data mining[M]. NewYork: IGI Publishing, 2007: 127-143.

[24] Tanbeer S, Ahmed C, Jeong B, et al. Efficient single-pass frequent pattern mining using a prefix-tree[J]. Information Sciences, 2009, 179(5): 559-583.

[25] Lee A J T, Liu Y H, Tsai H M, et al. Mining frequent patterns in image databases with 9D-SPA representation[J]. The Journal of Systems and Software, 2008, 82: 603-618.

[26] Zaki M J. New algorithms for fast discovery of association rules[R]. New York: Rensselaer Polytechnic Institute, 1997:10-24.

[27] 王静文. 空间句法理论的三维扩展及其应用研究[D]. 武汉:武汉大学测绘遥感信息工程国家重点实验室, 2006: 36-45.WANG Jing-wen. Syntax paraphrase for social dimension[D].Wuhan: Wuhan University. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, 2006:36-45.

[28] 焦点房地产网. 探索万年花城 TOD社区模式[EB/OL].[2008-06-16]. http://house.focus.cn.Focus on estate. Exploratory TOD community patterns[EB/OL].[2008-06-16]. http://house.focus.cn.