汇流宽度随集水面积变化的分布式水文模型

金 鑫，宋 颖，潘斌林

（桂林理工大学 环境科学与工程学院，广西 桂林541004）

传统的分布式水文模型在进行汇流计算时，将计算单元沿水流方向的宽度作为计算采用的汇流宽度。对于坡面汇流，该做法将坡面流从始至终作为片状薄层水流处理，而在实际中，坡面片状水流只是存在于汇流开始的阶段，由于水流的冲刷和侵蚀作用，片状水流很快就汇集成细沟流。根据研究，坡面细沟形成后，在细沟间距不变、雨强相同和坡度相等条件下，细沟不断增宽，沟内断面平均流速会随之减小，细沟宽度发展到一定程度后，细沟流流速与细沟泥沙起动流速相等，从而形成稳定的细沟宽度［1］。在通常的汇流模拟中，由于将以细沟流为主的坡面水流作为片状水流对待，坡面汇流计算的汇流宽度远远大于实际细沟流宽度的总和。在进行河道汇流计算时，传统的做法仍是将数字河道单元的宽度直接作为河道水流宽度对待，在进行单纯的产汇流模拟研究时，通过对汇流过程的一定技术处理，可以得到满足精度要求的水流过程，但据此得到的水流流速与实际流速有很大不同，模型无法进行较为准确的分布式输出，更谈不上分布式验证。而且在进行分布式土壤侵蚀模拟或其它与流域产汇流相关的研究时，由于计算的水流流速与实际情况差别较大，极大地影响相关模拟计算结果。为此，根据作者在黄土地区分布式土壤侵蚀模型研究中的体会，提出了考虑流域汇流宽度随集水面积变化的产汇流模型。

1 产汇流模型

1.1 流域概况及流域特征提取

研究区为位于伊洛河的东湾流域，该流域为以超渗产流为主要产流方式的黄土丘陵区。流域除出口水文站东湾站外，其上游还有栾川水文站，集水面积分别为2 657和239 k m2。流域特征提取以100 m栅格型DEM为数据源，流向判断采用D 8法［2］，洼地采用传统的填平法处理［3］。经过洼地处理之后，研究区域内所有网格的水流都可以经出口流出，形成连续的汇流网络。按照通常的做法，汇流网络可以确定研究区域内各栅格的上游累积网格数，当某栅格的上游累积网格数达到一定的集水面积阈值时，就认为该栅格为河道栅格。依次对研究区域内的所有栅格进行判断，就可以确定河道栅格，提取出数字水系。

1.2 超渗产流计算

产生径流的有效降雨等于实际降雨扣除降雨损失的部分。有效降雨由流域上的实际降雨以及蒸发蒸腾、林冠截留、填洼、土壤入渗等降雨损失而决定。由于研究区的降雨损失主要为林冠截留和土壤入渗，蒸发蒸腾和填洼损失量很小，可以忽略。因此，在产流的计算中，只考虑林冠截留和土壤入渗的降雨损失。

1.2.1 林冠截留计算 Dickinsoll［4］认为覆被最大截留量等于叶面积指数（LAI）乘以一个特定的存储值。降雨过程中冠层截留量主要和覆被的种类和生长时段有关，这一因素常常通过叶面积指数LAI来表达：

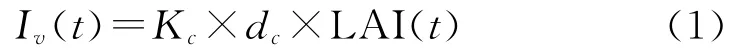
式中：Iv——冠层截留能力（mm）；Kc——冠层截留系数，与覆被类型有关；dc——覆被覆盖度，反映了覆被空间分布情况；LAI——叶面指数；t——计算时段。下同。

1.2.2 产流计算 超渗产流模型是应用下渗公式计算土壤下渗率f，然后依据霍顿下渗公式进行产流计算，计算方法为：

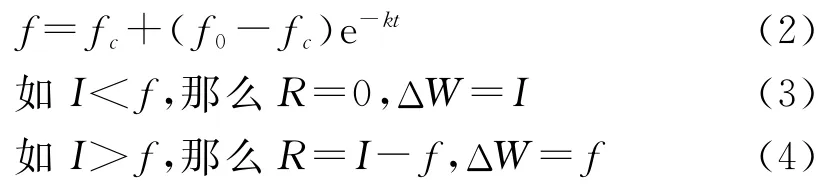
式中：f——下渗能力（mm/min）；f0——最大下渗能力 （mm/min）；fc——稳 定 下 渗 率 （mm/min）；k——下渗系数；I——雨强（mm/min）；R——径流（mm）；ΔW——表示单位时间内土壤含水量的增量（mm）。

因为下渗能力是土壤含水率的函数，土壤含水量的增量与下渗能力有如下关系：

根据霍顿公式，可得：

将（6）式带入（5）式，得：

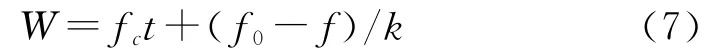
在实际计算中利用土壤含水量求下渗能力更为方便，故将霍顿下渗公式（2）与式（6）联立，消除时间项，得到下渗能力与土壤含水率的函数关系：

可根据下渗能力与土壤含水量的关系通过积分求得实际下渗量，进而求得产流量和时段末土壤含水量。

1.3 汇流计算

根据研究的对象和需要的不同，汇流过程可以用一维或二维的圣维南方程组来描述。对于平原区的汇流由于坡度较小，需要用二维模型来描述和模拟［5］；而对于山区性流域，一维圣维南方程组就能够满足模拟精度的需要。本文的研究区属山区性流域，其汇流过程可用一维圣维南方程组来描述。

对于宽度为B，长度为L，净雨强为Ie（x，t）的矩形坡面，用运动波来描述洪水波，用曼宁公式计算流速，圣维南方程组中的连续方程可写为如下形式：

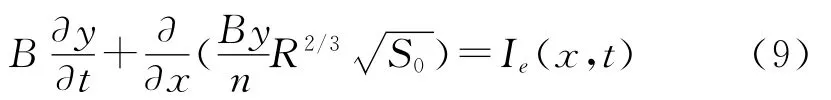
由于坡面上的水流属宽浅水流，可用水深h近似替代水力半径R，上式就成为关于水深的偏微分方程，利用Preissmann差分格式［6］对上式进行离散，得：

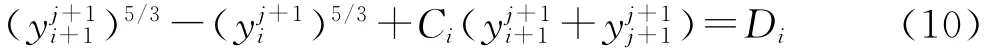
其中：

根据初始及边界条件，可得到一组关于水深的一元非线性方程，利用二分法及迭代计算可依次求得不同时刻各空间节点上的水深，由曼宁公式求得各节点上的流量、流速，得到该坡面的出流过程［7］。

对于有旁侧入流的河道单元，圣维南方程组中的连续方程可写为如下形式：

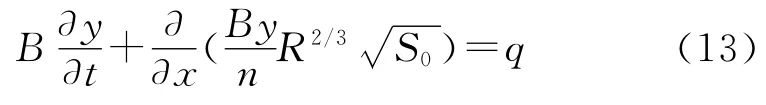
由于可根据河道形状及汇流宽度将水力半径表示为水深的函数，因此，上式也是关于水深的偏微分方程，对上式进行离散有：

式中：a——水力半径用水深表示后，连续方程中水深的指数。

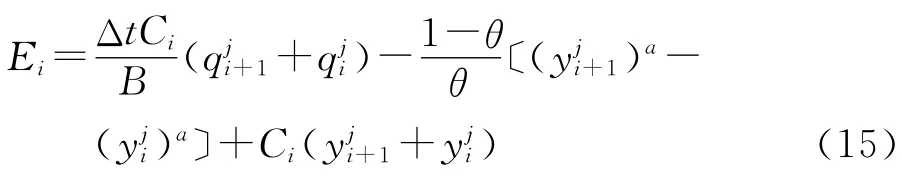
河道汇流采用与坡面汇流同样的方法得到一组一元非线性方程，最后得到河道单元的出流过程。

2 栅格单元汇流宽度的确定

在分布式水文模型的汇流计算中，常把实际水面面积等同于单元面积，即用单元尺寸代替实际的汇流宽度。这种假定只适用于自然条件下的2种特殊情况：一是坡面顶部产流时会有短暂的“片流”存在；二是流域中下游主河槽宽度刚好等于单元尺寸。

流速的大小不仅取决于河道的坡度，在流域的中下游更多地受到水位高差的影响。在分布式汇流计算中，一般只计算坡度对流速的影响，再加上DEM资料均化的影响，中下游计算出的流速往往偏小。为了拟合出口处的径流过程线必然要人为增大流速计算系数，从而导致流域上游的流量过程线集中且提前。

分布式汇流的主要目的是寻找坡面流速与坡度、植被等下垫面特性之间的关系，更细致的还涉及到水量的累积，即从坡顶到坡脚，水深与流量不断增加，但水深的增量不与流量的增量成正比，因为流速也同时增加了，有研究表明坡面上水深的增量与流量增量的3/2次方成正比［8］。

在忽略次网格汇流的情况下，单元上的过境水流从坡顶的片流逐渐汇聚成股，进入细沟、浅沟、切沟、小河直到大河，水流的集中程度逐渐增加。如果用单元内所用过水通道的宽度之和除以单元尺寸作为纵坐标，用集水面积或集水网格数量作为横坐标，就会得到一条曲线（见图1），即：在坡顶片流阶段过水宽度占满全部网格，对应曲线的“A”点；随着水流迅速汇聚成股过水宽度比例迅速减少，对应曲线的“B”点；当水流进入小河、大河时水流的集中程度仍然在增加，但由于集水面积的增加，水量也随着增加，需要更大的过水通道，在曲线中表现为从“C”点拐向“D”点；随着水量的进一步增加，河道宽度也随之增加，直到再次占满整个单元，即曲线中的“E”点；当集水面积很大时，相邻的几个网格都属于河道，此时对应着曲线中的“F”点。这条曲线可称为“汇流宽度曲线”。

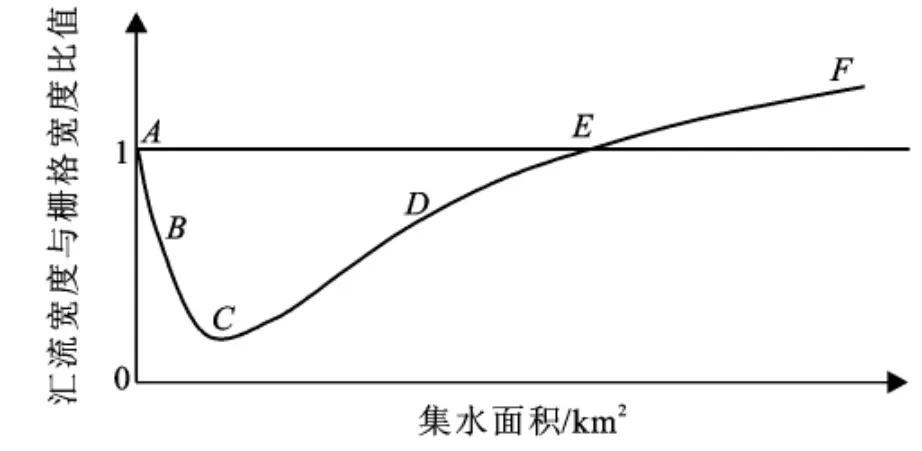
图1 设想的栅格汇流宽度随集水面积变化的曲线

2.1 汇流宽度曲线的建立

对于汇流宽度曲线，目前可以确定的是，该曲线一定存在一个等同于坡面单元宽度的起点A，一个水面宽度最小的转折点C，以及流域出口点F，但要确定A—C与C—F点之间曲线的确切走势，尚需一定的实测资料支持。但该曲线在A—C段逐渐下降、在C—F逐渐上升的趋势是存在的，也是理论上可以解释的。在A—C和C—F这2段的确切走势无法确定前，可暂时概化为直线。

对于只有一个出口站的流域，根据多年不同流量下实测的河宽资料，可以确定出过水通道宽度曲线的终点F，起点A的宽度即为坡面栅格的宽度；对于水面宽度最小的转折点C，其横坐标可以将其定为河道的阈值，而纵坐标就需要通过率定来确定。汇流宽度曲线对于提高汇流模拟以及产输沙模拟的精度是有实际意义的。

根据实测河宽资料得到东湾、栾川站的代表河宽分别为65和35 m。结合两站的集水面积2 684和338 k m2，就得到了过水通道宽度曲线中的2个点；研究区的坡面－河道阈值为10 k m2，这样得到一个东湾流域简化的汇流宽度曲线（该曲线反映的是进行汇流计算时所采用的水流宽度，并不是真正的水流宽度，见图2）。

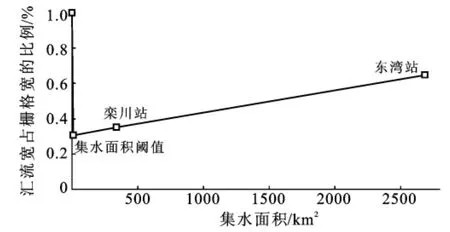
图2 东湾站（含栾川）的汇流宽度简化曲线

得到图2的汇流宽度曲线之后，分布式汇流计算中可以根据单元水量计算出相应的水深，根据曼宁公式计算出流速。相对于以前不考虑汇流宽度沿程变化的方法，该方法在理论上更合理一些。

2.2 汇流宽度曲线的意义

（1）统一坡面汇流参数与河道汇流参数。为了描述水流集中、水量累积等因素对汇流的影响，在分布式汇流中常通过两套不同的参数对坡面汇流与河道汇流分别计算，二者通过集水面积阈值来区分。水流从坡面流到河道水流是一个连续的过程，用汇流宽度曲线来描述更加合理，而且不再需要两套不同的参数。

（2）便于确定合适的DEM分辨率。当区域的集水面积在“E”点左侧时，河道汇流与坡面汇流的计算方法都符合流域特征提取时最陡坡度法中唯一出口的假定；当集水面积在“E”点右侧时，就会同时有若干相邻网格有水流通过，这需要同时改变流域特征提取方法和河道汇流计算方法。因此，可以把“E”点作为确定DEM分辨率的指标：只要能够保证计算区域出口处的集水面积在“E”点左侧，就可以取更小的分辨率。

（3）计算水位、矫正流速后计算输沙。分布式水文模型的水流流速并不是计算真正的流速，它包含了影响出口处汇流结果的所有误差；而在输沙计算中，流速误差将以几何级数传递到携沙能力的误差中［9］。汇流宽度曲线的使用，使得不同网格的流速计算相对于原来更趋合理，有理由进一步降低输沙计算的误差。

（4）划分坡面单元细沟和细沟间的比例、沟道单元沟道和坡面的比例，避免在单元栅格内只进行单一方式侵蚀计算带来的误差，提高侵蚀产沙计算的精度。

（5）汇流特征宽度及其空间分布的引入，除了细化水量－流速关系外，还为坡面流再入渗的描述、直接产流面积（水面面积）时空变化的描述提供了可能。

3 模型应用

选择东湾和栾川2站有同步资料的场次洪水19810714和19831003，使用本文所建立的产汇流模型，对东湾站的洪水过程进行模拟，把东湾站的洪水过程线拟合好之后，在对应栾川站位置的单元上可以同时得到栾川站的过程线，并用同一套参数直接模拟栾川站的洪水过程，模拟结果见表1。另外，对上述2场洪水，按照传统方法，不考虑汇流宽度随集水面积的变化，直接用栅格宽度代替汇流宽度进行汇流计算，两站的模拟结果见表2。

表1 考虑汇流宽度变化的模拟结果

表2 不考虑汇流宽度变化的模拟结果

从东湾站的模拟结果来看，两种方法的模拟精度大致相当，而对栾川站的模拟，两种方法所模拟的精度有较大差别。从栾川站的模拟结果可以看出，考虑汇流宽度随集水面积变化的模拟方法，其精度虽不十分令人满意，但比传统方法的精度有较大提高，且计算的洪水过程与实测更为接近。考虑汇流宽度变化直接进行栾川站的洪水模拟过程见图3—4，不考虑汇流宽度变化直接进行栾川站的洪水模拟过程见图5—6。

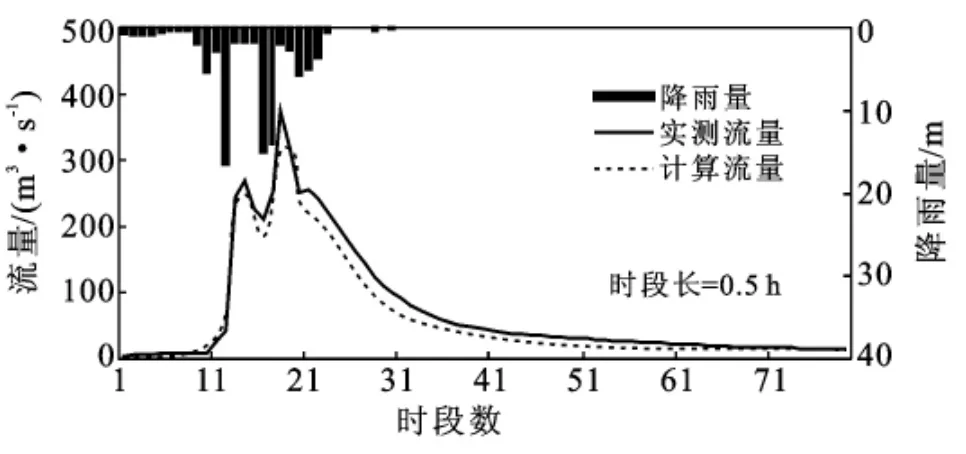
图3 考虑汇流宽度变化的栾川站19810714洪水过程

图5 不考虑汇流宽度变化的栾川站19810714洪水过程

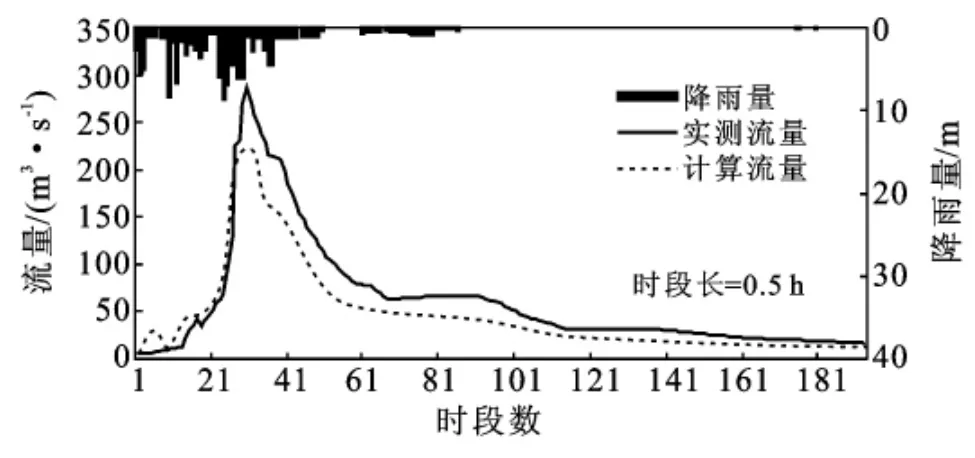
图4 考虑汇流宽度变化的栾川站19831003洪水过程

图6 不考虑汇流宽度变化的栾川站19831003洪水过程

4 结论

汇流宽度随集水面积变化的分布式产汇流模型与传统分布水水文模型的不同，在于使用了汇流宽度曲线，通过该曲线对不同集水面积的栅格汇流宽度进行确定，改变了传统方法将栅格宽度直接作为汇流宽度的做法。虽然汇流宽度曲线变化的确切趋势尚需大量的实测资料进行验证，但从东湾流域的应用情况来看，汇流宽度曲线的引入，使坡面汇流和河道汇流可以使用统一的汇流参数，并且在一定程度上提高了分布式输出的精度。

［1] 杨具瑞，曹叔尤，刘兴年，等.黄土坡面细沟侵蚀稳定宽度的动力学研究［J］.昆明理工大学学报：理工版，2004，29（4）：159－163.

［2] O＇Callaghan J F，Mark D M.The extraction of drainage net works from digital elevation data.［J］.Computer Vision，Graphics，and Image Pr ocessing，1984，28：323－344.

［3] Jenson S K，Do mingue J O.Extraction topographic str ucture fro m digital elevation data f or geographic information system analysis［J］.Photogrammetric Engineering and Remote Sensing.1988，54（11）：1593－1600.

［4] 王加虎.分布式水文模型原理与方法研究［D］.南京：河海大学，2006.

［5] Giammarco P D，Todini E，Lamberti P.A conservative finite elements approach to overland flow：The control volu me finite element for mulation［J］.Journal of Hydrology，1996，175：267－291.

［6] 张建云.水文学手册［M］.李纪生，译.北京：科学出版社，2002.

［7] 李丽.分布式水文模型的汇流演算研究［D］.南京：河海大学，2006.

［8] Wood E F，Hebson C S.On Hydrologic si milarity 1：Derivation of t he di mensionless flood frequency cur ve［J］.Water Resour Res.，1986，22（11）：1549－1554.

［9] 中国水利学会泥沙专业委员会.泥沙手册［M］.北京：中国环境科学出版社，1992.