基于双闭环控制的降压型DC/DC转换器仿真

吴 超，陈 博，曾 程，黄 亮

(武汉理工大学自动化学院，湖北 武汉 430070)

随着各种便携式电子产品的飞速发展，PWM开关电源得到广泛运用。在PWM开关电源中，开关电源系统的建模和分析是研究开关电源的拓扑结构和控制方法的基础。但其属于周期性时变非线性系统，含有多变量的特点使得开关电源的建模成为一个难题。由于时变、非线性均出现在功率级，因而功率级建模是开关电源建模的难点所在[1-2]。

笔者从Buck降压型开关电源的拓扑结构各功率开关的线性等效电路入手，对Buck转换器的功率级进行建模，研究功率级的传递函数，进而进行Matlab仿真，根据仿真结果，设计了平均电流模式控制的降压PWM开关电源系统。

1 Buck主电路的线性等效电路

图1给出了Buck降压型转换器的电路原理图。

图1 Buck电路原理图

在图1中，开关管VT为主开关，二极管DT为辅助开关，Rc为滤波电容C的等效寄生电阻。对于理想的Buck拓扑变换器，其输入电压与输出电压的比为1∶D，其中D为占空比，电感的平均电流与电源的平均电流比为1∶D。因此在连续模式下，主开关管与辅助开关管就形成了一个非隔离型的变压器，得到如下关系式[3-7]:

对式(1)和式(2)进行扰动量叠加得:

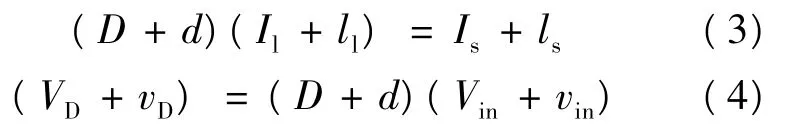
式中:VDT为二极管DT两端电压;Is为通过开关管VT的电流;Il为电感的电流。令D、Il、VDT、Vin、Is为电路的稳态分量;d、il、vDT、vin、is为 D、Il、VDT、Vin、Is的扰动分量，并依据小信号的3个假设将式(3)与式(4)化简得到:

由此得到Buck电路的线性等效电路图如图2所示。

由图2小信号模型，可以导出Buck电路在连续模式(CCM)下的传递函数。

(1)令Vin=0，d(s)对vo(s)的传递函数为:

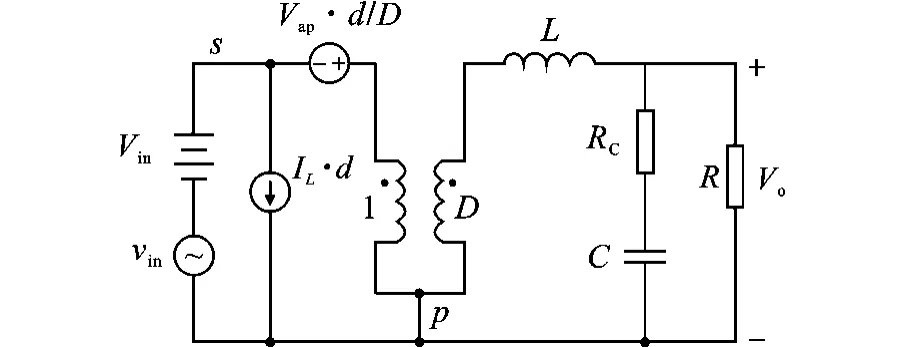
图2 Buck线性等效电路

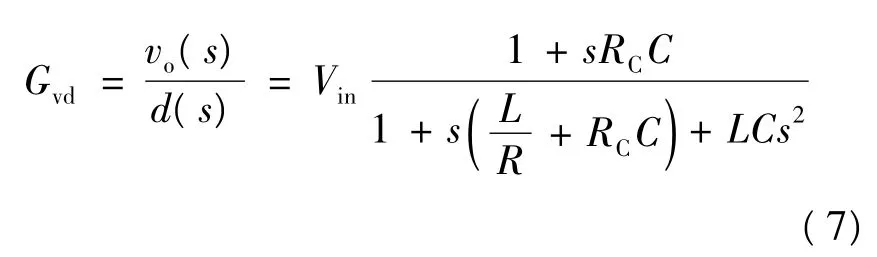
(2)令Vin=0，则d(s)对is(s)的传递函数为:

(3)输出vo(s)对输入vin(s)的传递函数Mv为:

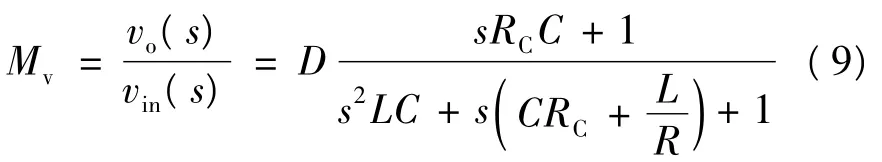
(4)令vo(s)=0，d(s)=0，得开环输出阻抗的传递函数为:

(5)开环输入阻抗为:

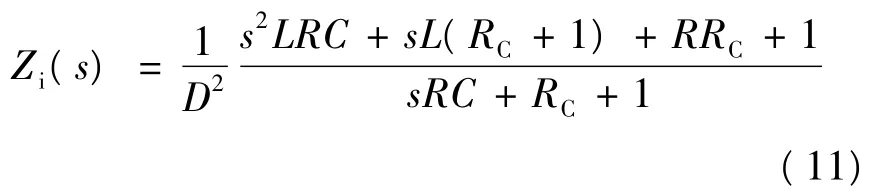
至此，Buck拓扑降压型的小信号模型已经建立，为后面的补偿网络设计做好了准备。

2 平均电流控制的补偿网络设计

为了使电路在恶劣的环境下稳定工作，必须选择合适的反馈网络，使系统有充足的裕量与合适的截止频率。为使系统稳定，笔者采用平均电流模式控制。其突出的优点如下[8-10]:①具有高增益的电流放大器，平均电流可以精确地跟踪电流设定值;②噪声抑制能力强;③无须斜坡补偿;④平均电流法可应用在任意电路拓扑。控制电路包含两个负反馈环路:内环为由电流检测放大器、电流调节器、占空比调制器和功率级组成的电流控制环;外环则是包含了电阻分压器、误差放大器、电流调节器、占空比调制器和功率级的电压控制环。基于平均电流控制的PWM降压开关电源系统的完整模型如图3所示。

图3 基于电压外环电流内环模式控制的Buck开关电源系统图

3 实例分析

笔者设计了一个Buck型DC/DC转换器。电路参数如下:输入电压为60～100 VDC，输出电压为48 VDC，输出滤波电感为250 μH，滤波电容为200 μF，工作频率为 20 kHz，电容等效串联电阻SER为0.15 Ω。负载 R=4 Ω，FM 近似等于1/2.5。如果仅采用比例反馈，其开环频率特性如图4所示。

图4 比例补偿后的系统频率特性

由图4可看出，系统的截止频率fc=2.99 kHz，相位裕量仅为8°，系统的稳定性很差。因此需要采用适当的反馈网络，使电路获得良好的性能，笔者设计的电流环采用单极点-单零点的补偿电路，得到如图5所示的电流环补偿后电压环开路的开环频率特性图。

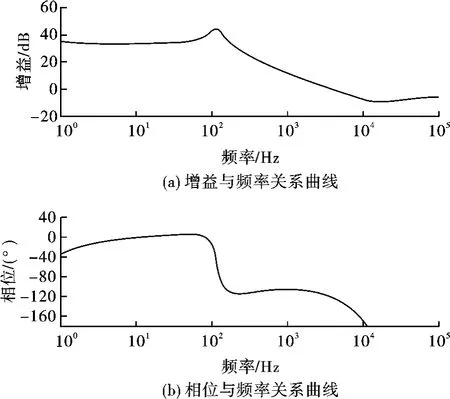
图5 电流补偿后的电压环开路频率特性

系统低频段增益比较高，带宽为500～400 Hz时，有一定的中频带。0 dB穿越点在3.5 kHz处，小于开关频率的1/5;而且穿越点为-1特性，相位裕量为70°;有一定的增益裕量。从控制理论的角度看该系统的电流环稳定性是没有问题的。

建立了电流环模型后，再建立电压环，电压环同样采用单极点-单零点补偿器，得到电压环开路的频率特性如图6所示。

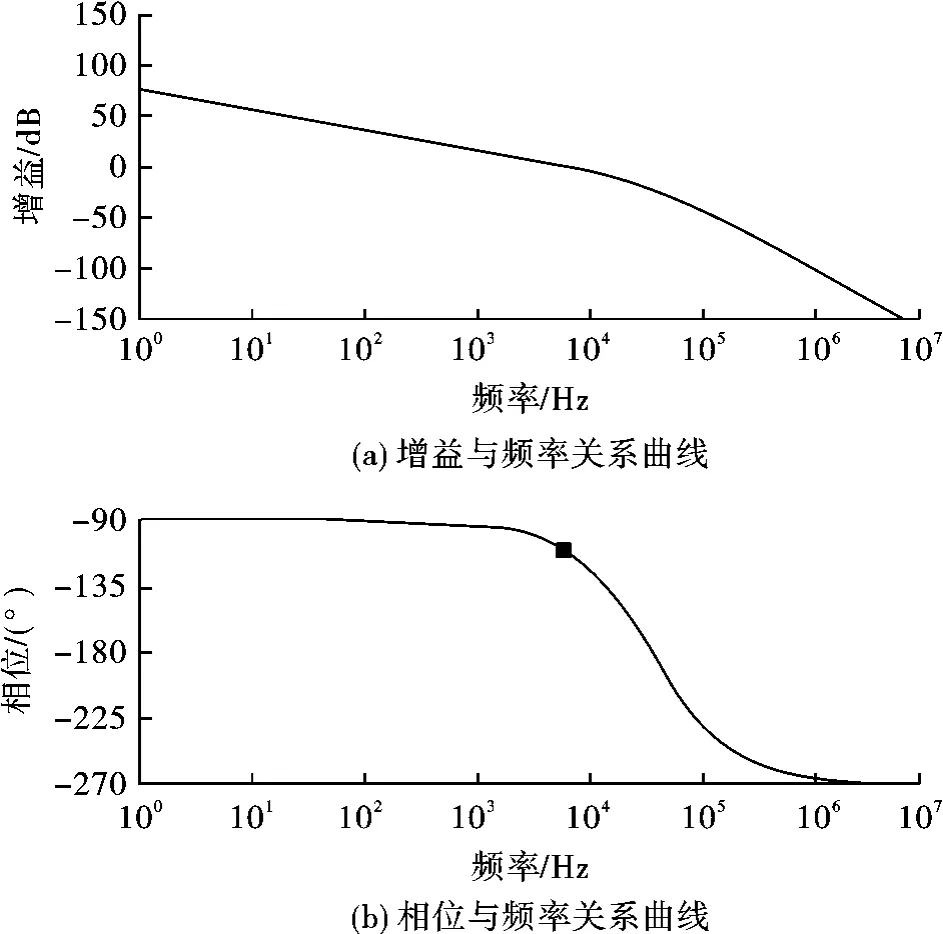
图6 电压控制环开环传递函数的频率特性

对电压环进行Matlab仿真，结果由图6可见:

(1)在低频段，幅频特性的下降斜率为-20 dB/dec，系统的静态误差为零。

(2)在中频段，幅频特性的下降斜率为-20 dB/dec，系统有足够的相频裕度，因此电压环一定是稳定的。

(3)在高频段，幅频特性的下降斜率为-40 dB/dec，系统有较强的抗干扰能力。

(4)系统截止频率为5.91 kHz，相位裕度为69°，满足设计要求。

4 结论

开关变换器采用电流电压双闭环控制模式后，由开环系统的幅频特性可知，双闭环系统在高频段的衰减十分明显，这将大大降低噪声的干扰。由于开环相位裕量较大，系统的瞬态响应将得到改善，电源设计完全满足要求。

[1] 毛鸿，吴兆麟，沈琦.高精度开关稳压电源的系统分析与设计[J].电力电子技术，1999，33(2):12-14.

[2] 赵涛，王相綦，尚雷，等.高性能开关型直流稳压电源的设计[J].核技术，2004，27(9):64-66.

[3] BELLOMO P，DE LIRA A.SPEAR 3 large dc magnet power supplies[C]//Proceedings of EPAC 2004.Lucerne:[s.n.]，2004:801-803.

[4] SUH J H，HA K M，JEONG S H，et al.Performance of the PLS high precision magnet power supplies[C]//Proceedings of LINAC 2002.Gyeongju:Pohang Accelerator Laboratory，2002:505-507.

[5] VLATOKOVI'C V，SABAT J A，RIDLEY R B，et al.Small signal analysis of the phase shifted PWM converter[J].IEEE Transactions on Power Elect ronics，1992，7(1):128-134.

[6] VATCHE V.Simplified analysis of PWM converters using model of PWM switch part I:continuous conduction mode[J].IEEE Transactions on Aerospace and E-lectronic Systems，1990，26(3):490-496.

[7] MARIANK K.Transfer function of current modulator in PWM converters with current-mode control[J].IEEE Transactions on Circuits and Systems，2000，47(9):1407-1412.

[8] PHILIP C.Modeling average current mode control[J].IEEE，2000(2):256-262.

[9] 石健将，王慧贞，严仰光.DC/DC模块电源并联研究[J].电力电子技术，2002，36(3):43-45.

[10] 杨汝.平均电流模式的控制电路设计[J].电力电子技术，2002，36(4):56-59.