激光干涉条纹锁定系统的设计与实现
2011-08-01易迎彦杨应平
易迎彦,杨应平
(武汉理工大学理学院,湖北 武汉 430070)
自20世纪60年代以来,由于激光的出现和电子技术的日益成熟,激光干涉仪因其非接触测量、精度高、稳定性好和易于实现等优点,得到了广泛的应用[1-4]。通常,干涉仪在不采用光学倍频和条纹细分技术情况下是以λ/4波长为计量单位。为测量 λ/4波长以下的位移,如测量10-7/℃以下材料的线膨胀系数[5]、地面低频微振动[6]和引力波探测[7]等,需要进一步提高干涉仪的测量精度,为此设计了激光干涉条纹锁定系统,该系统由激光器及稳频装置、干涉系统、检测及控制电路、位移反馈执行机构(压电陶瓷),以及数据采集系统组成。与一般干涉仪系统相比,采用调制法后整个干涉仪系统工作在高频段,大大降低了电路的1/f等噪声影响[8]。将干涉仪工作点锁定在暗点及干涉极小位置,可抑制光散粒噪声。
1 激光干涉条纹锁定系统工作原理
激光干涉条纹锁定系统由激光干涉系统、检测及控制电路、数据采集系统3部分组成,如图1所示。激光干涉系统为一个常用的迈克尔逊干涉仪,由兰姆凹陷稳频激光、分束镜、两个反射镜M1、M2和光电探测器PD(RS Ltd.OSD15-5T)等器件构成。检测及控制电路由信号发生器、2F带阻滤波器、1F带通滤波器、乘法器、低通滤波器、PI调节器以及PZT(其中PZT1用作调制,PZT2用作反馈执行机构)等构成。数据采集系统包括16位A/D、晶振时钟电路及PC计算机。
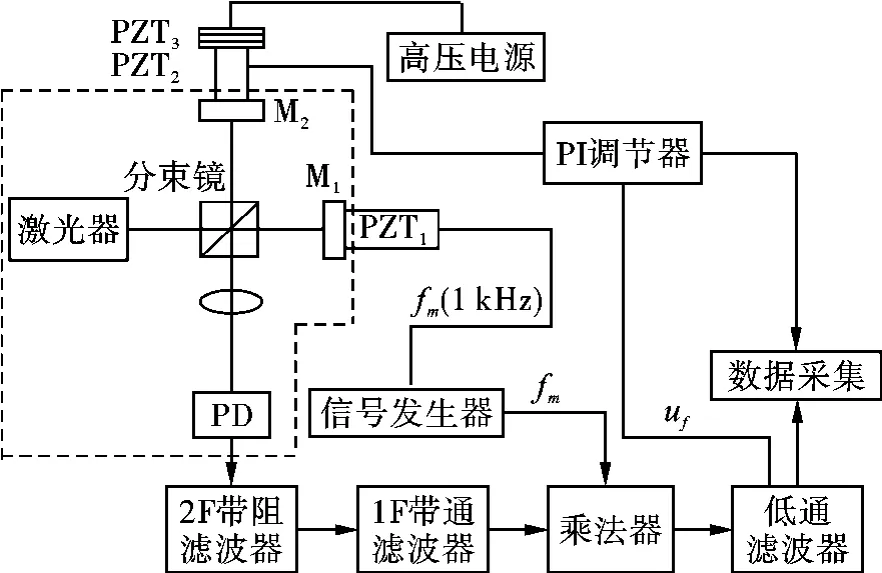
图1 激光干涉条纹锁定系统原理图
激光干涉条纹由透镜汇聚到光电探测器上。信号发生器产生的高频fm(设为1 kHz)正弦信号送到PZT1上,使PZT1的长度做频率为f的伸长缩短的周期运动,从而使得其光电探测器PD记录的干涉光强也随之发生周期性的变化,将这种工作在高频的干涉系统称为激光干涉调制测量系统。该系统加上一个位移反馈执行机构便构成一个常用的激光干涉锁定系统。如图1所示PZT2为位移执行机构,通过检测控制系统反馈一电压给PZT2,从而改变M2的位置,始终维持M2与M1的光程差不变。鉴于光散粒噪声抑制考虑,通常激光干涉锁定系统维持在干涉极小位置(暗点)[9-10]。
对于一般的激光干涉系统而言,光电探测器输出的干涉信号为:
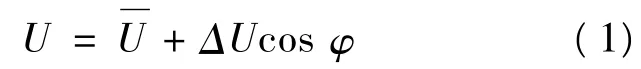
当在PZT上加一正弦调制信号,则光电探测器的输出为:
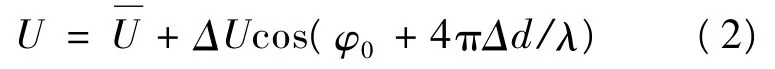
其中:Δd=xmsin ωt+Δx;ω 为所加调制信号的频率;xm为调制PZT最大伸长量,它依赖于调制PZT1的压电常数和调制电压的幅度um;Δx为其他因素引起的位移改变,在未施加外部激励信号情况下,为外部振动噪声引起的位移。利用三角恒等式变形可得到:
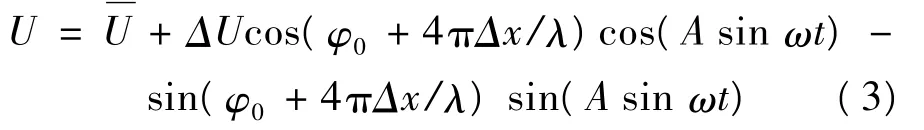
其中,A=4πxm/λ。利用贝赛耳函数将上式展开可得:
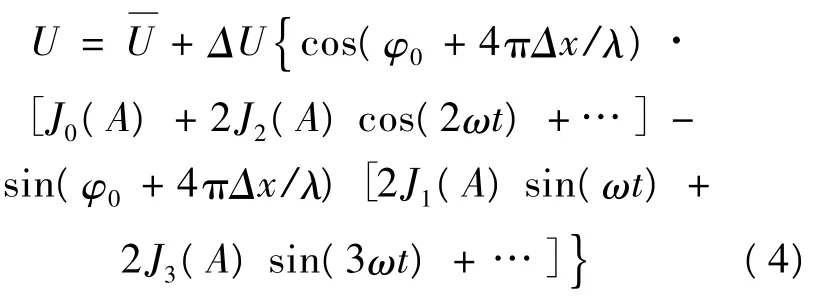
当A较小时,探测器输出的光强信号可近似表示为:
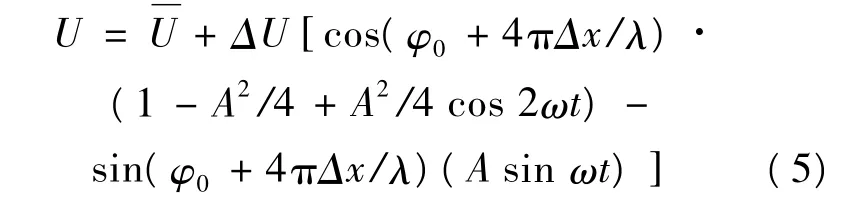
从式(5)可看出中括号中的第一项由ω的二倍频和常数项组成,第二项只有基频信号。
为抑制二倍频信号,从光电探测器PD输出的信号先通过一个2F带阻滤波器,滤波器的中心频率选择在2 kHz。为了滤掉直流、二倍频以及基频频带以外的噪声,在带阻滤波器后面接有一个1F带通滤波器。带有低频信号的1F载波信号与本地的1F参考信号经过一个乘法器(AD734)进行乘法计算,即解调。乘法器的输出经一个低通滤波器,将所得误差信号累加反馈给PZT2。当对干涉条纹以频率fm(基频)进行调制时,如果光电探测器工作在“暗点”,则所接收到的光强以及相应的输出电流iPD均是严格的二次谐波,如图2(a)所示;如果干涉条纹产生微小位移,光电探测器工作位置偏离“暗点”,由式(5)可知,输出的电信号除了含有二次谐波成分外,还含有一次谐波成分,如图2(b)和图2(c)所示。一次谐波分量的大小和相位直接反映干涉条纹移动的大小和方向。通过乘法器进行相位锁定,所得的误差信号一方面经过负反馈系统输送到PZT2驱动器,另一方面输出送到信号记录与处理系统。由于干涉条纹的移动,反映了干涉臂长度位移的相对变化,因此通过改变PZT2工作电压对这一变化进行补偿,可使条纹朝相反方向移动并回复到平衡位置,即光电探测器的工作点得到锁定[11]。
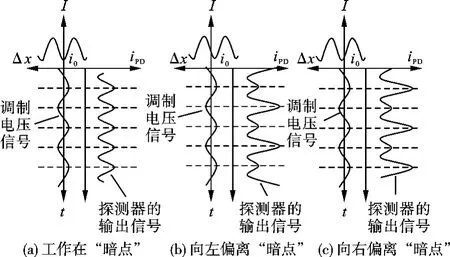
图2 光电探测器输出电流图
探测器的光强信号经过2F带阻滤波、1F带通滤波、乘法器解调以及随后的低通滤波后,输出电压信号为:
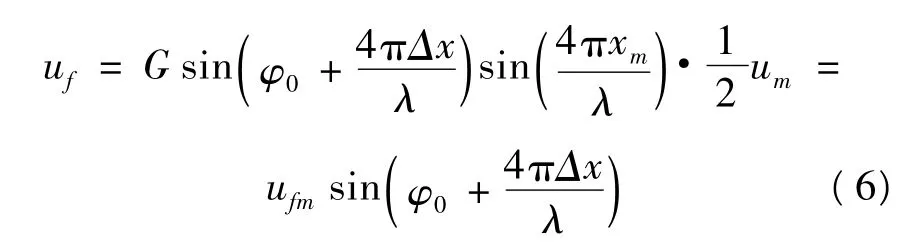
2 实验结果分析
2.1 激光干涉条纹锁定系统的检验
为检测整个反馈控制系统是否处于正常工作状态,笔者在反馈PZT2后面又串联了一个PZT3,用一高压电源给该PZT3加电压,使其产生一定量的位移,然后将电路中的低通输出信号和反馈给PZT2的电压信号同时送入到数据采集卡中进行记录,如图3所示。
检测PZT3为一薄圆片状,其直径为(28.00±0.02)mm,厚度为(3.00±0.02)mm。图3的实验结果是在采样频率为1 Hz,两次给检测用的薄片PZT3施加(132±1)V电压驱动下系统的反馈信号和低通输出信号。从图3(a)可知,反馈信号的变化量为Δu=(18.5±1.0)V,而反馈PZT2的定标结果为Sp=(4.8±0.1)×10-9m/V。由此可得,反馈 PZT2移动的位移量为 Δx=Sp×Δu=(88.8±5.1)×10-9m。同样可通过利用检测薄圆片状PZT3的压电系数计算出检测薄圆片状PZT3的位移量。用于检测的薄圆片状PZT3的压电系数为d33=(6.3±0.3)×10-10m/V,由Δx'=d33V可得,用于检测的PZT3在所加驱动电压下移动的位移量Δx'=(83.1±4.0)×10-9m。在误差范围内Δx与Δx'相等,即反馈的位移量与外界激励的位移量一致。由此可判断该系统处于较好的工作状态。事实上,如果将用作检测的PZT3作为样品,而已知反馈PZT2的压电常数或者灵敏系数则可以用该方法对样品的压电常数进行标定,也为较小的微位移量提供了一种定标的方法。
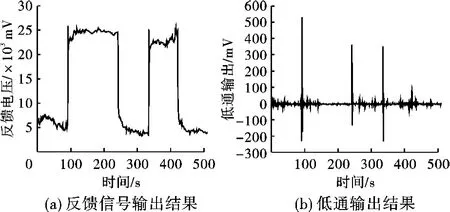
图3 激光干涉条纹锁定系统的检验结果
2.2 激光干涉锁定结果分析
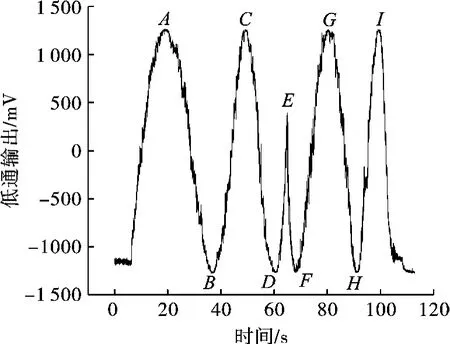
图4 低通输出曲线
为分析激光干涉仪锁定结果,在开环情况下,用一高压电源给反馈PZT2逐渐加电压,直到观测到干涉信号出现几次极值以后逐渐减小到零,记录的低通输出曲线如图4所示。图4中从起始点到相位突变点E处对应为给反馈PZT2所加电压逐渐增加的过程,E点后面的曲线对应驱动电压逐渐减小到零的过程。将图4中A、C、G、I点处的最大值平均作为低通输出的最大值(1 255±5)mV,同样将B、D、F、H处的最小值平均作为低通输出的最小值(-1 260±5)mV。最后将最大值和最小值之差的50%作为低通输出的幅度ufm=(1 258±5)mV。
下面分别对1 Hz和100 Hz采样的锁定结果进行分析。图5(a)是在安静情况下,采样频率为1 Hz时的低通输出结果,由图5(a)可知,在前40 min时环境处于相对安静状态,而40 min以后其残差噪声明显增加,这是由于在以后的时间离测量地点较近处机床工作的缘故。在安静段的残差信号为(-3±10)mV。由干涉仪工作在暗点有φ0=π,则由式(6)可写为:
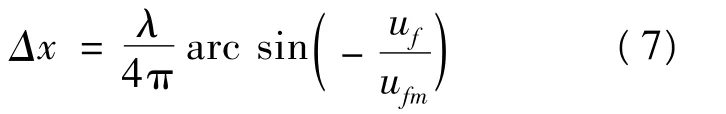
将测量残差信号的标准方差uf=10 mV和上面所测得的低通输出信号幅值ufm=1 258 mV代入式(7)可得这意味着,在采样频率为1 Hz时,安静情况下干涉仪在0~0.5 Hz带宽内的分辨率达到λ/1 500的水平。利用式(7),将低通输出的残差信号转换为位移信号,得到如图5(b)所示的位移幅度功率谱密度,由该图可知,在0~0.1 Hz频段内干涉仪的分辨度可达到
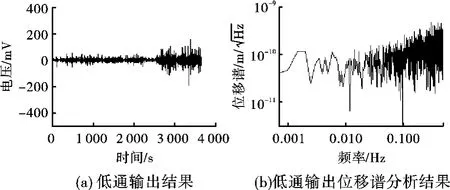
图5 采样频率1 Hz时锁定结果
图6(a)是在安静情况下,采样频率为100 Hz时的低通输出结果,最后低通输出的残差信号为(-3±36)mV。由式(7)可以得到在100 Hz采样频率下干涉仪分辨率约为λ/400,即干涉仪在0~50 Hz的频带内的分辨率可达到λ/400水平。采用同样的方法可得到如图6(b)所示的残差信号幅度功率谱密度。由该图可知,在3~8 Hz频段内干涉仪的分辨率可达到值得说明的是,由于干涉仪系统及其外界的干扰作用,使得干涉仪的长期测量精度还达不到这个水平,在安静环境条件下干涉仪的长期测量精度可达到λ/100水平。为了进一步提高干涉仪的精度在纳米及其以上水平,需要增补隔振和温控装置。
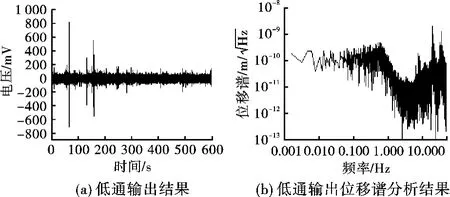
图6 采样频率100 Hz时锁定结果
3 结论
设计并研制了用于锁定激光干涉条纹的电路检测及其控制系统,包括激光干涉系统、检测及其控制电路、位移反馈执行机构,以及数据采集系统。干涉仪锁定结果表明,在0~0.5Hz的频带内(即1Hz采样时),其干涉仪的分辨度达到λ/1 500水平;而在0~50Hz的频带内(采样频率为100 Hz时),其干涉仪的分辨度达到λ/400水平。对应的幅度功率谱密度表明在0~0.1Hz和3~8Hz频段内干涉仪的分辨度分别达到和水平。由于干涉仪系统受外界的干扰作用,使得干涉仪的长期测量精度仅达到λ/100量级水平。
[1] CHEN J,ISHII Y,MURATA K.Heterodyne interferometer with a frequency-modulated laser diode[J].Appl Opt,1998,27(1):124-128.
[2] LI J F,MOSES P,VIEHLAND D.Simple high-resolution interferometer for the measurement of frequencydependent complex piezoelectric responses in ferroelectric ceramics[J].Rev Sci Instrum,1995,68(1):215-221.
[3] WANG X Z,SASAKI O S.Measurement of small vibration amplitudes of a rough surface by an interferometer with a phase-conjugate mirror[J].Appl Opt,2000,29(5):4593-4597.
[4] WANG X F,WANG X Z,QIAN F,et al.Laser diode interferometer used for measuring displacements large range with a nanometer accuracy[J].Opt& Laser Technol,2001,33(4):219-223.
[5] 严琴,李东风.低膨胀固体材料线膨胀系数的干涉测量方法[J].激光技术,2004,28(2):202-204.
[6] ZHOU Z B,LUO J,YAN Q,et al.Seismic noise effect on equivalence principle test using free-fall interferometry[J].Chin Phys Lett,2001(18):10-12.
[7] SAULSON P R.Fundamentals of interferometric gravitational wave detectors[M].Singapore:World Scientific,1994:26-127.
[8] 易迎彦,周泽兵.压电陶瓷压电特性的激光调制法测量研究[J].应用光学,2004,25(3):27-32.
[9] BRACCINI S,BRADASCHIA C,COBAL M,et al.An improvement in the vibration isolation GRO super-attenuator for interferometric detection of gravitational waves:the using of a magnetic anti-spring[J].Rev Sci Instrum,1993(64):310-315.
[10] BRACCINI S.BRADASCHIA C,FABBRO R.et al.Design and operation of an interferometer developed to test the suspensions of the Virgo gravitation wave antenna[J].Phys Lett A,1993(173):252-256.
[11] 罗俊,范淑华,蔡惟鑫.地壳应变的激光干涉调制法测量[J].地壳形变与地震,1994,14(2):76-81.
