应用纤维单元模型的钢筋混凝土框架结构损伤与失效分析
2011-08-01徐龙河李忠献
吕 杨,徐龙河,李忠献,丁 阳
(1. 天津大学建筑工程学院滨海土木工程结构与安全教育部重点实验室,天津 300072;2. 北京交通大学土木建筑工程学院,北京 100044)
在历次大地震中[1-2],大量建筑结构发生严重破坏甚至倒塌.分析结构失效过程及失效模式对避免结构坍塌、减轻地震人员伤亡具有重要意义,同时,结构失效分析也是进行震后灾害评估和重建的重要依据.结构失效过程分析主要步骤有:①进行强震作用下结构响应分析,目前,结构分析主要有静弹性分析、动弹性分析、静弹塑性分析和动弹塑性分析.强震作用下,建筑结构进入强非线性响应阶段,弹性分析方法一般不能满足工程结构分析精度要求,静力弹塑性分析由于不能考虑地震的动力效应和损伤的累积效应,不适合用于结构强震作用下的失效过程分析.结构动力弹塑性分析能较好地模拟地震作用下结构动力响应,根据结构数值模拟方法不同,可分为实体单元模型、梁单元模型、塑性铰单元模型和纤维单元模型等多种形式,其中纤维单元模型[3-4]能以较低的计算成本获得很高的求解精度.②建立材料或构件局部的损伤准则.由于钢筋混凝土结构由混凝土和钢筋两种完全不同的材料复合而成,目前两种材料的损伤准则还没有合理的组合方式,大多直接建立构件层次[5]的损伤准则.③建立结构层或结构整体[5-6]的损伤准则.结构整体损伤准则定义为构件损伤指数加权组合或受损结构动力特性(如结构频率、振型、刚度等)的变化,由于结构整体动力特性的变化不能精确地确定结构损伤部位,不适合用于结构失效过程分析,目前,整体损伤准则大多以局部损伤指数加权组合的方式定义.④结构失效模式分析.对结构重新设计或增设控制装置以优化结构失效模式,提高结构抗震性能,避免引起结构发生连续性倒塌的失效模式.
笔者通过钢筋混凝土柱振动台试验对 LSDYNA有限元程序[7]中的纤维单元模拟构件动力响应过程的可靠性进行验证,进而对一个4层钢筋混凝土框架结构进行强震作用下动力弹塑性分析,采用基于能量阈值的损伤准则对框架柱进行损伤分析,再由构件损伤指数加权组合得到结构整体损伤指数,从而实现强震作用下结构失效过程的定量分析.
1 损伤准则
1.1 构件的损伤准则
构件损伤指数定义为能量阈值和滞回耗能的线性组合,通过耦合系数考虑两者相互影响、权重系数考虑两者对损伤贡献的大小,因此构件的损伤准则定义为

式中:di为构件在第 i时间步的损伤程度;r,ie、iE分别为单步能量阈值和总滞回耗能;ue、uE分别为构件破坏点的能量阈值和滞回耗能;β为考虑损伤能量阈值与滞回耗能对构件损伤贡献的权重系数;ψ为归一化系数;αE、αe分别为考虑能量阈值与滞回耗能的耦合系数,即

式中cE和ce分别为考虑滞回耗能与损伤能量阈值相互影响的临界值.各参数的确定过程参见文献[8].
1.2 结构整体的损伤准则
结构整体损伤准则[5]定义为

式中:di为第i个构件的损伤指数;Ei为第i个构件损伤的权重系数,定义为相应构件滞回耗能总和.
2 钢筋混凝土柱的损伤分析
2.1 分析模型及模型参数
为验证 LS-DYNA有限元程序[7]中纤维单元模型的计算精度和计算成本,对文献[9]所述受双向地震作用的正方形截面钢筋混凝土柱进行动力弹塑性时程分析,柱横截面尺寸为 600,mm×600,mm,保护层厚度40,mm,箍筋直径6,mm,间距75,mm,纵筋直径 10,mm,配筋率为 0.95%.柱有效长度为 3.0,m,在柱顶附加质量模拟上部结构重力荷载,附加质量为34,t,如图 1所示.数值模拟中,柱沿轴向离散成 10个梁单元,每个单元长度为 0.2,m,小于柱脚塑性铰[10]长度 0.47,m;梁单元横截面离散成 225个混凝土纤维和 48个钢筋纤维,不考虑混凝土和钢筋之间的黏结滑移,并且纤维之间变形符合平截面假定.柱离散过程如图 1所示,图中加深部分为核心区混凝土.柱顶配重采用刚性梁单元模拟,配重质心高度为3.0,m;柱底理想固结,沿x、y两个方向输入按1/2压缩后的Kobe地震波.
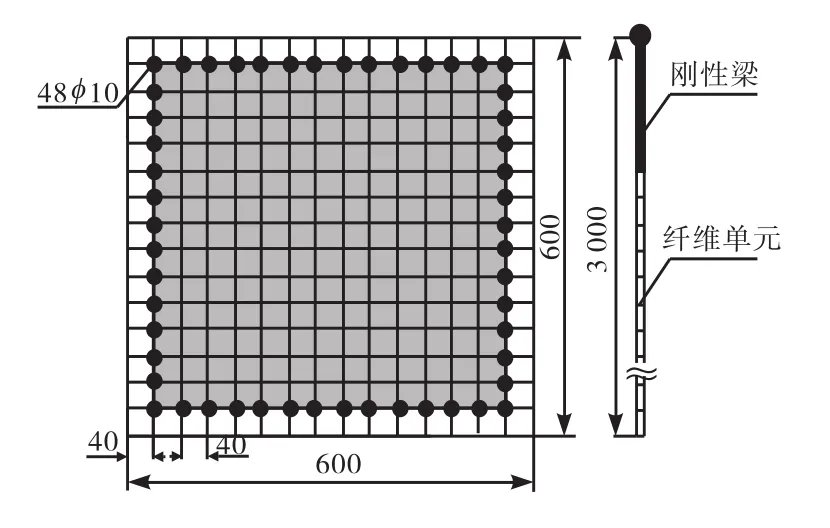
图1 钢筋混凝土柱离散Fig.1 Discrete of RC column
钢筋采用单轴弹塑性流动强化本构模型,屈服应力和弹性模量采用实测值,通过 Ramberg-Osgood方程[9]模拟材料反复加载时刚度退化.混凝土采用Kent-Park本构模型[11],混凝土轴心抗压强度和弹性模量采用实测值,考虑箍筋对混凝土的约束作用,核心区混凝土本构关系[12]定义为
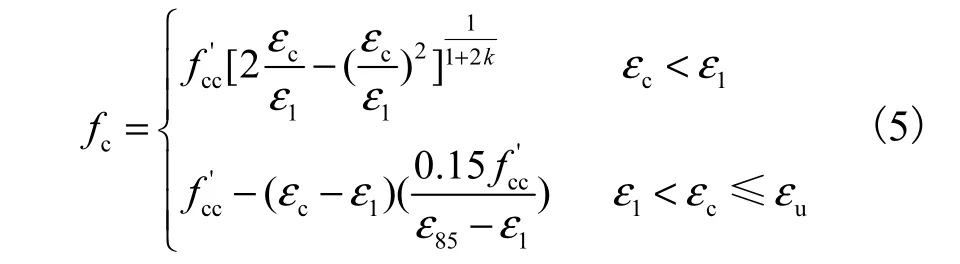


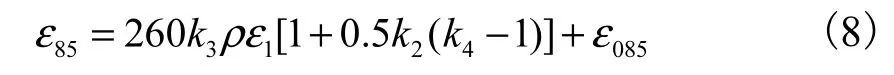
式中:f1e为等效横向约束力,k、k1、k2、k3和 k4分别为与构件截面形式、箍筋配置、未约束混凝土性能等有关的参数.数值模拟中,混凝土的本构关系如图 2所示,混凝土柱的材料参数如表1所示.
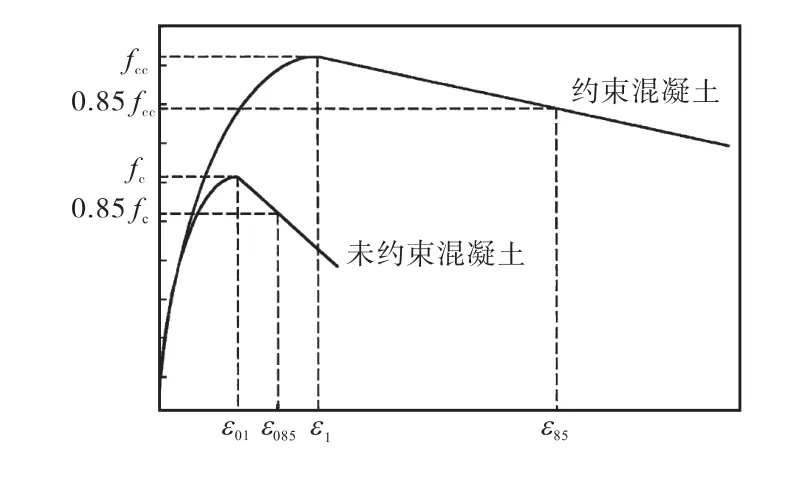
图2 混凝土应力应变关系Fig.2 Stress-strain relationship for concrete

表1 混凝土柱材料参数Tab.1 Material parameters of concrete column
2.2 结果分析
数值模拟采用与试验相同的采样频率,试验与数值模拟所得配重质心加速度时程曲线和位移时程曲线如图3~图6所示.
由图3~图6可以看出,纤维单元模型能很好地模拟双向地震作用下钢筋混凝土柱的动力弹塑性响应.在峰值响应阶段,数值模拟结果与试验结果基本吻合;峰值响应后,数值模拟得到的加速度和残余变形均较试验值偏大,其主要原因为:试验时振动台会对输入的地震动产生滤波效应,使作用在柱底的地震动与数值模拟中输入的理想 Kobe地震动有差异;试验过程中,随着部分混凝土压溃、钢筋屈服拉断,柱子的阻尼比会增大,数值模拟未考虑柱子破坏过程中阻尼比增大的影响;试验中钢筋与混凝土存在黏结滑移效应,数值模拟对此考虑欠佳;试验时,柱子采用螺栓锚固到振动台台面上,柱子与振动台之间会产生变形,而数值模拟假定柱底与振动台理想固结.上述原因导致数值模拟的加速度和位移时程与试验结果在后部分产生误差,但总体拟合较好.

图3 x方向加速度时程Fig.3 Time history of acceleration in x direction
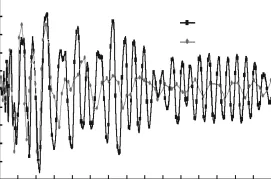
图4 y方向加速度时程Fig.4 Time history of acceleration in y direction
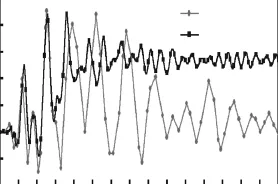
图5 x方向位移时程Fig.5 Time history of displacement in x direction

图6 y方向位移时程Fig.6 Time history of displacement in y direction
地震动输入结束后,继续向柱顶施加竖向荷载至柱子压溃以评估柱竖向剩余承载力,采用基于能量阈值的损伤准则模拟柱子竖向剩余承载力退化过程如图7所示.由图7可以看出,地震动加速度峰值期间(1~6,s)柱子损伤发展很快,7,s时刻柱子损伤指数约为 0.62,此后损伤缓慢发展,地震动输入结束时柱子尚有竖向剩余承载力,损伤指数约为0.79.

图7 损伤发展过程Fig.7 Damage evolution process
3 钢筋混凝土框架结构的失效分析
3.1 结构模型及模型参数
所分析结构为 4层钢筋混凝土框架结构,结构底层层高4.8,m,2~4层层高3.6,m,柱网横向5跨、间距7.5,m,纵向3跨、间距 6.0,m,如图 8所示.各层框架柱截面相同为600,mm×600,mm,梁柱采用C40混凝土、HRB335钢筋,纵筋直径 22,mm,配筋率约为1.404%,箍筋为φ 8@100,体积配箍率约为 0.74%;框架梁截面尺寸为700,mm×300,mm,梁端负弯矩区上部纵筋为4φ20,下部为 4φ18,中部设置4φ12构造钢筋,箍筋为φ8@100;楼板厚度100,mm,混凝土强度等级为 C30,下部钢筋为φ8@100,上部钢筋为φ10@125.填充墙等非受力构件按质量等效到楼板和柱子处,等效后楼面均布恒荷载约为6,kN/m2.
采用前述纤维单元模型模拟结构梁柱构件,柱截面离散为64根混凝土纤维和12根钢筋纤维,梁截面离散为50根混凝土纤维和12根钢筋纤维,梁柱沿轴向均离散成4个单元;考虑箍筋对柱核心区混凝土的约束作用,不考虑箍筋对梁的约束作用,混凝土材料参数如表 2所示.采用分层壳单元模型模拟楼板,楼板沿厚度离散成10个混凝土层和2个钢筋层.分析中假定结构柱脚理想固结于地面,基底施加 El-Centro双向水平地震激励,地震动加速度峰值调幅为8,m/s2,以模拟结构强非线性响应和失效过程.
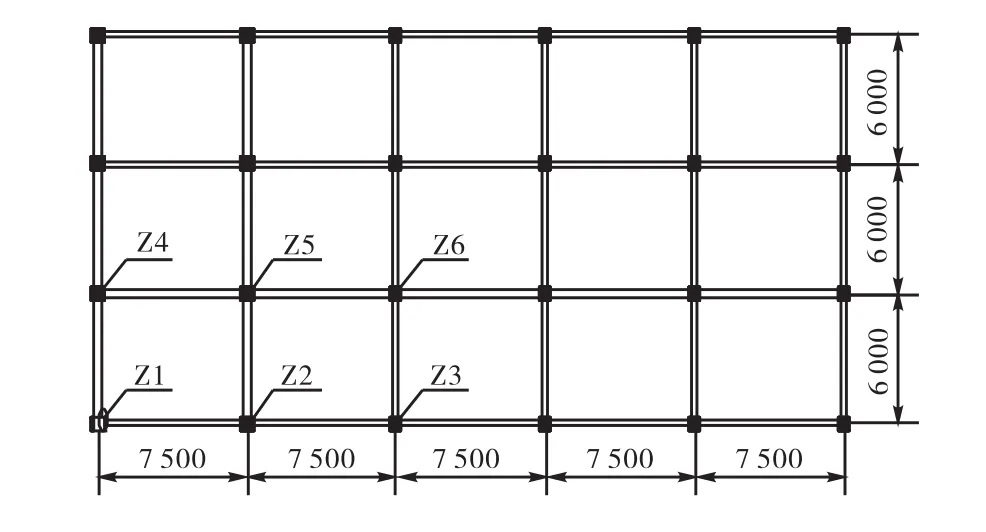
图8 结构平面示意Fig.8 Plan of structure
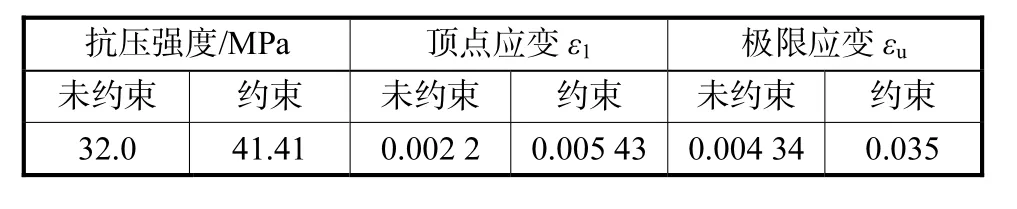
表2 混凝土框架材料参数Tab.2 Material parameters of concrete frame
3.2 结果分析
由于框架梁柱参数不沿楼层变化,层高最大的底层为结构薄弱层,只分析结构底层损伤发展过程.为简化分析,将底层柱按柱参数及边界条件分成6类,分析中认为同类柱损伤发展过程相同,柱子分类如图 8所示.图 9所示为结构底层各类柱子损伤发展过程,图10为底层整体损伤发展过程.
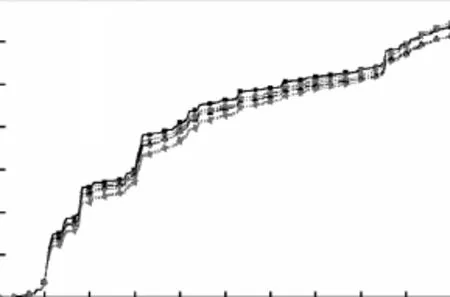
图9 柱子损伤发展过程Fig.9 Damage evolution process of columns
由图9可以看出,6类柱子损伤发展趋势相近.分析其原因为:所分析结构平立面规则,结构扭转效应小,柱子首次超越破坏可以近似以柱顶位移代替能量阈值,而结构楼板平面内刚度很大,各柱顶点位移几乎相等,所以具有相似的损伤发展过程.从图 9还可以看出,Z5和 Z6损伤发展过程基本重合,在大型结构分析中可粗略地将其分为一类;Z2~Z4损伤程度在Z1和Z6之间,即Z1和Z6分别具有最大和最小的损伤指数,主要原因是Z1的轴压比最小,柱子破坏点能量阈值较轴压比最大的Z6小,容易产生首次超越破坏,而Z6相对Z1更容易产生累积破坏[13-14],这与图9中Z1和Z6损伤指数的差值逐渐缩小相符合.
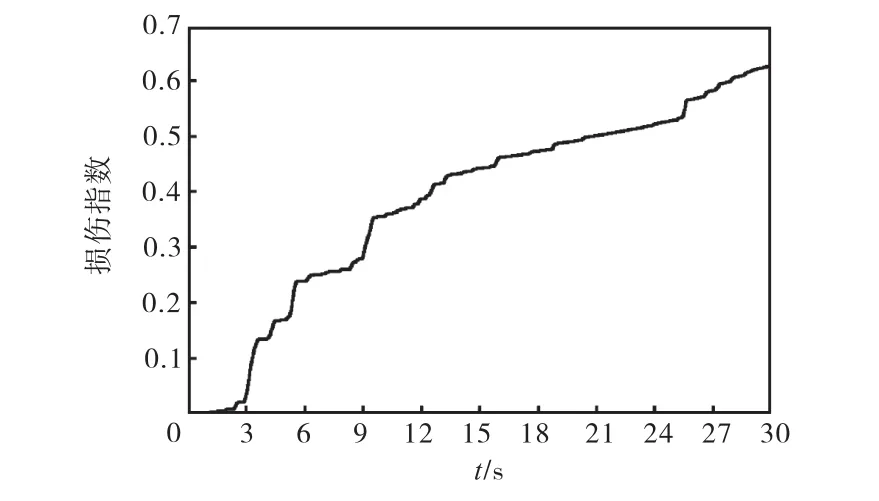
图10 底层损伤发展过程Fig.10 Damage evolution process of first story
由图 10可以看出,结构底层损伤发展趋势与单根柱子相同,在2.7,s和11.7,s时损伤迅速发展,这与El Centro地震动两个水平分量峰值加速度时刻相对应,此后损伤逐渐累积,地震动输入结束时结构损伤指数为0.62,结构尚未倒塌.
4 结 语
采用纤维单元模型对一个钢筋混凝土悬臂柱的振动台试验进行弹塑性验证分析,证明考虑箍筋对核心区混凝土的约束作用后,纤维单元模型能以很低的计算成本获得很高的计算精度,并能很好地模拟柱子竖向剩余承载力的退化过程.对一个 4层钢筋混凝土框架结构损伤分析表明,结构底层各类柱子损伤发展趋势相近,与轴压比较小的柱子相比,轴压比大的柱子总滞回耗能小、累积破坏更明显、结构延性相对较差,但首次超越破坏的阈值较大.结构薄弱层损伤发展过程与单个柱子损伤发展相似,表现为地震动峰值加速度时刻损伤迅速发展,其余时刻的结构薄弱层损伤指数缓慢增加.
[1] Sezen H,Whittaker A S,Elwood K J,et al. Performance of reinforced concrete buildings during the August 17,1999 Kocaeli,Turkey earthquake,and seismic design and construction practice in Turkey[J]. Engineering Structures,2002,25(1):103-114.
[2] Maqsood S T,Schwarz J. Analysis of building damage during the 8 October 2005 earthquake in Pakistan[J].Seismological Research Letters,2008,79(2):163-177.
[3] Spacone E,Filippou F C,Taucer F F. Fiber beamcolumn model for non-linear analysis of RC frames(Part I):Formulation[J]. Earthquake Engineering and Structural Dynamics,1996,25(7):711-725.
[4] Spacone E,Filippou F C,Taucer F F. Fiber beamcolumn model for non-linear analysis of RC frames(PartⅡ):Application[J]. Earthquake Engineering and Structural Dynamics,1996,25(7):727- 742.
[5] Williams M S,Sexsmith R G. Seismic damage indices for concrete structures:A state-of-the-art review[J].Earthquake Spectra,1995,11(2):319-349.
[6] Elenas A. Correlation between seismic acceleration parameters and overall structural damage indices of buildings[J]. Soil Dynamics and Earthquake Engineering,2000,20(1/2/3/4):93-100.
[7] LS-DYNA. Keyword User's Manual[M]. Livermore,California:Livermore Software Technology Corporation,2006.
[8] 吕 杨,徐龙河,李忠献,等. 钢筋混凝土柱基于能量阈值的损伤准则[J]. 工程力学,2011,28(5):84-89.Lü Yang,Xu Longhe,Li Zhongxian,et al. Energy threshold based damage criterion of reinforced concrete columns[J]. Engineering Mechanics,2011,28(5):84-89(in Chinese).
[9] Hideaki N,Shigeki U. Dynamic response characteristic of reinforced concrete column subjected to bilateral earthquake ground motions[C]// 13th World Conference on Earthquake Engineering. Vancouver,Canada,2004:576.
[10] Lehman D E,Moehle J P. Seismic Performance of Wellconfined Concrete Dridge Columns[R]. Berkeley:University of California,Pacific Earthquake Engineering Research Center,1998.
[11] Kent D C,Park R. Cyclic load behaviour of reinforcing steel[J]. Strain,1972,9(3):98-103.
[12] Kent D C,Park R. Flexural members with confined concrete[J]. Journal of the Structural Division,1971,97(7):1969-1990.
[13] Yalcin C,Saatcioglu M. Inelastic analysis of reinforced concrete columns[J]. Computers and Structures,2000,77(5):539-555.
[14] Haselton C B,Deierlein G G. Assessing Seismic Collapse Safety of Modern Reinforced Concrete Moment-Frame Buildings[R]. Berkeley:University of California,Pacific Earthquake Engineering Research Center,2007.
