铝合金热变形的本构模型研究

黄长清，刁金鹏 ，邓华

(1. 中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083；2. 湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙，410082；3. 湖南大学 材料科学与工程学院，湖南 长沙，410082)

6×××铝合金是一种可热处理强化铝合金，此类合金具有良好的可成形性、抗蚀性、可焊性以及较强的疲劳强度与中等的静态强度，用于制造飞机油箱、油管，汽车、船舶等交通运输装备的钣金件、仪表、街灯支架、制泠装置、电视塔、钻设备、导弹零件、铆钉线材等[1-5]，它也是欧美全铝汽车覆盖件的首选材料。作为全铝汽车覆盖件用的铝合金，需要通过热轧和冷轧工艺来制成符合冲压成形要求的板材。在热轧或热变形过程中，材料的高温流变应力σ取决于变形温度T和应变速率ε&。通过引入Zener-Hollomon参数，将流变应力σ表达为参数Z的指数函数关系、幂函数关系和双曲函数关系，为用参数Z研究变形条件与材料组织和性能演变的关系提供方便[6-7]。然而，在上述描述热变形流变应力行为的函数关系中，材料常数通常认为与温度无关。实际上，在高温压缩变形实验中产生的变形热对真应力-真应变曲线也有一定影响，变形热能的存在会导致实际变形温度升高从而使材料出现软化现象[8]。因此，在铝合金热变形过程中，有必要考虑温升对流变应力的影响。许多学者[9-10]对作为高强材料的2×××，7×××和5×××系某些重要铝合金的流变行为和本构关系进行了研究，但对6×××系尤其是作为汽车覆盖件使用的铝合金材料的研究较少。在此，本文作者以6016铝合金为研究对象，采用高温单道次热压缩实验研究其热变形流变行为，并考虑变形过程中的温升对流变应力的影响，对真应力-真应变曲线进行修正，建立高精度的流变应力本构方程，以便为6016铝合金热轧和常规热加工工艺的制订提供理论指导。

1 实验

6016铝合金是一种Al-Mg-Si系铝合金,其主要合金元素为Mg和Si。实验用6016铝合金取自工业粗轧厚板，其化学成分如表1所示。为了获取成分均匀的试样，用线切割垂直板材割取直径×高度为 10 mm×15 mm的圆柱体试样，如图1所示。

表1 6016 铝合金的化学成分(质量分数)Table 1 Chemical compositions of 6016 aluminum alloy %

实验前，对试样在箱式电阻炉内进行均匀化处理：在 550 ℃保温 12 h后出炉水淬。压缩实验在Gleeble-1500热模拟机上进行，压缩试样装置如图2所示。在压缩之前，在圆柱试样两端的槽内填充75%(质量分数，下同)石墨+20%机油+5%硝酸三甲苯酯，以减小压缩时端面摩擦对应力状态的影响。试验温度为300～500 ℃，应变速率为0.1～10 s-1，总压缩应变(真应变)为0.8。利用试样自身电阻实现电加热，加热速度为10 ℃/s，变形前保温3 min，变形终了时立即水淬。

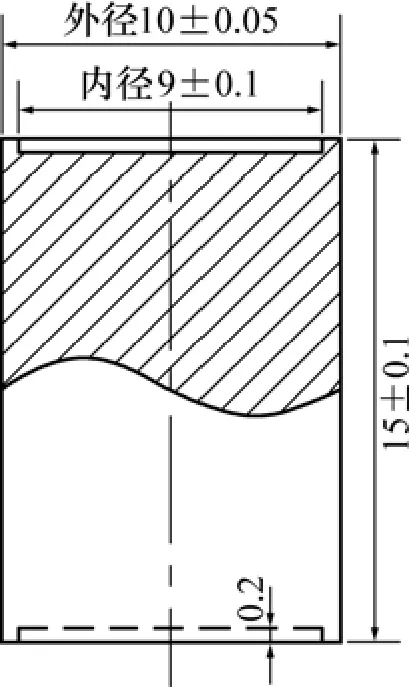
图1 压缩试样形状Fig.1 Shape of specimen

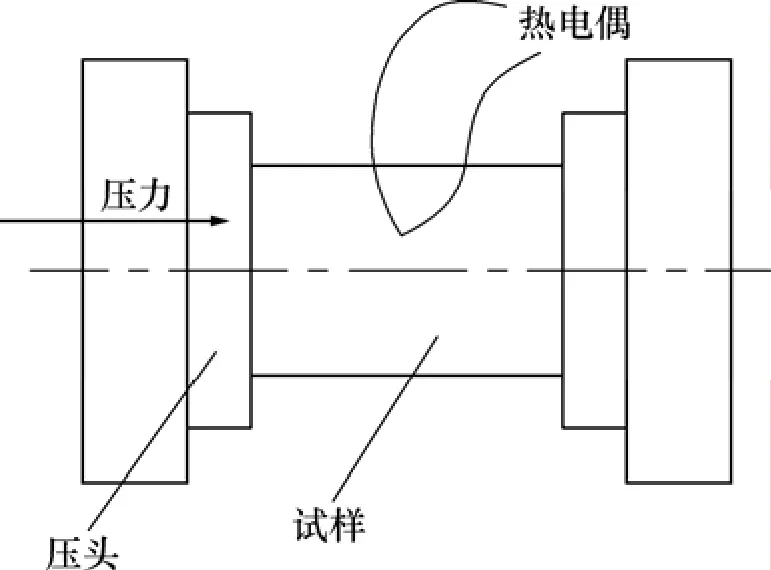
图2 压缩试样装置示意图Fig.2 Schematic of compressed samples device

2 结果与讨论

2.1 流变曲线的温升修正

在铝合金变形过程中，机械能大部分转化为变形热能，小部分储存于位错、空位等缺陷中。变形热能的存在会导致实际变形温度升高，从而影响其真应力-应变曲线。在低应变速率下，大部分变形热通过夹具散失到外界环境中，产生的温升可以忽略；而在高速率条件下，不仅产生较大的热量，而且变形热能来不及散失，使铝合金温度升高[11]。为了保证流变应力方程的准确性，有必要对高速率变形下的试样温度进行理论计算。

变形热对温度的影响可根据下式计算[12]：

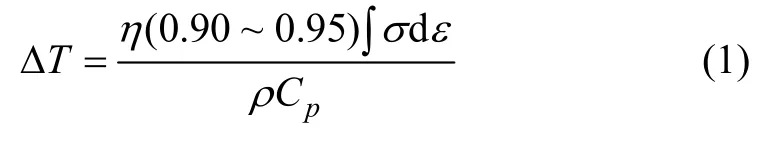
式中：ΔT为温度差；∫σdε为机械能；ρ为实验材料的密度，ρ=2.7 t/m3；Cp为实验材料的比热容，Cp=896 J/(kgK)；0.90～0.95为机械能转化为变形热的比例；η为绝热因子，是保留在试样内的热与总变形热的比值，其表达式为：

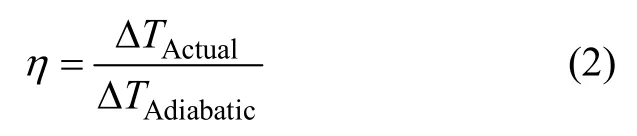
η介于0～1之间，在等温低应变速率变形条件下，其值为0；而在高应变速率绝热的条件下，其值取1。热模拟压缩试验条件近似于高应变速率绝热，本文中η取1。

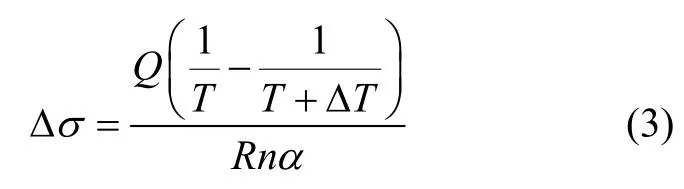
根据Devadas等研究[13]，温升对流变应力的影响可由下式描述：式中：Q为热变形激活能，它反映材料热变形的难易程度，是材料在热变形过程中重要的力学性能参数；R为摩尔气体常数，8.31 J/(molK)；T为热力学温度；ΔT为温升；n和α为描述材料高温流变特性的重要参数，在这里分别取8.525 4和0.018 3。通过式(1)～(3)对真应力-真应变曲线进行修正。

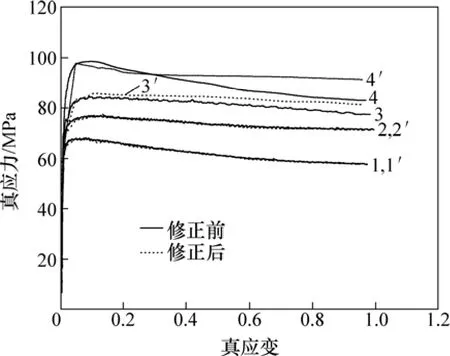
图3 400 ℃时6016 铝合金修正前、后的真应力-真应变曲线对比Fig.3 Comparison between corrected and uncorrected true stress-true strain curves for 6016 aluminum alloy at 400 ℃

图3所示是变形温度为 400 ℃、应变速率为0.01～10 s-1时流变应力修正前、后的对比情况。从图3可以看出：随应变速率增大，温升引起的应力变化也逐渐增大；当应变速率为10 s-1时，温度升高27.9℃，造成流变应力下降，应力修正值比实测值高11.1%左右；修正之后的流变应力先随应变的增大而迅速升高，达到峰值后逐渐下降，出现不同程度的软化现象，这是此时金属发生了动态再结晶所致。

2.2 实验结果

图4所示为6016铝合金在不同应变速率下的高温热压缩变形真应力-真应变关系曲线。

由图4可以看出：6016铝合金高温热压缩变形可以分为应变硬化和稳态变形2个阶段。在变形的开始阶段，流变应力随应变增加而迅速升高，显示出明显的加工硬化现象。这是由于在外加应力的作用下，位错密度急剧增加，导致位错之间相互交割缠结，位错运动难以进行；同时，由于应变较小，晶内储存能较少，动态回复和动态再结晶等软化过程难以进行，此时，加工硬化处于主导地位，故应力水平迅速上升。随着应变不断增大，晶内的储存能逐渐升高，动态软化与加工硬化逐步趋向平衡，此时变形过程进入稳态变形阶段；随着应变增加，真应力基本不变。

由图4还可见：该合金流变应力受变形温度和应变速率的影响较大。在同一应变速率下，随着温度的升高，真应力明显下降。这是因为温度升高后位错运动的阻力下降，空位、间隙原子等点缺陷的运动也更加活跃；在同一变形温度下，随着变形速率的增加，应力水平升高，这说明6016铝合金对应变速率敏感。

2.3 本构模型的建立

材料的高温变形特性可以用材料的流变应力方程来描述。经典的模型主要有Zuzin和Browman模型、Zener-Hollmon参数模型、Slater关系模型等。本文主要采用参数Z模型。

对于不同材料高温塑性变形，低应力下流变应力和应变速率之间的关系可以用指数关系描述[14-15]：

高应力下流变应力和应变速率之间的关系可以用幂函数关系描述：

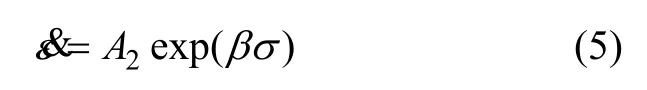
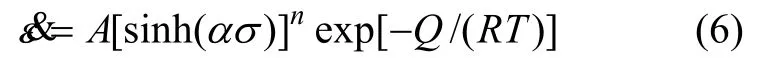
其中：A，α和n分别为与温度无关的常数。变形激活能Q反映了高温塑性变形过程中应变硬化和动态软化过程之间的平衡关系。

式中：A1，A2和β分别为与温度无关的常数。考虑到高温蠕变存在热激活过程，Jonas等[14-15]综合式(5)提出了一种包含变形激活能Q和温度T的双曲正弦函数形式，并引入Arrhenius关系，来描述热激活行为：

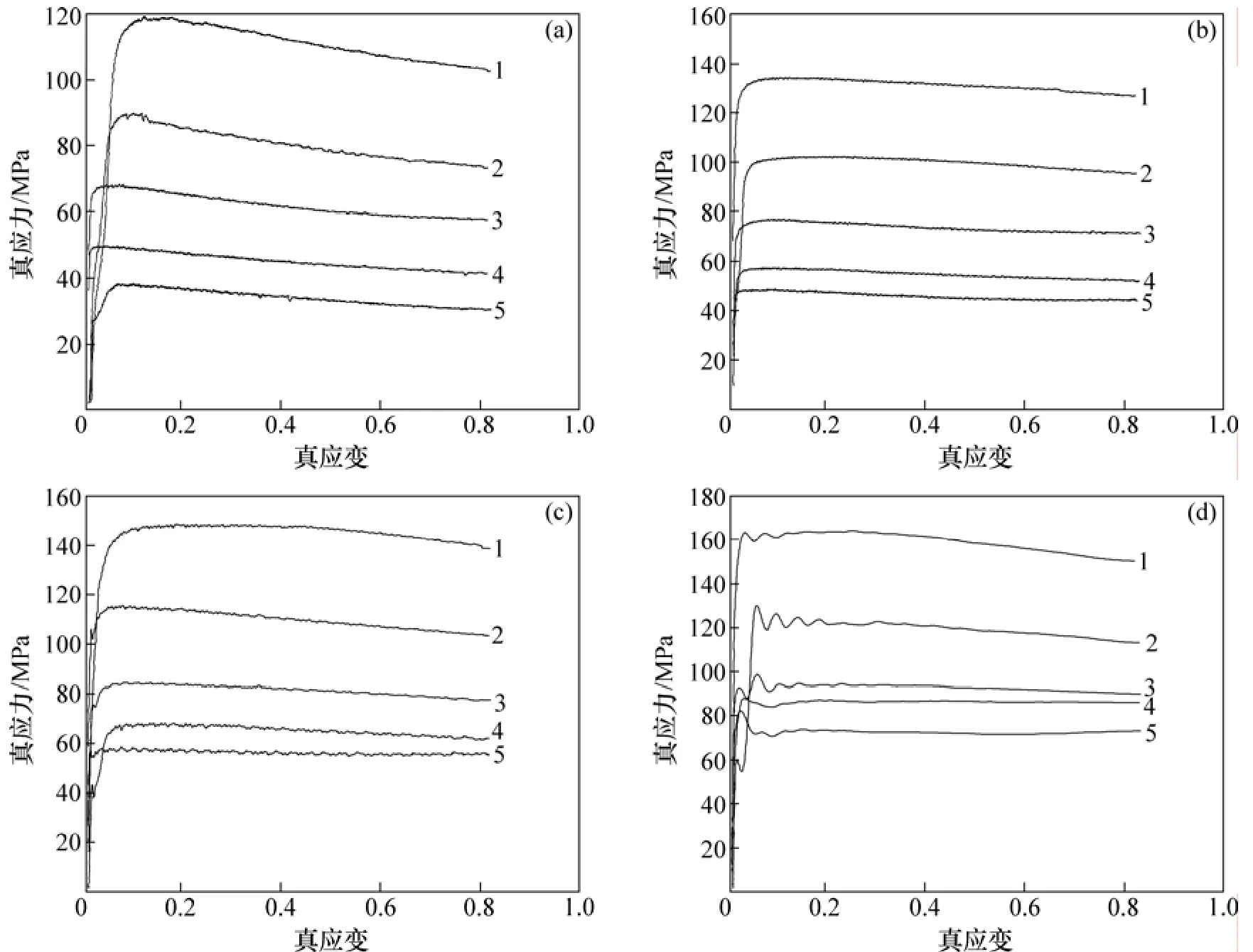
图4 6016铝合金在不同应变速率下的高温压缩变形真应力-真应变曲线Fig.4 True stress-true strain curves of 6016 aluminum alloy by high temperature single-pass compression experiment at different strain rates

α，β和n之间存在如下关系：

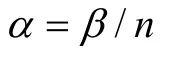
为了能描述较宽温度范围内流变应力和应变速率的关系，Zener-Hollmon等提出了温度补偿应变速率[16]，即Zener-Hollmon参数Z的概念，其表达式为：

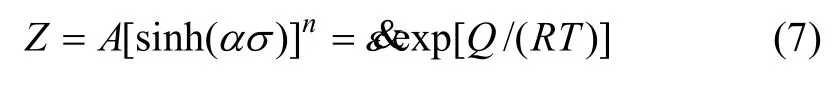
由式(7)可以推出：

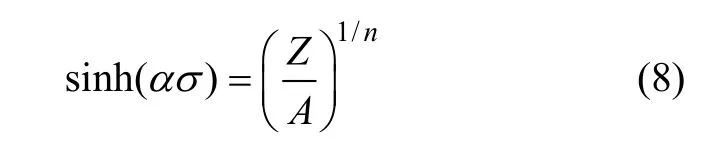
分别对式(4)和(5)两边取自然对数，可以得到：

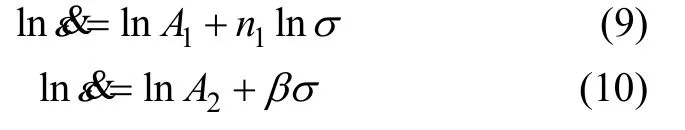
将经过温升修正之后的不同变形温度条件下6016铝合金的峰值应力随应变速率变化情况分别代入式(9)和(10)，绘制出 lnε&-lnσ和 lnε&-σ的关系曲线。6016铝合金应变速率与流变应力之间的关系如图5所示。用数学软件对式(9)和(10)进行一元线性回归处理。

由式(9)和(10)可知：当温度一定时，n1和β分别为lnε&-lnσ和lnε&-σ曲线的斜率；n1为图5(a)中温度为400，450和500 ℃时3条直线斜率的平均值，得n1=13.043 3；β为图5(b)中温度为300和350 ℃时2条直线斜率的平均值，得β=0.185 2 MPa-1，则α=β/n1=0.014 2 MPa-1。

假设变形激活能Q与变形温度无关，对式(6)两边取对数，整理得：

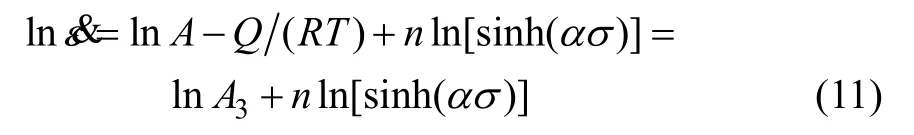
由式(11)可知：

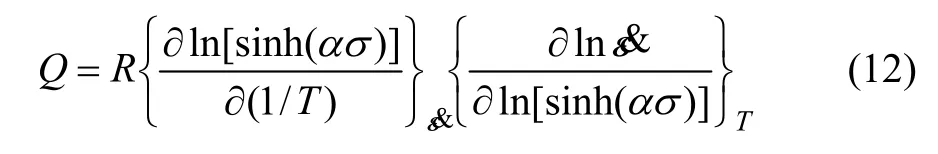
根据式(12)，取σ为峰值应力，将图3 中不同温度下6016铝合金变形时的峰值应力、应变速率和所求的α代入式(11)，用数学软件进行线性回归处理，绘制出相应的lnε&- ln[sinh(ασ)]关系曲线，如图6 所示；ln[sinh(ασ)]-1/T关系曲线如图7所示。n和Q/(Rn)分别为 lnε&-ln[sinh(ασ)]和 ln[sinh(ασ)]-1/T曲线的斜率，由此可求得变形激活能Q以及应力指数n，分别为：Q=270.257 kJ/mol，n=8.525 4。6016铝合金的应变激活能Q比纯铝的自扩散激活能要大，这是 Mg和 Si等原子的溶入产生了强化所致。

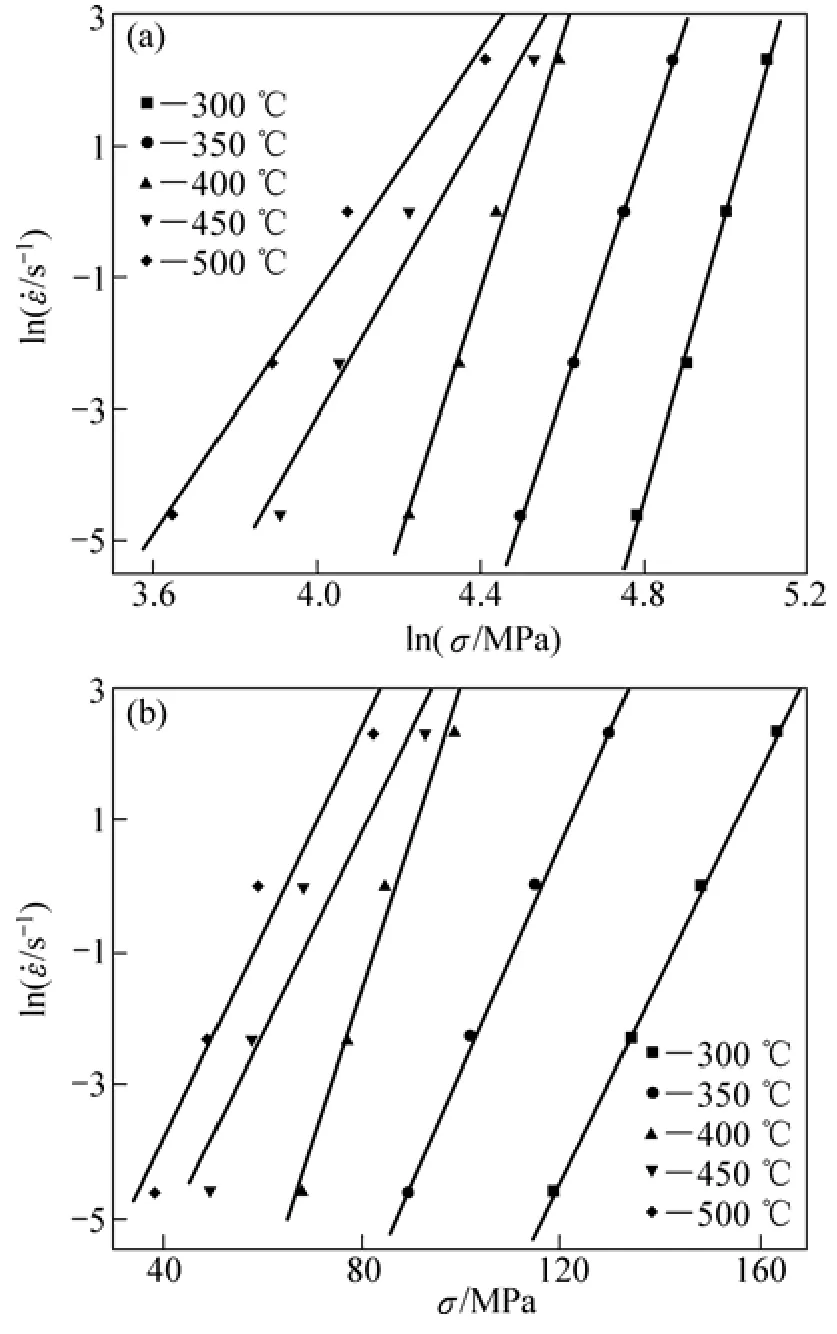
图5 不同变形温度下应变速率与流变应力之间的关系Fig.5 Relationships between strain rate and flow stress at different temperatures

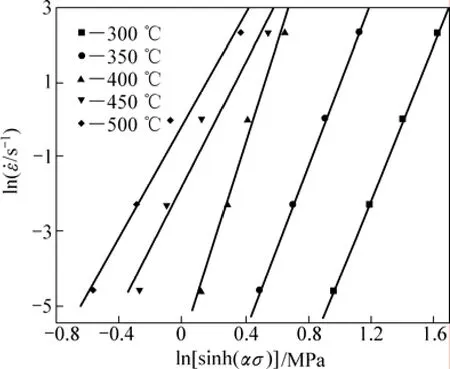
图6 不同温度下 lnε&-ln[sinh(ασ)]的关系Fig.6 Relationships between lnε&and ln[sinh(ασ)]at different temperatures

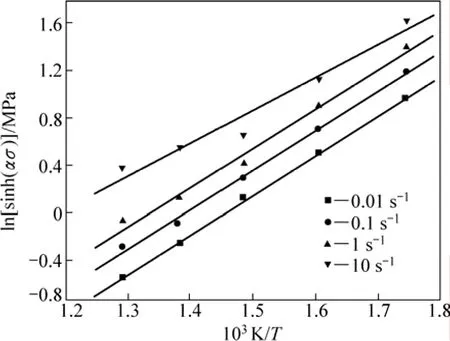
图7 不同温度下ln[sinh(ασ)]-1/T的关系Fig.7 Relationships between ln[sinh(ασ)]and 1/T at different temperatures

由图6 可知：lnε&和 ln[sinh(ασ)]较好地满足线性关系，即6016铝合金高温压缩变形时的应力-应变速率满足双曲正弦函数关系，可用双曲正弦函数关系描述该合金整个应力水平下的流动应力和应变速率之间的关系，为通过控制应变速率来控制热加工的应力水平和力学性能的加工工艺制定提供了理论依据。由图7可知：ln[sinh(ασ)]和 1/T较好地符合线性关系，从而证实了 6016铝合金高温变形时应力和变形温度之间的关系属于Arrhenius 关系，即可用包含Arrhenius项的Z参数模型描述高温压缩变形时的流变应力行为。

对式(7)两边取对数可以得到：

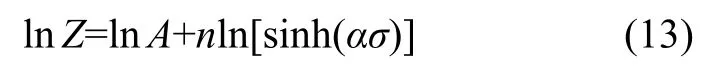
用数学软件作线性回归处理，得lnZ-ln[sinh(ασ)]关系曲线，如图8所示。

显然，6016铝合金lnZ和ln[sinh(ασ)]之间满足线性关系。求取该直线的截距为lnA=40.108，则材料常数A为2.62×1017s-1。根据式(7)以及反双曲正弦函数的定义，可将流变应力表达为Zener-Hollomon 参数Z的函数，并将以上所求的α，A和n代入得：

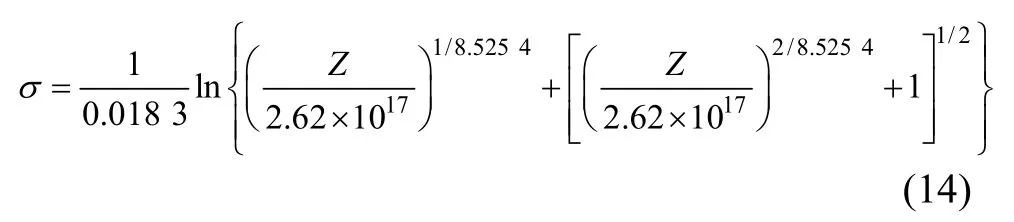
式中：

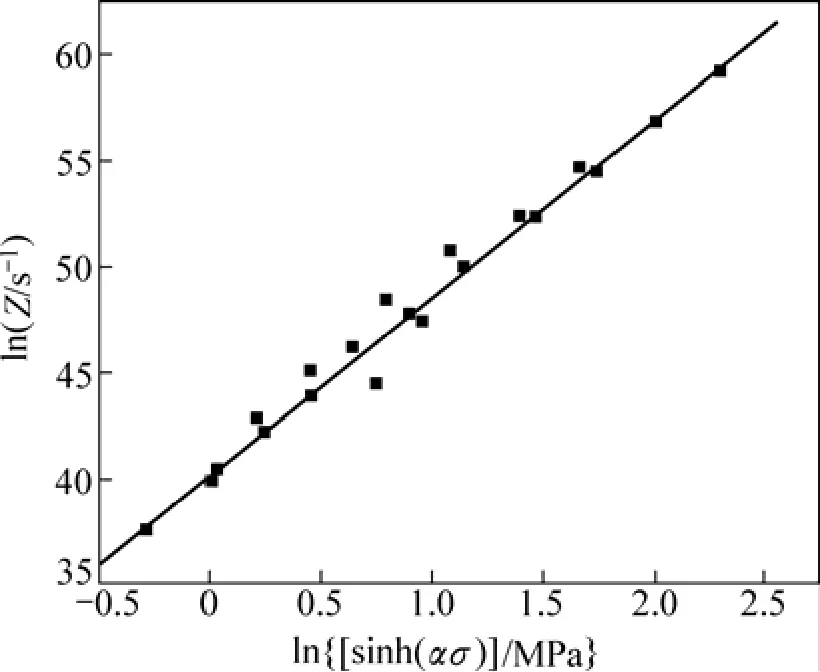
图8 ln Z-ln[sinh(ασ)]的关系Fig.8 Relationship between ln Z and ln[sinh(ασ)]

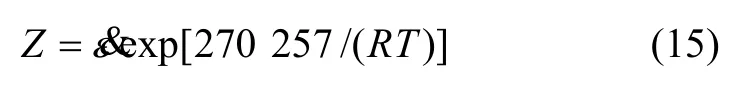
2.4 本构模型的验证

为了检验上述流变应力本构方程的精度，将应变速率为1 s-1，温度为300～500 ℃时6016铝合金等温变形时经温升修正的真应力-真应变曲线的实测值与预测值进行对比，如图9所示。

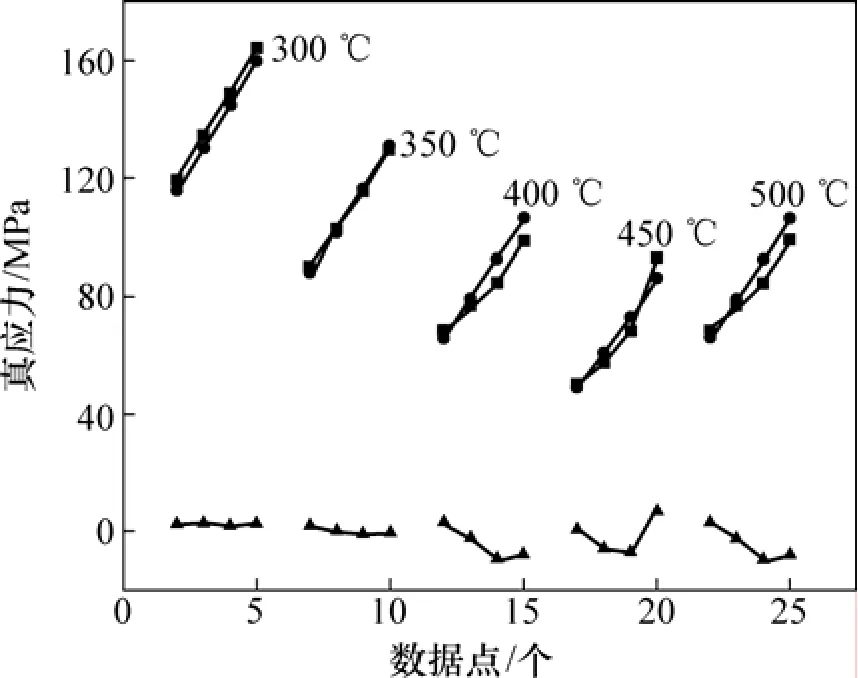
图9 应变速率1 s-1时流变应力预测值与实验值对比Fig.9 Comparison between predicted and experimental flow stress at 1 s-1 strain rate

从图9可以看出：流变应力的预测值与经温升修正的热模拟物理实验值较吻合，总体上误差较小；低温状态下误差很小，而高温变形时误差增大。这是由于本文的本构方程是以高应力变形状态为基础；而高温时流变应力较低，因而导致误差增大。

3 结论

(1) 6016 铝合金高温单道次压缩下的流变应力从应变硬化阶段过渡到稳态变形阶段，高温软化机制主要是动态回复。

(2) 当变形温度为300～500 ℃，应变速率为0.1～10 s-1时，在同一应变速率下，6016铝合金的流变应力和峰值应变随温度的升高而降低；在同一温度下，合金的流变应力和峰值应变随应变速率的增大而提高，说明该合金是正应变速率敏感材料。

(3) 采用Zener-Hollomon 参数的双曲正弦函数描述6016 铝合金高温流变应力σ，流变应力方程为：

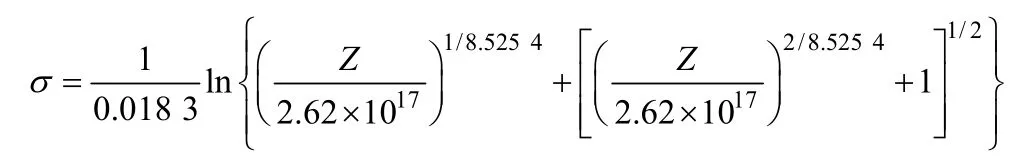
式中：Z=ε&e x p[270 257/(RT)]。

运用流变应力本构方程对不同应变速率、变形温度及应变条件下6016铝合金的流变应力进行预测，流变应力预测值与实验值较吻合。

[1]Spigarelli S,Evangelista E,McQueen H J. Study of hot workability of a heat treated AA6082 aluminum alloy[J]. Scripta Materialia,2003,49(2): 179-183.

[2]Garrett R P,Lin J,Dean T A. An investigation of the effects of solution heat treatment on mechanical properties for AA 6××× alloys: Experimentation and modeling[J]. International Journal of Plasticity,2005,21(8): 1640-1657.

[3]Claes F,Folon M. Casting,rolling and drawing 6201 alloy for overhead conductor[J]. Wire Journal International,1983,16(12):64-69.

[4]Dawson J R. Manufacture of all aluminum alloy conductors[J].Wire Journal International,1991,24(4): 37-40.

[5]Chia E H,McQueen H J. Microstructural control in aluminum alloys: Deformation,recovery and recrystallization[C]//Proceedings of a symposium at 1985 Annual Meeting of TMS.Warrendale,PA: The Metallurgical Society of AIME,1986:1-18.

[6]Cerri E,Evangelista E,McQueen H J. Overview of the high temperature substructure development in Al-Mg alloys[J]. High Temperature Materials and Processes,1999,18(4): 227-240.

[7]Gronostajski Z. The constitutive equations for FEM analysis[J].Journal of Materials Processing Technology,2000,106(1/2/3):40-44.

[8]林启权,彭大暑,张辉,等. 2519铝合金热压缩变形过程的动态与静态软化行为[J]. 中南大学学报: 自然科学版,2005,36(2): 183-l87.LIN Qi-quan,PENG Da-shu,ZHANG Hui,et a1. Dynamic and static softening behaviors of 2519 aluminum alloy during multi-stage hot compression deformation[J]. Journal of Central South University: Science and Technology,2005,36(2):183-187.

[9]李慧中,张新明,陈明安,等. 2519 铝合金热变形流变行为[J]. 中国有色金属学报,2005,15(4): 621-625.LI Hui-zhong,ZHANG Xin-ming,CHEN Ming-an,et al. Hot deformation behavior of 2519 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals,2005,15(4): 621-625.

[10]王孟君,任杰,黄电源,等. 汽车用 5182铝合金板材的温拉伸流变行为[J]. 中国有色金属学报,2008,18(11): 1958-1963.WANG Meng-jun,REN Jie,HUANG Dian-yuan,et al. Flow behavior of 5182 aluminum alloy for automotive body sheet during warn tensile deformation[J]. The Chinese Journal of Nonferrous Metals,2008,18(11): 1958-1963.

[11]潘清林,张小刚,李文斌,等. Al-Mg-Sc合金热压缩变形的流变应力行为[J]. 中南大学学报: 自然科学版,2009,40(4):926-931.PAN Qing-lin,ZHANG Xiao-gang,LI Wen-bin,et al. Flow stress behavior of Al-Mg-Sc alloy during hot compression[J].Journal of Central South University: Science and Technology,2009,40(4): 926-931.

[12]Baragar D L. The high temperature and high strain rate behavior of a plain carbon and an HSLA steel[J]. J Mech Work Technol,1987,14(3): 295-307.

[13]Devadas C,Baragar D,Ruddle G,et al. Thermal and metallurgical state of steel strip during hot rolling: Part II.Factors influencing rolling loads[J]. Metall Trans A,1991,22(2):321-333.

[14]Jonas J,Sellars C M,Tegart W J,et al. Strength and structure under hot working conditions[J]. Metallurgical Reviews,1969,14: 1-24.

[15]Shi H,Mclaren A J,Sellars C M,et al. Constitutive equations for high temperature flow stress of aluminum alloys[J]. Material Science and Technology,1997,13(3): 210-216.

[16]张辉,彭大暑,杨立斌,等. 铝合金多道次热轧流变应力的研究[J]. 热加工工艺,2000(5): 6-8.ZHANG Hui,PENG Da-shu,YANG Li-bin,et al. The study of flow stress for multipass hot-rolling of aluminum alloys[J].Metal Hotworking Technology,2000(5): 6-8.