填充式频谱共享中的功率分配算法分析

赵 刚,刘玉涛

(1.中国石油化工股份有限公司管道储运分公司通信处,江苏徐州221008;2.中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

在共享频谱接入中,多个认知用户可以同时接入同一条信道/载波,这时用户考虑来自其他用户的干扰[1,2]。根据授权用户的干扰容限约束,共享频谱接入策略下可以分为以下2种频谱接入模式：填充式(Overlay)频谱接入和下垫式(Underlay)频谱接入[3,4]。这2种接入策略直接影响频谱分配的方法,频谱资源的使用效率也不尽相同。

在下垫式频谱接入模式下,认知用户与授权用户共享频谱,需要考虑共用信道时所附加的干扰限制[5]。对于填充式频谱接入,认知用户伺机接入“频谱空穴”,它们只需要在授权用户出现时及时出让频谱而不存在与授权用户共享信道时的附加干扰问题,此种方法易于实现,且不需要现有通信设备提供干扰容限参数[6,7]。

1 系统模型

假设认知无线电网络中的N个认知用户可以以“机会主义”接入的形式共享授权用户的M条信道,N={1,…,N}与 M={1,…,M}分别表示认知用户及信道集合。授权用户的信道之间是相互正交的,且每条信道的带宽均为b=B/M。

当多个认知用户同时接入一条信道时,每个用户均把来自其他用户的信号当作噪声处理。

认知用户的信道增益可以表示为：

式中,βj表示用户对载波j的偏好参数,与载波的频率等有关;κ为用户天线在d0处的自由空间增益,且κ=λ/4π d0;d0与d分别表示天线远场的参考距离与认知用户收发机之间的距离;δ为路径损耗参数。

2 功率迭代算法

由于认知用户同时接入授权用户的空闲信道,接收机处的干扰除背景噪声外还有来自其他认知用户的干扰,这时,对任意的用户 i(i∈ N),其效用函数可以表示为：

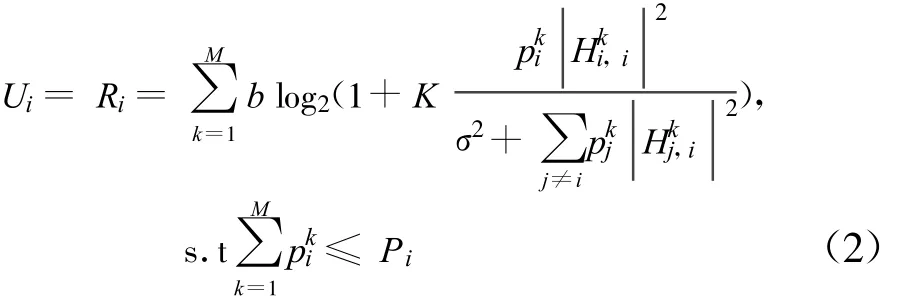
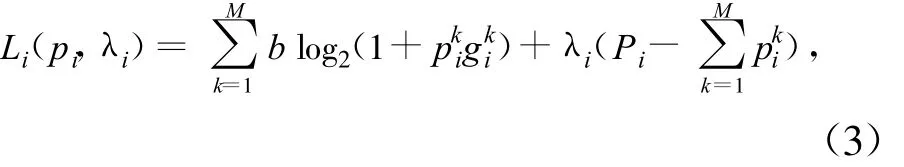
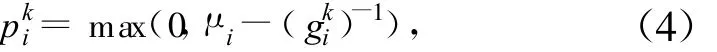
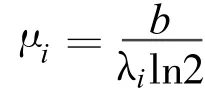
因此,可以得到如下所示的功率迭代方程：

由式(5)可知,对任意的用户 i(i∈ N),其第t+1阶段的功率分配策略与第t阶段其他所有用户的功率分配结果有关,即前一阶段的博弈结果会影响下一阶段的用户决策。尽管如此,用户的策略空间是各自独立的,在不超过其功率容限的前提下各个用户可以独立选取自身的功率分配向量;由于用户之间的自私、理性,他们均会按照式(5)选取最终的传输功率,从而实现自身效用的最优化。

3 仿真结果分析

下面,通过仿真来验证该迭代算法的收敛性与有效性。首先来分析N=2时的情形。假设授权用户工作在中心频率为1 GHz左右的非连续信道上,其可用信道总数M=10,b=20 kHz,不失一般性,假设第3、第7条信道处于工作状态。认知用户的总发射功率为P1=P2=10 mW,其收发机之间的距离分别为d1=1 000 m,d2=800 m,误码率水平 BER=10-4。取d0=100 m,δ=3,且假设用户 i的发射机到用户j的接收机的距离远大于d1与d2。

图1所示为认知用户1和用户2的功率分配结果。由图可知,对用户1而言,在传输功率的约束下,为优化自身的效用,并未选取状态较差的信道1进行数据的传输;对用户2而言,其收发机间的距离较小,相应的信道增益也较高,所以它在全部可用信道上均分配了适当的传输功率,特别的,由于信道1上受到的干扰较小(没有来自用户1的干扰信号),因此在该信道上分配了较多的功率。

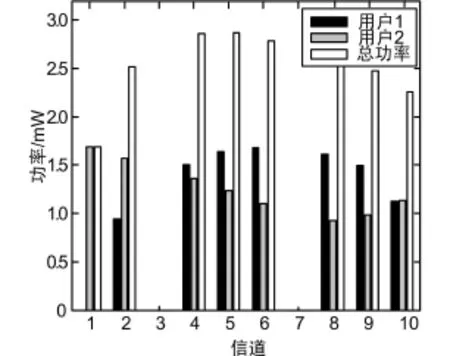
图1 功率分配结果(N=2)

图2所示为信道2、信道6和信道10上的功率分配结果随迭代次数的变化。由图可知,当迭代4次后功率即处于稳定状态,这说明该功率迭代算法的收敛速度很快。当用户i的发射机到用户j的接收机之间的距离与d1或 d2相当时,这里假设为1 500 m,经过仿真可得图3。由图可知,当与相当时,来自其他用户的干扰会很大,此时,为避免干扰造成的传输速率的降低,一般情况下每条信道只分配给单个认知用户使用。

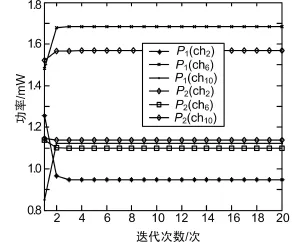
图2 功率迭代结果(N=2)

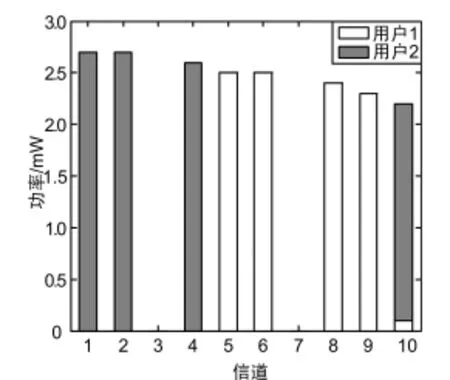
图3 功率分配结果(H2ij与H2ii相当)

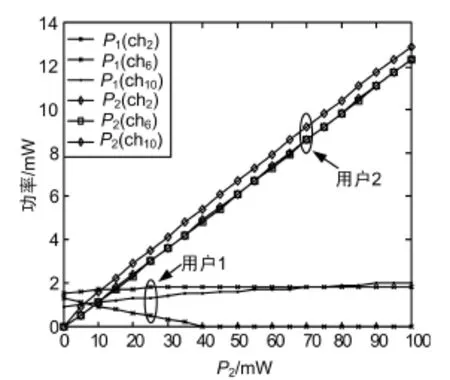
图4 功率分配结果与P2的关系

如图4所示为 P1=10mW时,信道2、信道6和信道10上的功率分配情况随P2的变化情况。随着P2的增加,这3条信道上承载的用户2的发射功率也逐渐增加,而用户1的功率变化不大(信道6与信道10)或逐渐降低到0 mW(信道2)。由图可知,当用户2在信道2上的发射功率超过5 mW时,用户1在该信道上的干扰功率较高,这时它将不再选用该信道进行通信。

当N＞2时,可以采用同样的方法进行分析。假设N=4,且 P1=P2=P3=P4=10mW,认知用户收发机间的距离分别为 d1=1 200 m,d2=800 m,d3=1 200 m,d4=600 m。如图5所示为信道2、信道6和信道10上的功率分配结果随迭代次数的变化情况。由图可知,当参与分配的认知用户数较多时,算法趋于稳定所需要的迭代次数也略有增加,但整体而言,该迭代算法具有较快的收敛性。

图5 功率迭代结果(N=4)

4 结束语

在基于overlay的频谱共享中,认知用户同时接入“频谱空穴”,此时的载波及功率分配问题可以通过多用户-多注水线算法来解决。主要研究了认知无线电中Overlay接入下的频谱分配问题,在注水原理的基础上提出了认知用户间功率分配的迭代算法,实现了用户间载波的合理及快速分配。研究的下一步将主要针对多用户下垫式频谱共享情况下的功率分配问题进行研究。

[1]DEVROYEN,MITRAN P,TAROKH V.Achievable rates in cognitiveradio channels[J].IEEE Transactions on Information Theory.2006 52(5)：1813-1827

[2]Kkolodzy P J.Interference temperature：A metric for dynamic spectrum utilization[J].International Journal of Network Management,2006,16(2)：103-113.

[3]YAOH,ZHOU Z,LIU H,et al.Optimal power allocation in joint spectrum underlay and overlay cognitive radio networks[C]∥2009 4th International Conference on Cognitive Radio Oriented Wireless Networks and Communications,CROWNCOM 2009.Hanover,IEEE CS,2009：1-5.

[4]SRINIVASA S,JAFAR S A.How much spectrum sharing is optimal in cognitive radio networks[J].IEEE Transactions on Wireless Communications,2008,7(10)：4010-4018.

[5]LE L,HOSSAIN E.Resource allocation for spectrum underlay in cognitive radio networks[J].IEEE Transactions on Wireless Communications,2008,7(12)：5306-5315.

[6]NIYATO D,HOSSAIN E.Competitive spectrum sharing in cognitive radio networks：A dynamic game spproach[J].IEEE Transactions on Wireless Communications,2008,7(7)：2651-2660.

[7]HAMDAOUI B.Adaptive spectrum assessment for opportunistic access in cognitive radio networks[J].IEEE T ransactions on Wireless Communications,2009,8(2)：922-930.