散射通信中的信噪比估计算法研究
2011-07-31毛晶晶陈小溪秦建存
毛晶晶,陈小溪,秦建存
(中国电子科技集团公司第五十四研究所,河北石家庄050081)
0 引言
信噪比(SNR)是信号强度和背景噪声的比值,是表征信道特性的重要参数。在通信系统的实际应用中,调制信号的识别、Turbo Code的迭代译码、功率控制、自适应调制切换以及自适应越区切换等功能都需要准确的信噪比估计[1]。在散射通信系统中,为了实现弹性通信,需要对信道状况进行实时的探测与估计,从而进行速率的变更,所以选择适用于散射信道的信噪比估计算法,对提升散射通信性能具有很大意义。
信噪比估计可以分为基于训练序列的估计和盲估计。盲估计法不需要引入导频信息,不影响信道传输效率,所以该文主要研究信噪比盲估计算法。目前对高斯白噪声(AWGN)信道下的盲信噪比估计已经有了不少方法。如最大似然估计算法、平方信噪比差估计(SNV)估计法、二阶四阶矩(M2M4)估计法、分离符号矩(SSME)估计法以及信号—方差比(SVR)估计法等[2,3]。下面主要针对中低速率散射通信信噪比估计的要求,仿真比较几种较实用的信噪比估计算法的性能。
1 散射通信系统结构
对流层散射信道的理想化短期模型可以看成是一种统计上平稳的独立衰落的许多路径的连续集,而每条路径呈现复高斯起伏。也就是说,对流层散射信道的短期模型可理想化为一广义平稳不相关(WSUSS)复高斯散射信道。
图1为对流层散射系统方框图(双天线站型)。在对流层散射通信中,一般均可采用分集技术、时间保护加失真自适应技术以及自适应均衡等抗多径技术来对抗信道的快衰落。
在弹性散射通信系统中SNR估计主要用于确定速率切换,所需要估计的参量为合路信噪比。大量的实验表明,采用上述抗多径措施后,散射信道的短期模型可以近似看成AWGN信道。

图1 对流层散射系统方框图
2 信噪比估计算法
QPSK调制具有很好的性能,广泛地应用于散射通信中。下面主要介绍3种适用于QPSK调制信号的盲信噪比估计算法。
2.1 文献[5]中的估计算法
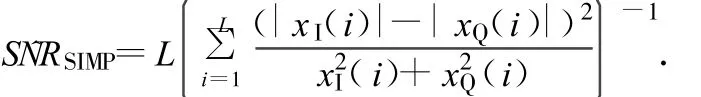
文献[5]中比较了4种针对QPSK调制的SNR估计算法的性能。其中估计量:具有最小的估计偏差以及最小的MSE,并且计算简单,比较适合实际应用。其中 xI、xQ分别为同相支路和正交支路的接收信号,L为数据长度。
2.2 最大似然估计改进算法
最大似然估计的基本算法是:假设噪声为零均值、方差 σ2未知的高斯白噪声,信号功率为 PS,根据噪声的概率密度函数求得接收信号的联合PDF。该方法旨在求解使得联合PDF最大的PS和 σ2的估计值,进一步得到SNR估计[3]。
考虑复信道条件下MPSK信号的ML估计。接收到的复数信号可以表示为:

式中 xI(n)、xQ(n)为接收信号的实部和虚部,sI(n)、sQ(n)为归一化的发送信号的实部和虚部。vI(n)、vQ(n)为归一化的零均值、方差为 σ2v/2的高斯噪声。Ps为信号功率,Pv为噪声功率,即噪声方差σ2v。进而可以得到单个接收信号的xI(n)和xQ(n)联合条件概率密度函数:

假定信号和噪声序列是相互独立的,由此可以得到L个接收信号的联合条件概率密度函数为:

对该联合条件概率密度函数取自然对数,就可以得到似然函数Γ(Ps),分别对 Ps和求偏微分,令其为0,即可分别得到 Ps和的最大似然估计,进而得到SNR的估计值:
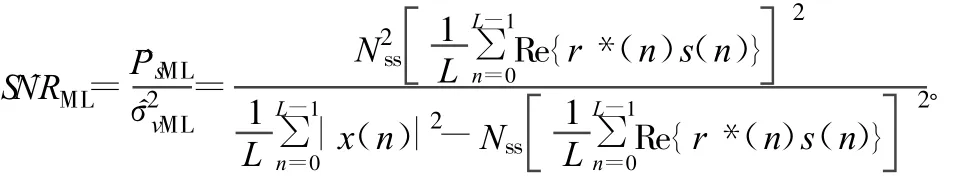
文献[4]给出了基于最大似然思想的一种信噪比估计的新算法,主要运用二次方去调制的方法,得到BPSK信号在复信道上的PˆsML估计,是一种非数据辅助方法。类推出针对QPSK的算法可表达为:
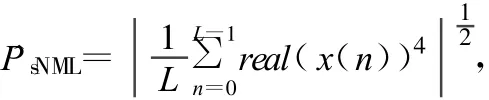
相应的SNR的估计算法为:

2.3 二阶四阶矩估计法
考虑在复信道条件下,假定信号和噪声都是零均值、相互独立的随机过程,且复噪声的同相分量和正交分量也相互独立。
接收信号序列可以表示为:

接收信号的二阶矩和四阶矩分别定义为:


式中,Ps是指信号功率指信号噪声方差,ks和kv分别是信号和噪声的kurtosis系数,为随调制方式和信道而变的常数。
对于复信道条件下的MPSK信号,ks=1,kv=2,所以得到:
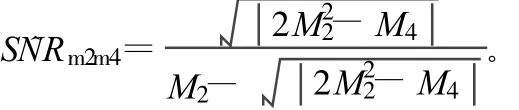
在实际应用中,二阶和四阶量是由接收序列的时间平均来计算的:
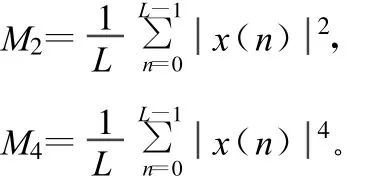
式中L为接收序列的长度。
3 仿真结果分析
假设信道为理想信道,对于调制信号这里考虑具有代表性的QPSK信号。选取仿真软件为Matlab。在信噪比0~20 dB范围上来比较3种算法的性能。
称文献[5]中的估计算法为算法1,最大似然算法的改进算法为算法2,M2M4算法为算法3。数据长度分别取200和1 000,得到图2和图3仿真结果。

图2 L=200算法性能比较图
从图2的仿真结果可以看出:3种算法在信噪比5~20 dB范围内性能都比较好,且随着L增大性能趋于完善。但是在较低信噪比(0~5 dB)时,算法1和算法2估计偏差较大,性能较差。算法3即使在低信噪比下也有比较好的性能。
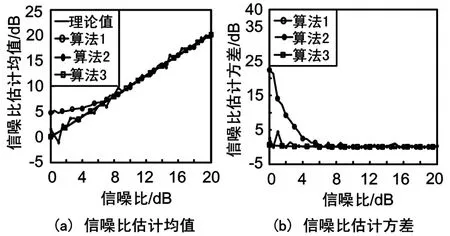
图3 L=1 000算法性能比较图
图3的仿真结果表明,随着信号数据观察长度L的增大,算法3的估计值越来越接近真实值,且估计标准差越来越小。该估计算法在整个信噪比估计范围中性能最为良好。
从运算复杂度来说,这3种方法计算量均较小且相差不大,方便硬件实现。
在工程实现方面,M2M4方法具有不用载波相位的恢复、不需要接收机进行判决的优势,所以M2M4算法更适于应用在散射变速率通信中。
4 结束语
分析比较了3种复信道上的QPSK调制信号的盲信噪比估计算法。通过仿真和分析可以看出M2M4算法具有可估计的范围宽、估计精度高以及算法简单易实现等优点,在数据长度为200的时误差基本上都在1 dB之内。适合应用于变速率散射通信中。
[1]PAULUZZI D R,BEAULIEU N C.A comparison of SNR estimation techniques for the A WGN channel[J].Communications IEEE Transactions,2000,48(10):1681-1691.
[2]WIESEL A,GOLDBERG J,MESSER H.Non-data-aided signal-to-noise-ratio estimation.Communications.ICC 2002[C]∥IEEE International Conference,1:197-201.
[3]THOMAS C M.Maximum Likelihood estimation of Signal-to-Noise Ratio[J].IEEE trans.Common.,1968,COM-16:479-486.
[4]许 华,郑 辉.BPSK信号信噪比估计的一种新算法[J].通信学报,2005(2):50-53.
[5]BEAULIEU N C,TOMS A S,PAULUZZI D R.Comparison of four SNR estimators for QPSK modulations.IEEE Commun.Letters,2000,4(1):43-45.
