基于无抽取Haar算法的实时卡尔曼滤波方法

谭平，蔡自兴

(中南大学 信息科学与工程学院，湖南 长沙，410083)

卡尔曼滤波是最常用的最优状态估计方法，在满足线性和标准噪声(零均值、高斯分布)的条件下，通过递推形式得到最小二乘意义下的最优状态估计[1]。而基于小波多尺度分解的正交变换能够把单一尺度的状态估计转化到不同尺度上的状态估计，得到比原来单一尺度上好的处理效果[2]，特别针对 1/f类分形信号，小波变换可以使得不同尺度下的小波系数序列的自相关和互相关函数衰减很快[3-4]。为此，研究者们将小波多尺度分析和卡尔曼方法结合，提出了多尺度卡尔曼滤波方法。多尺度卡尔曼滤波能充分发挥小波变换与卡尔曼滤波的优点，取长补短，在信号去噪[5-6]、信号检测[7]、信息融合[8-9]、目标跟踪等方面效果明显。现有的多尺度卡尔曼滤波通常采用分段方式，先对状态序列进行小波多尺度分解，接着在各个尺度上进行卡尔曼滤波，然后通过小波重构得到状态估计值。但是，这种方式不满足在线实时处理，在进行多尺度分解时需要得到t时刻后的数据才能进行分解[10-11]，即在t时刻，不能同时得到不同尺度上的信息，而且存在较大的延时，特别是分解尺度越多，其延时越大。为了实时准确的得到各个尺度上的信息，本文作者提出基于无抽取Haar算法[12]的实时卡尔曼滤波，该方法能在t时刻获得各个尺度信息，降低了实时响应时间，另结合各小波阈值去噪方法，在信号处理方面表现出良好去噪性能。

1 多尺度卡尔曼滤波方法

1.1 多尺度动态系统建模

当采样时刻为t(t≥0)，在某一尺度j上建立动态系统：

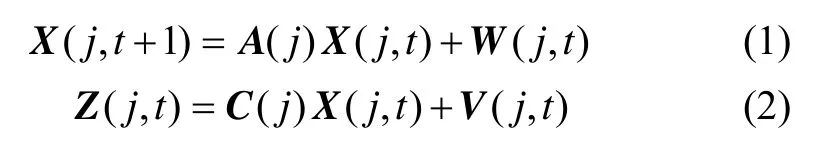
系统随机噪声序列和观测随机噪声序列满足：

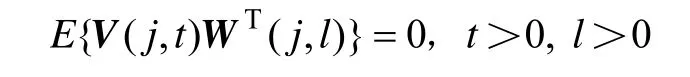
1.2 多尺度卡尔曼滤波方法

多尺度卡尔曼滤波方法(Multi-scale Kalman Filter，MKF)是在通过小波变换后，在各个尺度上对信号进行卡尔曼滤波[13]，图1所示为多尺度卡尔曼滤波的结构，其实现过程如图2所示。在计算时刻t的多尺度信号时，需要使用(t-2J-1)到(t+2J-1-1)(J为最大尺度)时刻的数据，因此其信号处理延时了2J-1-1个时间步长。当实时性要求较高时，将无法满足系统要求。

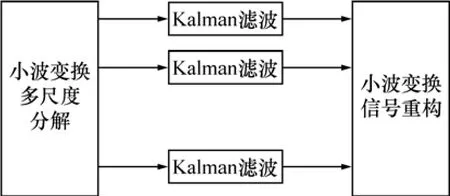
图1 多尺度Kalman滤波结构Fig.1 Structure of multi-scale Kalman filter

从图2可知这种方法存在以下2 个缺点：(1) 在t时刻计算得到的小波系数，不能为下次小波系数的计算所使用，需要重复计算，效率低；(2) 由于小波的对称性，为了计算t 时刻小波系数，需要延时2J-1-1个时间步长。图2 中延时为7 个时间步长，因此，实时性较差。

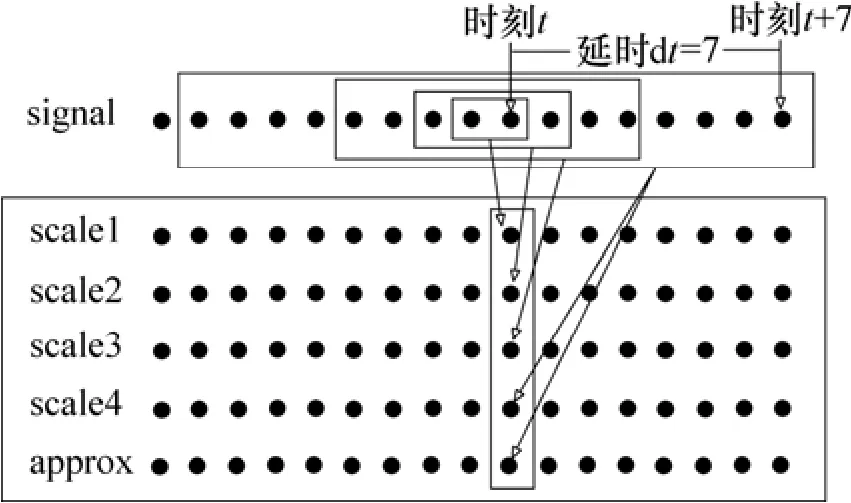
图2 t时刻小波变换中小波系数所使用数据示意图Fig.2 Input signal used to calculate wavelet coefficient at t time step

2 多尺度实时卡尔曼滤波算法

2.1 多孔算法

考虑时间序列信号{c0,t}，可定义为在t时刻函数f(x)与尺度函数φ(x)的内积，即

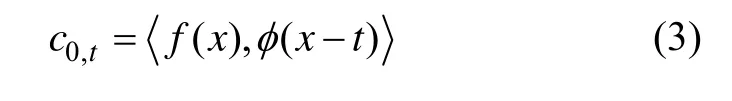
尺度函数满足方程：

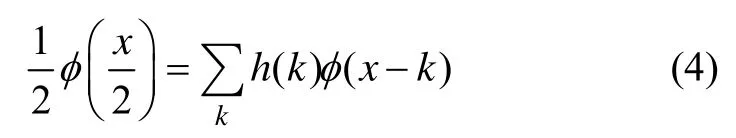
这里h是与尺度函数相关的离散低通滤波。由定义可知：信号通过低通滤波后与相邻尺度信号非常接近，而2层之间的距离通过因子2从一层增加到另一层。

在时刻t和尺度j下，逼近系数{cj,t}是函数f(x)与尺度函数内积：

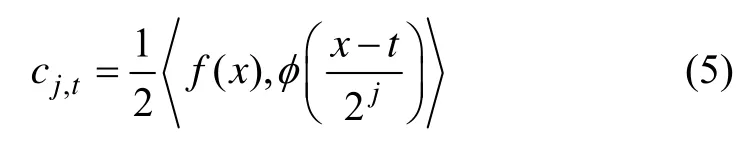
它也可以通过卷积计算得到：

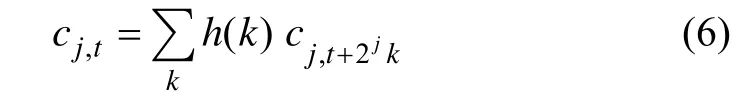
因此，连续2个层之间的差可以表示为：

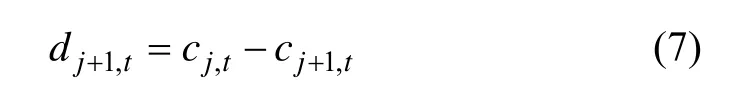
也可独立表达为：

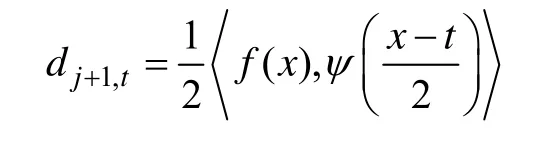
这里，小波函数定义为：

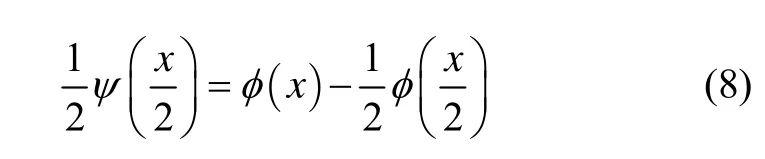
原始信号的重构可以表示为：

2.2 基于无抽取Haar算法的Kalman滤波

为了减少边界影响，同时提高变换的实时性，Renaud等[12]建议选用滤波器系数尽量窄的小波函数。并针对局部阶跃效应提出了无抽取Haar算法，该算法使用Haar小波基的低通滤波器h(k)={1/2,1/2}替换标准多孔算法，这里h是非对称的，考虑到第1层小波分解，可以使用原始信号与h进行卷积，则：

通过式(10)和(11)变换可知：在任意时刻 t，都不需要使用t时刻以后的数据来计算小波系数，因此，增强了实时性。显然该算法由于不需要平移信号，因此，信号＜x1，x2，…，xt＞在尺度j下的小波系数严格等价于信号＜x1，x2，…，xN＞的前t个小波系数，其中N＞t。该方法在实际中计算容易，只需要加减运算和右移运算即可完成，而且由于数据是进行有规律地更新，前面计算得到的小波系数可以为后面的计算使用，不需要重新计算，提高计算效率。

图 3所示为计算各个尺度逼近系数所用到的数据，对应的小波系数可以通过式(11)所得。

结合上面所提的快速计算方法，采用卡尔曼方法对各个尺度信息进行滤波，能有效提高收敛速度。为了提高精度，在小波分解后，在各个尺度上进行小波去噪，采用软阈值方法[14]，小波系数的去噪公式如下：

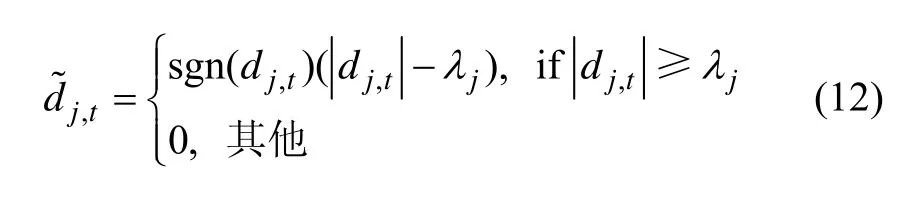
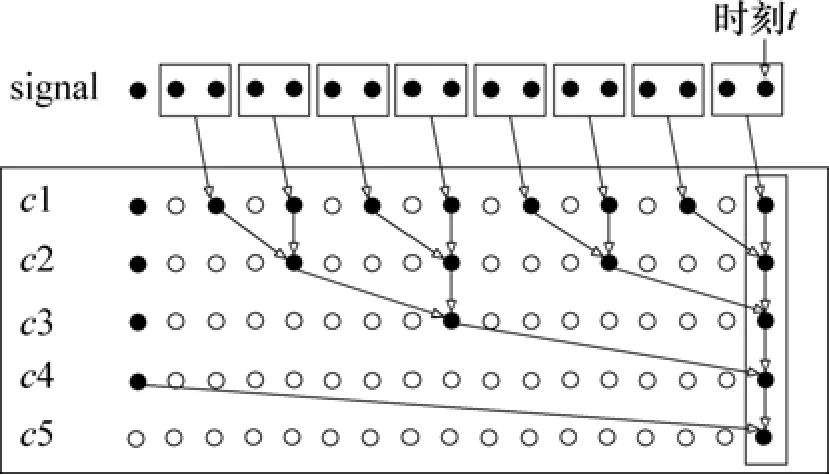
图3 t时刻小波变换中系数c所使用数据示意图Fig.3 Input signal are used to calculate approximation coefficient c at t time step in wavelet transform

图4 所示为基于无抽取Haar算法的实时多尺度卡尔曼滤波算法(Real time multiscale Kalman filter，RMKF)结构图。该算法的处理步骤如下(输入为t时刻采样数据xt；输出为t时刻滤波数据yt)：(1) 采用式(10)和(11)进行小波分解，令 c0,t=xt；(2) 利用式(13)在各个尺度上进行阈值去噪；(3) 在各个尺度上进行Kalman滤波；(4) 利用式(9)进行小波重构后得到滤波信号。

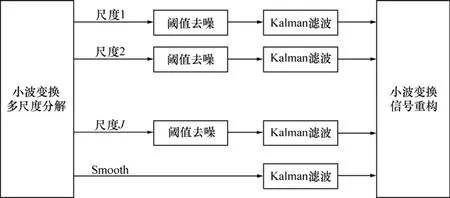
图4 多尺度实时卡尔曼滤波算法结构图Fig.4 Structure of multi-scale real time Kalman filter

显然，该算法能够在t时刻处理完数据，具有较强的实时性，其计算复杂度为 S=J×(4+Skf)(其中，J为最大尺度；Skf为卡尔曼滤波计算复杂度)。

3 实验结果及讨论

3.1 传感器去噪性能比较

为了验证该方法的效果，通过三轴低精度加速度和一个精度较高的 GPS/INS中惯性测量单元(Inertial Measurement Unit, IMU)进行验证，其中高精度数据作为参照对象。实验在中南大学自主改装的智能猎豹越野车上进行。

首先实时采集数据，然后分别采用小波阈值、普通卡尔曼滤波，MKF和MRKF 4种方法对低精度数据进行去噪处理，将结果与高精度的IMU加速度数据进行比较，这里采用均方误差(Mean square error，MSE)对性能进行评价：

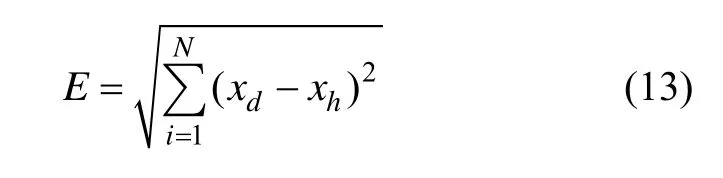
其中：xd为算法处理结果，xh为高精度传感器采集数据。图6所示为在设定状态转移误差为q=0.02时，4种算法对x轴数据的处理结果。为了验证算法的有效性，实验重复20次，结果取平均值，如表1所示。

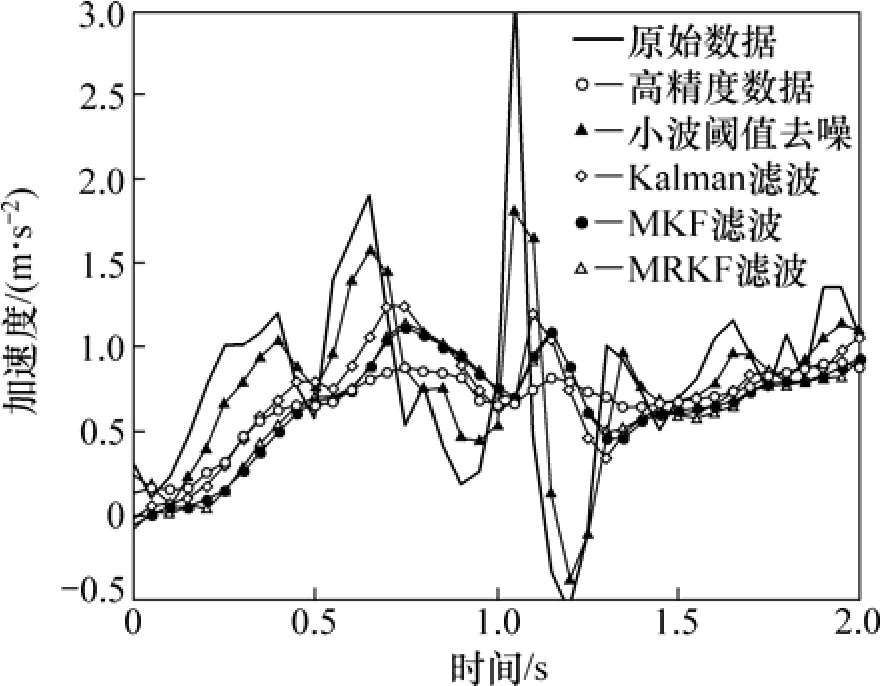
图6 4种算法对x方向加速度的处理结果Fig.6 Denoise result of four algorithms to x acceleration

表1 在q=0.02时，4种算法的均方误差Table 1 MSEs of four algorithms when q=0.02

从图 6可以看出：(1) 小波阈值去噪处理算法对匀速情况下能有较好的处理，但是在加速度变换特别是智能车颠簸时，处理后数据噪声依然很大，与实际数据依然相差很大。(2) 在状态转移误差估计准确时，Kalman滤波、MKF和MRKF对大噪声污染数据都有较好的处理能力，处理后的数据基本接近高精度数据。

为了验证实时性能，在采样速率为20 Hz，共有4个尺度的情况下，统计4种算法的平均延时，结果如表2所示。可见：Kalman延时最小，MRKF其次，小波去噪和MKF滤波时间较长，其原因是这2种算法本身需要等待2J-1-1个时间步长。

表2 4种算法平均延时Table 2 Average delay of four algorithms s

3.2 状态转移误差q对滤波结果的影响

对于一个动态系统，其系统状态转移误差通常比较难以估计，为了进一步比较Kalman滤波和RMKF的去噪能力，对系统方程中的状态转移误差q进行分析。设定状态转移误差q从0.001到0.700变化，对每个不同的q计算2种方法的均方误差，为了保证计算的统计特性，实验重复20次，取平均值得到结果如图7所示。由图7可知：(1) 存在最小估计误差，即误差估计有下限；(2) 当状态转移误差模型准确时，卡尔曼滤波是最优估计，q=0.01时，其均方误差最小；而q小于该值后，估计误差均方误差将显著增大，因此，实际中不能将状态转移误差设得太小。(3) 当状态误差模型不精确且q＞0.01时，多尺度卡尔曼滤波后的均方误差比普通Kalman滤波的小，其估计更精确。

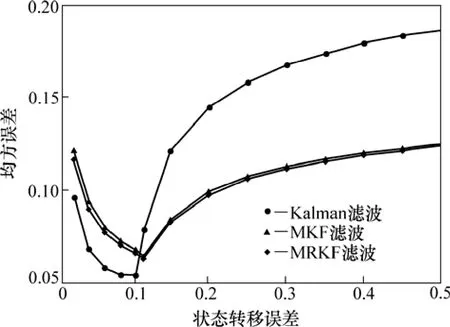
图7 3种算法的均方误差随系统状态误差估计变换Fig.7 MSEs of three algorithms with system state error estimated changes

因此，对于一个状态转移误差不能确定的系统，采用RMKF方法能有效提高系统的性能。

4 结论

(1) 提出了基于无抽取Haar算法的卡尔曼滤波实时处理方法，通过采用简单的加减、移位运算在t时刻完成多尺度变换，克服了基于分段式方法计算量大、实时性差的问题。该方法提高了算法实时性，并且有效减少重复运算，提高运算效率。

(2) 该方法结合小波阈值去噪，对强背景噪声数据具有较强去噪性能，并通过实验得到了验证。

[1] 徐宁寿. 随机信号估计与系统控制[M]. 北京:北京工业大学出版社, 2001: 135-141.XU Ning-shou. Random signal estimation and system control[M]. Beijing: Beijing Industrial University Press, 2001:135-141.

[2] 文成林. 多尺度估计理论及其应用[M]. 北京: 清华大学出版社, 2002: 115-121.WEN Cheng-lin. Multiscale estimation theory and its application[M]. Beijing: Tsinghua University Press, 2002:115-121.

[3] CHEN Bor-sen, HOU Wen-sheng. Deconvolution filter design for fractal signal transmission systems: A multi-scale Kalman filter bank approach[J]. IEEE Transactions on Signal Processing,1997, 45(5): 1359-1364.

[4] Hirchuren G A, Attellis C E. Estimation of fractal Brownian motion with multiresolution Kalman filter banks[J]. IEEE Transactions on Signal Processing, 1999, 47(5): 1431-1433.

[5] 柯熙政, 任亚飞. 多尺度多传感器融合算法在微机电陀螺数据处理中的应用[J]. 兵工学报, 2009, 30(7): 994-998.KE Xi-zheng, REN Ya-fei. The application of multi-scale sensor fusion algorithm to MEMS gyroscope data processing[J]. Acta Armamentarii, 2009, 30(7): 994-998.

[6] 覃方君, 许江宁, 等. 基于小波卡尔曼滤波的加速度计降噪方法[J]. 武汉理工大学学报: 交通科学与工程版, 2009, 33(1):49-52.QIN Fang-jun, XU Jiang-ning. A wavelet based kalman filter for accelerometers de-noising[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2009, 33(1):49-52.

[7] 尹世荣, 王蔚然. 多尺度卡尔曼滤波探测气体浓度[J]. 激光与红外, 2005, 35(9): 679-681.YIN Shi-rong, WANG Wei-ran. Multiscale kalman filtering gas concentration detecting[J]. Laser & Infrared, 2005, 35(9):679-681.

[8] ZHAO Tong-zhou, WANG Yan-li, WANG Hai-hui. Image Fusion Based on Multi-scale Kalman Filtering[C]//2010 Second International Workshop on Education Technology and Computer Science(ETCS). Wuhan, 2010, 3: 207-215.

[9] 崔培玲, 王桂增, 潘泉. 一类动态多尺度系统融合估计算法的分析[J]. 控制理论与应用, 2007, 24(1): 84-89.CUI Pei-ling, WANG Gui-zeng, PAN Quan. Analyzing of the fusion estimation algorithm of a class of dynamic multiscale system[J]. Control Theory & Applications, 2007, 24(1): 84-89.

[10] 时伟, 吴美平, 薛祖瑞. 基于小波卡尔曼混合滤波的激光陀螺信号处理[J]. 兵工自动化, 2005, 24(4): 57-58.SHI Wei, WU Mei-ping, XUE Zu-rui. Signal processing for laser gyro based on wavelet-kalman mixed filtering[J]. Ordnance Industry Automation, 2005, 24(4): 57-58.

[11] 丁宁, 周新志. 基于改进多孔算法的时间序列预测[J]. 系统仿真学报, 2007, 19(17): 4082-4085.DING Ning, ZHOU Xin-zhi. Time series forecasting based on improved Á trous algorithm [J]. Journal of System Simulation,2007, 19(17): 4082-4085.

[12] Renaud O, Starck J L, Murtagh F. Wavelet-based combined signal filtering and prediction[J]. IEEE Transactions on Systems,Man, and Cybernetics, 2005, 36(6): 1241-1251.

[13] 李强, 王其申. 1/f分形噪声的一种多尺度Kalman滤波方法[J].量子电子学报, 2007, 24(1): 7-12.LI Qiang, WANG Qi-shen. 1/f fractal noise attenuation using multiscale Kalman filter[J]. Chinese Journal of Quantum Electronics, 2007, 24(1): 7-12.

[14] Donoho D L. Denoising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627.