结构参数对费马型线柔性弹簧性能的影响分析
2011-07-30袁重雨祁影霞
袁重雨 陈 曦 祁影霞 刘 颖 李 静
1 引言
现代低温制冷机中压缩机采用直线电机驱动、间隙密封和柔性弹簧支撑等技术,改变了传统的活塞与气缸之间非金属弹性接触式密封方式,大大降低了活塞与气缸之间的磨损。柔性弹簧轴承作为压缩机动子共振系统中支撑排出器和压缩活塞的关键部件,在为活塞的往复振动提供较大的径向刚度、合适轴向刚度的同时,要保证运动活塞具有一定的行程。对保持排出器和压缩活塞在直线运动过程中活塞与气缸的密封间隙,防止活塞与气缸的直接接触,提高制冷机的寿命同样起到十分关键的作用[1]。
评价柔性弹簧性能的4个最主要指标[2-3]:疲劳强度、轴向刚度、径向刚度和自振频率。其中柔性弹簧的应力分布特性和径轴向刚度同其结构参数密切相关。上海理工大学陈曦[4]基于费马曲线,提出了一种新型费马型线柔性弹簧,其中可以调整的结构参数有起点半径A、涡旋系数B、曲线起始发生角φ、曲线略角θ、弹簧厚度以及涡旋槽的几何分布等。然而受压缩机气缸内径的限制,调节弹簧外径和内孔径的大小受限。本文主要通过改变曲线略角、厚度、涡旋臂数及封闭方式,分析这几个结构参数对柔性弹簧的刚度性能和最大应力值的影响,同时研究了一定略角范围内涡旋槽首尾封闭方式优化弹簧臂上应力分布集中的问题。
2 柔性弹簧的设计方法
费马方程:

费马曲线是根据费马方程(1)在平面上的齐次坐标所定义的代数曲线,其直角坐标方程式为:
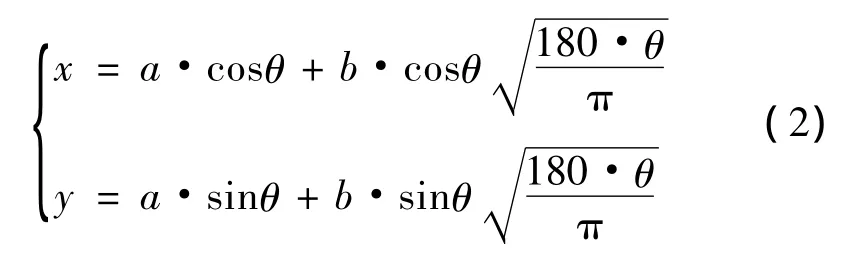
式中:a为曲线起点半径,b为曲率常数,θ为曲线涡旋角度。
在X-Y涡旋槽内、外侧上任意一点的坐标为:

式中:下脚标i表示涡旋槽内侧曲线上的参数,下脚标o表示涡旋槽外侧曲线上的参数,θ表示涡旋曲线略角,φ表示表示涡旋曲线起始发生角,n为略角常数,t∈[0,1]。其中通过改变曲线起始发生角φ和曲线略角θ,可以控制曲线的起始位置和终了位置,即得到不同圈数的涡旋槽,以满足不同内、外径尺寸柔性弹簧对涡旋槽型线的要求。形成弹簧涡旋槽后,必须将涡旋槽首尾端进行光滑的过渡封闭,防止由于非平滑过渡引起的应力集中,以提高弹簧的使用寿命。
按上述方法构造出平滑封闭的涡旋槽型线,按一定的规律在空间进行排列即可得到一组辐射状涡旋槽。根据设计要求,可采用不同数目的涡旋槽构成二臂、三臂、四臂或者多臂的柔性弹簧。
3 柔性弹簧的有限元分析
有限元法已在有关柔性弹簧性能研究的诸多文献中引用,并被证实是一种有效的分析方法[5-7]。基于本研究的斯特林制冷机气缸尺寸的要求,以外径为65 mm,内孔直径为 4 mm,厚度为 0.4 mm,略角为360°的三臂费马柔性弹簧为例,本文采用ANSYSY(10.0)软件对其进行分析,其中有限元分析的经典步骤:
建立有限元模型:导入弹簧片模型,通过PRO-E软件生成费马型线弹簧的三维实体模型,再将其转换为IGSE文件导入ANSYS(10.0)软件中;定义单元类型和材料属性,弹簧材料为优质硅锰弹簧钢(60Si2MnA),弹性模量为206 000 N/mm2,材料的密度为 7.908 g/cm3,泊松比为 0.3,许用应力为 900 MPa;划分网格,共19 561个单元,其网格划分如图1所示。

图1 0.4 mm柔性弹簧的网格划分Fig.1 Flexure spring meshing(0.4 mm)
加载和求解:在低温制冷机中柔性弹簧外边缘与气缸内壳固定,内孔与电机、活塞轴固定。于是在分析过程中设定的边界条件:柔性弹簧外边缘一周各结点的X、Y、Z方向移动、转动的6个自由度均被约束。在内边缘上分别施加轴向力、径向力和5 mm轴向位移,通过求解可以模拟出受外部载荷时对应方向上柔性弹簧的轴向位移和径向位移以及5 mm轴向位移时的最大应力值。
结果后处理:输出应力分布的等值图,应力均匀的分布在弹簧臂上(如图2、图3、图4)。柔性弹簧在5 mm轴向位移时的最大应力值为330.935 MPa。在轴向上施加1 N静态轴向力时,其最大应力值为95.605 MPa,对应的最大轴向位移为 1.501 mm。在经向上施加1 N静态径向力时,其最大应力值为13.33 MPa,对应的径向位移为0.008 9 mm。

图2 5 mm轴向位移时的应力分布图Fig.2 Stress distribution when axial displacement is 5 mm
4 结构参数对弹簧性能的影响及优化
结合有限元分析的结果,对设计的14种柔性弹簧的结构参数影响其最大应力值、径轴向刚度等性能指标进行了分析,结构参数和性能参数如表1。其中A和B分别表示两种不同封闭方式(如图8):A为槽尾端小半径封闭,B为槽尾端大半径封闭。a和b分别表示厚度为0.4 mm和0.6 mm。

图3 1 N轴向力时的应力分布图Fig.3 Stress distribution when axial force is 1 N

图4 1 N径向力时的应力分布图Fig.4 Stress distribution when radial force is 1 N

表1 柔性弹簧的结构参数及性能参数Table 1 Structure and performance parameters of flexure spring
4.1 结构参数影响费马型线弹簧性能的分析
随着略角的增大,涡旋型线长度也随之增加,即涡旋臂变长,弹簧在受不同方向的外部载荷时更易发生变形,同时较长的费马弹簧臂能分散弹簧臂上应力的集中。从第2—5、第7—10和第11—14这3组数据可看出三臂柔性弹簧随着略角的增大,5 mm轴向位移时的最大应力值、径轴向刚度均随着明显减小。以第2—5组数据为例,当略角为240°时,最大应力值为1 358 MPa(已远超过弹簧材料的许用应力值),轴向刚度为3.552 N/mm,径向刚度为1 459.8 N/mm;当略角为430°时,最大应力为272 MPa,轴向刚度为0.356 N/mm,径向刚度为 36.3 N/mm,相对于前者其最大应力值降低了80%,轴向刚度降低了10倍,径向刚度降低了40倍。图5—图7更清晰地反应了随着略角的增大,最大应力值、径轴向刚度明显下降。也就是说,当略角超过360°时柔性弹簧的最大应力值较小,有利于减少应力集中,但是径轴向刚度严重下降,不能满足压缩机用柔性弹簧的刚度要求。
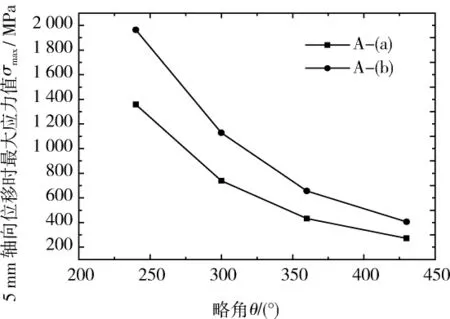
图5 不同厚度时最大应力值(轴向位移5 mm)Fig.5 Maximum stress value of different thickness when axial displacement is 5 mm
随着厚度增加,弹簧的抗拉强度增强。从2和7、3和8、4和9、5和10这4组数据可以看出,随着厚度的增加,5 mm轴向位移时的最大应力值、轴向刚度、径向刚度均随着明显增加,而且从这4组数据的轴向刚度对比可以看出,轴向刚度与厚度近似成3次方的比例关系,径向刚度与厚度成正比关系,这与文献[8]中的理论分析相一致。从图6和图7中也说明这一点:略角相同厚度不同的柔性弹簧轴向刚度曲线相隔较远,径向刚度曲线相隔较近。

图6 不同厚度时弹簧的轴向刚度Fig.6 Axial stiffness of different thickness of flexure spring
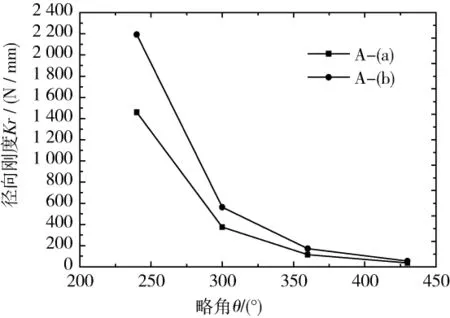
图7 不同厚度时弹簧的径向刚度Fig.7 Radial stiffness of different thickness of flexure spring
相同略角的涡旋型线,采用不同的弹簧臂数,涡旋臂宽也随之改变。从1和2、5和6这两组数据可看出,略角为240°四臂弹簧径向刚度为551 N/mm,5 mm轴向位移时最大应力为940 MPa,而三臂弹簧与之对应的值分别为1 459 N/mm和1 358 MPa;略角为430°三臂弹簧径向刚度为36.3 N/mm,5 mm轴向位移时最大应力为272 MPa,而二臂弹簧与之对应的值分别为211.4 N/mm和422 MPa,这说明减少弹簧臂数,能明显增加费马柔性弹簧径轴向刚度,但最大应力也随之增加,必然造成涡旋臂槽尾处应力过于集中,容易导致槽尾处出现断裂现象。
4.2 费马曲线结构参数的优化
型线首尾端的封闭方式在一定程度上能解决槽首尾处应力集中问题[9],采用较大半径的封闭圆弧平滑过渡能减小槽尾端封闭处的最大应力值。本文采用用B封闭方式对A封闭方式进行优化,如图8。

图8 两种不同的封闭方式Fig.8 Two kinds of closing method
从表1中的第2和11、3和12、4和13、5和14这4组数据可看出,增大封闭圆弧的半径,其5 mm轴向位移时最大应力值、径轴向刚度均减少。其中柔性弹簧的略角为300°和360°,分别采用A、B两种封闭方式时对应的最大应力值相差分别约为33.8%、23.6%,而当略角小于300o或大于430o时封闭方式对最大应力值的影响相对较小,如略角为240°的A、B两种封闭方式的柔性弹簧的最大应力值相差仅约为4.3%。这表明略角在300°—360°这一范围内封闭方式对费马柔性弹簧最大应力值的影响是很明显的(如图9)。又从图10和图11可看出,当略角大于300°时改变封闭方式对其径轴向刚度的影响很小,刚度变化不到15%。基于弹簧刚度的要求,当费马曲线柔性弹簧的型线略角处在300°—360°范围内时调节涡旋槽的首尾封闭方式能有效的降低最大应力值,又能保持柔性弹簧有较大的径向刚度和合适的轴向刚度,这对于进一步优化略角处在300°—360°这一范围内的费马柔性弹簧的性能有着重要作用。
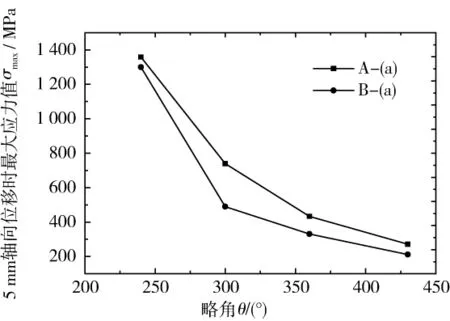
图9 不同封闭方式时最大应力值(轴向位移5 mm)Fig.9 Maximum stress value of different closing method when axial displacement is 5 mm
5 总结
通过分析费马柔性弹簧结构参数对上述几种柔性弹簧的最大应力分布和径轴向刚度变化特性的影响,归纳出以下几点结论:

图10 不同封闭方式时弹簧的轴向刚度Fig.10 Axial stiffness of different closing method for spring

图11 不同封闭方式时弹簧的径向刚度Fig.11 Radial stiffness of different closing method for spring
(1)随着略角的增大,费马柔性弹簧的最大应力、径轴向刚度均明显减小,当略角超过360°时,虽然此时最大应力值较小,但径轴向刚度严重下降,不能满足压缩机用柔性弹簧的刚度要求。
(2)费马柔性弹簧的轴向刚度与厚度的近似成三次方关系,径向刚度与厚度成正比例关系。同时增加厚度,弹簧的最大应力值也相应的随着增加。
(3)减少弹簧臂数,能明显增加费马柔性弹簧径轴向刚度,但最大应力也随之显著增加,必然造成涡旋臂槽首尾处应力过于集中,容易导致槽尾处出现断裂,降低弹簧的使用寿命。
(4)对于型线略角处在300°—360°范围内时,调节涡旋槽的首尾封闭方式能有效的降低最大应力值,同时保持费马柔性弹簧有较大的径向刚度和合适的轴向刚度,这对于进一步优化费马柔性弹簧的性能有着重要作用。
1 陈 楠.大冷量斯特林制冷机用动磁式直线压塑机关键部件及整机性能研究[D].上海:上海交通大学,2007.
2 陈 楠.涡旋柔性弹簧型线设计及有限元分析[J].中国机械工程,2006,17(12):1261-1265.
3 刘 颖,陈 曦,祁影霞,等,低温制冷机用柔性弹簧的研究进展及分析[J].低温与超导,2010(4):8-14.
4 陈 曦.柔性弹簧:中国,201010225430.5[P].2010.
5 Marquardt E,Radebaugh R,Kittel P.Design equations and scaling laws for linear compressors with flexure spring[C].Proc Int Cryo Conf,1992(7):783-804.
6 Gaunekar A S,Gddenhenrich T,Heiden C.Finite element analysis and testing of flexure bearing elements[J].Cryogenics,1996,36(5):359-364.
7 Wong T E,Pan R B,Johnson A L.Novel linear flexure bearing[J].Cryocoolers 7,1992:675-698.
8 刘 颖,低温制冷机用柔性弹簧的设计理论及工作特性研究[D].上海:上海理工大学,2011.
9 高威力,严鹏达,陈国邦.用于高频脉管制冷机的涡旋板弹簧的优化设计[J].低温工程,2009(1):5-8.
