三取二平台的时钟同步算法

2011-07-30潘雷

铁道通信信号 2011年12期

潘雷

*卡斯柯信号有限公司工程师，200071 上海

1 时钟同步介绍

高安全性、高可靠性系统经常会使用三取二平台作为系统处理器，尤其在铁路信号领域中，有些设备可能需要持续工作几年甚至几十年，并且系统安全完善度等级需达到SIL4，这些需求对硬件的搭建提出了许多苛刻的要求。在搭建三取二平台中，最重要的有2个功能:第1个是时钟同步;第2个是数据同步，也称为数据一致性比较。这里主要介绍时钟同步算法。

三取二平台中，3个通道独立工作，但需要进行准确的时钟同步，否则无法获取相同的输入值，也无法获得一致的运算时序，最终就无法进行三取二的运算而获取正确的结果，所以时钟同步对三取二平台而言是最为基本的功能需求。

在三取二平台的时钟网络中，由于3个通道分别工作，时钟是独立的，故系统无法得知真正准确的绝对时间。时钟同步的概念就是3个系通过某种算法协商出一个时间，同时需要证明这个协商出来的时间是一个最优的时间估值。

时钟同步理论中，一般将时钟同步分为2类:紧耦合时钟同步和松散耦合时钟同步 (又称宏时钟同步Macro-Synchronisation)。紧耦合时钟同步是指在同一个时钟控制下，所有CPU的执行时钟完全同步。从IEC61508中得知，三取二系统如果需要达到更高的安全性，需要降低三系之间的耦合度，以降低共模系数。在国外的一些三取二系统中，人为地让三通道错开一个小的间隙 (tick)进行运算，就是为了降低共模系数;同时由于现在的CPU内部都有锁相环，所以严格的物理时钟同步已经不现实了，现在广泛应用的三取二平台一般采用松散耦合的方式进行时钟同步。

这里主要讨论松散时钟同步方式。松散时钟同步下还有2类实现方式:硬件实现和软件实现。在本质上，这2种方式并没有什么区别，只是时间同步精度的差别。由于软件时钟同步需要一定的运算开销和数据传递开销，所以在时钟同步精度上无法和硬件时钟同步相比，通过对2种时钟同步方式进行验证后发现，相同的同步算法精度在2种情况下会相差一个数量级。

2 时钟同步基本概念

通过对相关参数进行数学量化，能够比较时钟同步算法的优劣。

2.1 时钟周期

这里关注的是T，为逻辑时钟，也就是需要同步的时钟;t为物理实际时钟，而C就是时钟同步方程。

2.2 时钟漂移

一个正确的物理时钟应该有一个正常的漂移范围，假设t2＞t1，则:

其中，ρ为最大物理时钟偏差，一般由时钟源的物理特性决定，从时钟提供者的数据手册可以查到，公式说明时钟漂移为有界的，正确的物理时钟与实际时间是线性关系。i代表通道号。

2.3 一致性

相同正确的物理时钟之间有一个正常的摆动范围:

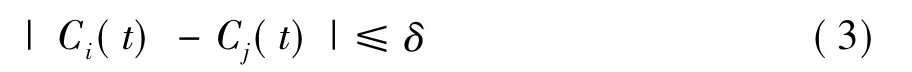
其中，i和j代表通道号;δ为同一频率的不同时钟之间的最大摆动。δ有界，它也是问题所在。如果时钟完全一致，那么也不存在同步问题。正是由于不同通道之间存在摆动，才有时钟同步问题，因此这个参数就是我们重点关注的。

2.4 精确性

存在常数γ＞0，它和a、b常数一起使得如下公式成立:

也就是时钟在有限时间内的误差可以被2个线性函数包含，即绝对误差有界。这也是同步时钟追求的，也就是说，不但要同步而且要精确。

在设计时钟同步器时，首先需要有这2个要求，然后才能提出合理的解决方案，选定不同参数去满足这2个需求。

满足一致性条件表明正确逻辑时钟之间的最大偏差是有界的;而准确性条件表明正确的逻辑时钟与实际时间是线性关系。

需要注意到γ是逻辑时钟漂移率的一个边界，同时它也是逻辑时钟的准确性。我们只对那些γ值最小的时钟同步算法感兴趣。而精确性公式 (4)能够证明γ≥ρ，所以只对满足这个条件的算法有兴趣。如果一个同步时钟算法是最优的，那么必须满足:任k≥1，t∈［endk，endk+1］，满足如下

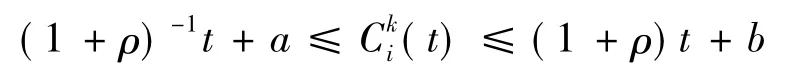
其中a，b与算法的初始化相关。

3 集中－非平均方式同步算法

在时钟同步算法中，有如下几种方式:集中方式、一致性方式和概率方式。这里不做详细介绍，比较常用的方式是集中方式，其下面又有集中－平均方式和集中－非平均方式。为了避免一个通道的失效影响到其他通道 (称为拜占庭式失效)，集中－平均方式需要至少4个及以上通道，才能做到避免拜占庭失效，它的理念基本上是取平均数，由于不适合三取二模型，这里也不做介绍，这里只介绍集中－非平均方法，适用于三取二的方式。集中－非平均方式同步方程涉及以下内容。

m为最大容忍错误通道数，n为通道数，需要满足如下条件n≥2m+1，在三取二中，n=3，m=1;每一个通道都周期性的寻求时钟同步 (分布式时钟同步)，每一个通道到达自己时钟周期时发布同步信息，同时在给定时间窗内接收到达的时钟同步消息，如果接收到m+1即2(如果是三取二的话，m=1)条信息，立刻启动同步，同时将接收到的信息向其他所有通道转发。见图1。

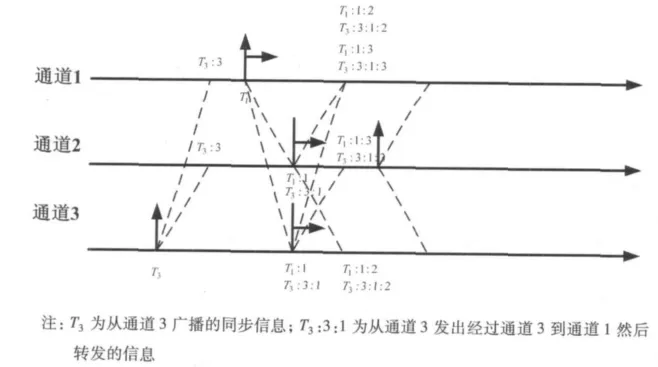
图1 通道时钟同步图

从图1中可以看出，假设通道3最快，通道1其次，通道2最慢。通道3最快而最先到达周期节点，那么它广播自己到达的消息给所有通道，然后等待。通道1第二快，它在自己的一个给定窗口内接收到来自通道3的同步信息，然后过一段时间它又接收到自己到达的消息，这个时候它相当于接收到了2个通道的同步消息了，可以重新启动同步计数器，并认定已经同步，同时将自己的同步消息广播出去，并传递所有接收到的消息给其他所有通道。

这个时候通道3接收到了通道1广播的消息和传递的消息，通过消息认定已经有2个通道到达同步了，也可以启动自己下一个同步周期。同样通道2接收到通道3广播过来的同步消息和通道1广播和传递的消息，通过消息确认也发现有2个通道已经到达了，所以不用等待自己的时钟周期是否真的结束，立刻重新启动新的时钟周期来保证同步。

本时钟同步方式并不是以最快的时钟为准，而是以中间的时钟为准，这里给出这个方程的一致性结果，如 (5)式，表1为 (5)式变量。

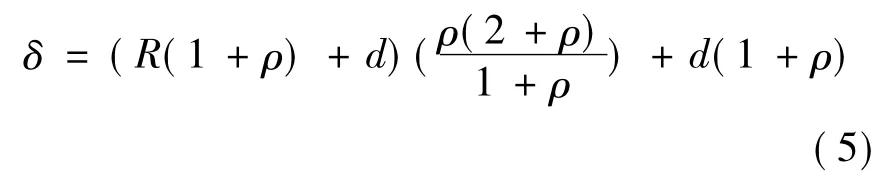
表1 变量参数表

d为信息传播延时 (通信延时加上消息验证延时)，上式近似为δ≈d+2ρR，在给定δ下，可以反推其他参数，这样就能设计出符合要求的定时器。

在试验中使用硬件和软件2种方式进行验证，R=1ms，即同步时钟周期为1ms，软件采用高速串口传输;硬件采用TTL电平互联，由于串口传输和验证d=50 μs，所以，软件方式的δ≈50 μs，而硬件传输延时可忽略，δ≈d+2ρR ≈2ρR ＜ 1 μs，试验结果与上述数据相当，可见使用此方法进行时钟同步可以取得比较好的同步效果。

4 初始化、升级操作

初始化操作:这个算法本身就带有明显的修正能力，在初始化过程中使用上述方式就能够完成初始化，只是初始化时对一致性没有要求，但是正常操作时，如果通道之间的一致性差别大于某个阈值的话，需要切断该错误通道。

升级操作:如果三取二降级为二取二后，经过维护，再次升级到三取二模式，当一个通道p想加入一个系统时，它发送 (加入)消息给系统中当前的所有通道，然后从这些通道接收到消息，被告知当前系统是出于哪个时钟同步阶段k，由于p可能是在同步周期的中期阶段开始它的算法，因此它要等到系统进行下一次时钟同步时方可加入。当通道p接收到k+1次时钟同步消息时，它将开始其逻辑时钟