水电站地下洞室群非线性地震反应数值仿真

张运良，郭 放

（大连理工大学建设工程学部水利工程学院，辽宁 大连 116024）

0 引言

近年来，大型水电站地下厂房洞室群的抗震问题在国内受到了重视，取得了不少成果[1-8]。由于所涉及的问题较复杂，该研究目前仍不成熟，尤其是对大型地下洞室群的三维动力非线性数值仿真还不多见，仍需结合具体工程积累研究经验。

本文以某抽水蓄能电站地下厂房为例，建立三维数值仿真模型，考虑初始地应力、分步开挖与锚杆及锚索支护，对主厂房洞室影响较大的不良地质体如局部蚀变岩的存在及岩体材料非线性等因素，考察地震作用过程中洞室围岩的位移、速度、加速度等时、频域反应特征，对主厂房洞室的围岩稳定性进行综合判别。本文的工作依托于FLAC3D软件平台，是文献[9]工作的深入，可为了解地下厂房洞室群的地震反应特点，进行动力稳定性复核积累经验，为设计提供参考。

1 基本理论与方法

本文采用带拉伸截断的摩尔-库伦直线形弹塑性模型来模拟岩体的屈服与破坏。

静力分析时，地表自由，模型四周法向约束，底部固定。在静力分析并达到平衡的基础上，进行输入地震作用下的动力分析，此时除地表仍为自由边界外，模型四周及底部采用基于平面波假设推导出的粘性边界。地震动输入在底边界施加法向和切向应力时程，与输入地震动速度时程相关；在模型四周侧边界施加自由场地震动。

有关动力分析理论及方法详见FLAC3D手册。

2 工程概况及计算参数

2.1 工程概况

某抽水蓄能电站地下洞室群主要由进水洞、主厂房、尾水洞、调压井等组成，其中主厂房洞室开挖尺寸为 156．66 m×21．5 m×46．17 m （长×宽×高），垂直埋深约105～150 m。电站引水系统采用l洞1机的布置方式，尾水系统采用1洞2机的布置方式。电站装机容量为4×150 MW。设计地震基本加速度为 0．05 g。

2.2 计算参数

由于洞室规模较大，工程地质条件复杂，虽然设计地震加速度水平较低，但为了保证其在地震作用下的围岩稳定性，且为了解大型地下洞室群的地震反应特点，进行动力分析。

（1）洞室大范围岩体主要为III类灰岩。在1号、2号机组段发育有花岗闪长斑岩蚀变带，在厂房上游边墙及局部顶拱有较大范围的出露，蚀变程度严重，力学指标较低，不利于厂房稳定，其位置见图1a。在洞室开挖过程中，主厂房洞室顶拱及边墙施加了钢锚杆进行加固，其几何参数为直径 （φ）25 mm，长度 （L）为5 m或7 m。另外，在边墙部位还施加了预应力为1 000 kN的对穿钢锚索，其参数 φ 为 15．24 mm， L为 15～21 m。

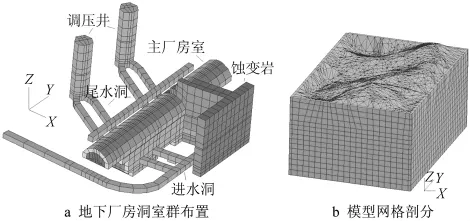
图1 地下洞室群布置示意及三维整体有限元差分网格

（2）地下洞室群的静、动力分析三维整体计算模型网格剖分见图1b，模拟了尺寸较大的1号～4号主厂房洞室，4条引水洞、4条尾水洞及2个调压井室。地表根据实际地形资料建模。岩体采用实体单元划分，锚杆和锚索采用FLAC3D中的锚结构单元进行模拟。模型沿主厂房洞室轴向总长717 m、高320 m、横向宽490 m，共剖分单元59 370个，节点18 025个。整体坐标Y方向与主厂房洞室轴向一致，Z轴竖向向上为正向，X向为厂房机组段横向。为了输入地震动的需要，将模型四周在某一高程取平。为满足波动传播的精度要求，网格竖向尺寸最大控制为20m。

（3）计算仅模拟了对主厂房洞室稳定性影响较大的蚀变岩脉，不考虑离主厂房洞室较远的裂隙和小断层。 材料静、 动力参数统一取值[10]（见表1）。计算中设水泥浆的内摩擦角、与岩孔孔壁及钢筋的粘结强度、锚杆和锚索的抗拉、抗压强度足够大，以模拟支护具有足够的加固能力。

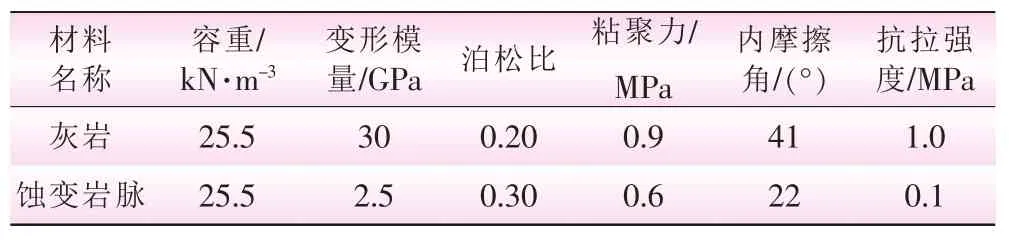
表1 材料参数

（4）在静力计算开始时，首先，施加初始地应力场。根据实测地应力资料，利用神经网络技术，反演得到水平构造应力场σx、σy与竖向自重应力场σz=γh的关系[11]。其次，模拟主厂房洞室分步开挖过程，断面开挖自洞顶至洞底共分6步进行，每一步均需应力重分布计算。开挖结束待平衡后，进行动力分析。考虑地震波竖直向上传播且三向同时输入。图2给出了调幅后的三向输入速度时程，该时程系由美国原子能RG1．60谱生成的人工地震加速度波经积分后得到。

图2 地震输入速度时程曲线

（5）计算采用动态多步长方法，时间步长量级为10-6s，地震持续时间为28．0 s。岩体阻尼比取0．05， 局部阻尼系数取 0．157[10]。模型建立完毕后， 采用FLAC3D内部Fish语言编程进行计算和结果提取。

3 结果分析

3.1 动力反应分析

选取高度最大、与蚀变岩相交部位的主厂房洞室断面进行结果分析。取该断面上的关键点见图3，其横向地震反应时程曲线见图4。

从图4可以看出，开挖结束后 （即地震作用前t=0 s时刻），断面内沿洞室高度各点均具有非零的横向 （即X向）初始静位移，在其后的地震作用过程中各点横向动位移的波形变化非常相似，且几乎同步。这一规律也反映在横向速度和加速度反应时程曲线上。这可能是因为地下岩石洞室跨度及高度不到百米，介质波速达数千米级，因此，各点的反应几乎无相位差别。

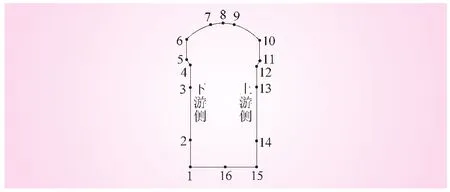
图3 主厂房洞室断面及其关键点

由动力反应时程最大值可知：①各关键点的横向动位移、速度和加速度反应沿高程相差不大。②各点的主应力均表现为压应力，在洞脚处最大，在洞顶和洞底次之，洞腰最小。该主厂房洞室围岩在地震作用过程中没有产生受拉破坏。③与输入速度幅值相比，各点速度反应放大系数约为1．3～1．6倍。④与输入加速度幅值相比，各点加速度反应放大系数约为 1．3～1．9 倍。

对比横向输入速度 （图2）与反应速度时程曲线 （图4b）可看出，由于存在介质阻尼 （包括几何辐射阻尼），最大反应速度时刻 （t=9．99 s）稍滞后于最大输入速度时刻 （t=9．69 s）。图5给出了横向速度反应的傅里叶频谱，经与输入速度频谱比较后可知，二者均在0．27 Hz处谱值最大。这表明，地下主厂房洞室岩壁横向速度反应与输入波形基本相符，只是幅值稍有放大，并且反应为低频震动。

3.2 稳定性分析

在横向速度反应达最大时刻 （t=9．99 s）， 主厂房洞室断面的塑性区见图6，并与开挖结束后（即地震作用前t=0时刻）及地震作用结束后 （t=28．0 s时刻）进行了对比。

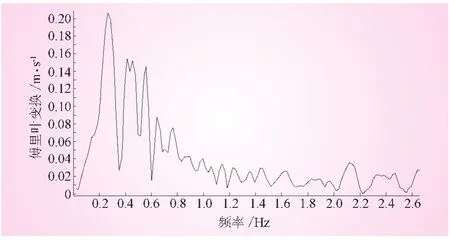
图5 主厂房洞室关键点的横向反应速度傅里叶频谱

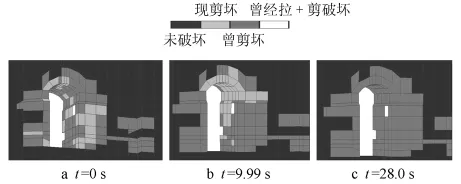
图6 主厂房洞室围岩不同时刻的塑性区比较

由图6可以看出，开挖结束后及地震作用过程中，主厂房洞室围岩基本上未发生拉破坏。地震作用使得剪切塑性区从洞顶局部较小范围进一步扩大至全部洞顶，且在上游蚀变岩存在的洞肩及边墙中上部，沿洞室跨度和轴线方向，塑性区延伸范围扩大 （深约15 m）并在洞顶形成贯通，从而不利于洞室围岩的稳定，设计中要注意洞顶坍塌的危险。然而，地震作用结束后，上述呈现塑性的洞周岩体恢复为弹性。

隧洞稳定性的判别可依据三个条件[10]：①隧洞周边是否有围绕隧洞的塑性贯通区；②设置在隧洞周围的关键点的位移是否出现突变；③计算中节点不平衡力和位移是否收敛。本文洞周关键点的位移没有出现突变，计算中力和位移都达到收敛，且除洞顶和上游洞肩部位需要加强支护 （设置更长的锚杆穿过塑性区）外，可以认为地震作用下该洞室的动力稳定性基本可以保证。

4 结语

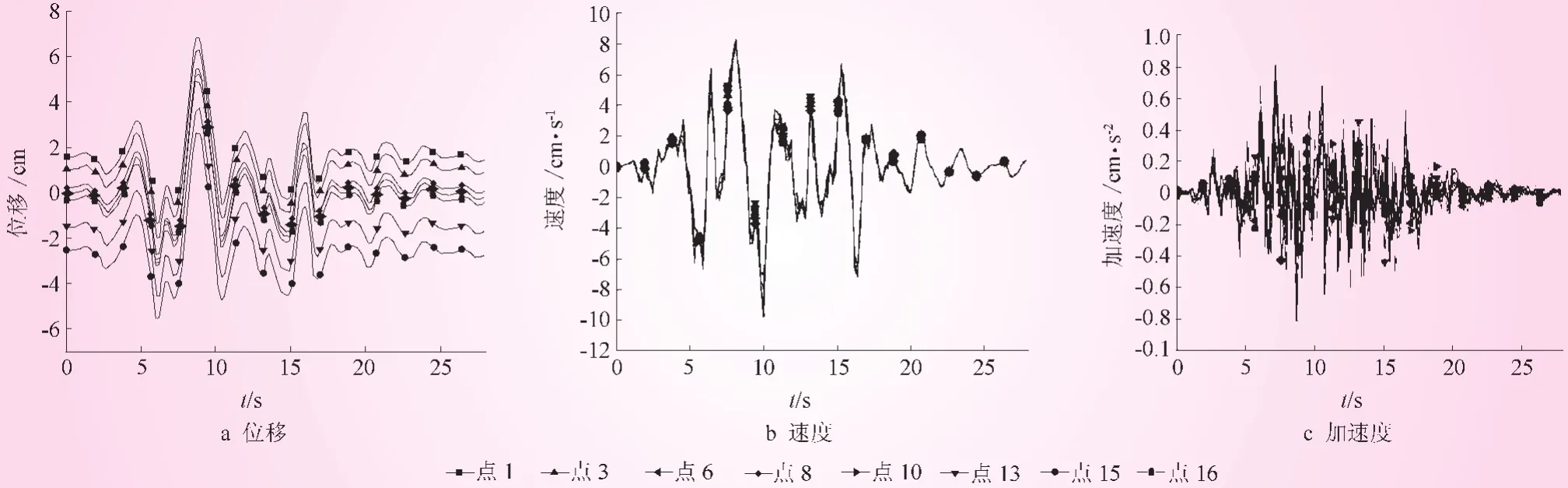
图4 主厂房洞室关键点的横向地震反应时程曲线

地下洞室群的地震反应数值仿真是一个相当复杂的课题。在进行动力分析时须适当地考虑工程地质条件、初始条件、施工支护过程和岩体材料的非线性。在对FLAC3D二次开发的基础上，本文通过某抽水蓄能电站地下洞室群非线性地震反应的仿真分析，认为对于岩石地下洞室工程，围岩的地震反应属低频震动，且同一断面内沿高程主厂房洞室岩壁各点的位移地震反应波形基本相似，相位差别非常小。速度和加速度反应具有类似的规律，且其波形与输入波形基本相符，只是幅值稍有放大。

本文采用的工程设计地震加速度代表值 （0.05 g）较低，尽管震后洞周岩体恢复为弹性，地震作用并未严重扩大和加剧洞周围岩的塑性区分布范围，但对于我国西部高烈度频发强震区，强地震作用对大型地下厂房洞室群的围岩稳定性影响不容忽视。

［1］ 陶连金，张倬元，傅小敏，等.在地震载荷作用下的节理岩体地下洞室围岩稳定性分析［J］.中国地质灾害与防治学报，1998，9（1）:33-41.

［2］ 金峰，王光纶，贾伟伟.离散元-边界元动力耦合模型在地下结构动力分析中的应用［J］.水利学报， 2001（2）:26-30.

［3］ 李海波，马行东，邵蔚，等.地震波参数对地下岩体洞室位移特性的影响分析［J］.岩石力学与工程学报， 2005， 24（A01）:4627-4634.

［4］ 隋斌，朱维申，李晓静.地震荷载作用下大型地下洞室群的动态响应模拟［J］.岩土工程学报， 2008， 30（12）:1877-1882.

［5］ 李小军，卢滔.水电站地下厂房洞室群地震反应显式有限元分析［J］.水力发电学报， 2009， 28（5）:41-46.

［6］ 王如宾，徐卫亚，石崇，等.高地震烈度区岩体地下洞室动力响应分析［J］.岩石力学与工程学报， 2009， 28（30）:568-575.

［7］ 左双英，肖明.映秀湾水电站大型地下洞室群三维非线性损伤地震响应数值分析［J］.水力发电学报， 2009， 30（3）:721-728.

［8］ 崔臻，盛谦，刘加进，等.基于小波包的地下洞室群地震响应及其频谱特性研究［J］.岩土力学， 2010， 12（31）:3901-3906.

［9］ 张运良，马艳晶，韩涛.大型水电站地下洞室群三维地震反应时域分析［J］.水力发电， 2010， 36（5）:27-30.

［10］ 郑颖人，肖强，叶海林，等.地震隧洞稳定性分析探讨［J］.岩石力学与工程学报， 2010， 29（6）:1081-1088.

［11］ 张国强.水电站地下厂房洞室群施工数值模拟［D］.大连：大连理工大学，2007.