按挠度优化混凝土板配筋的应用
2011-07-25秦瑞奇
秦瑞奇
(赵县建筑公司,河北赵县051530)
节能降耗是环境保护的重大课题,降低建筑物的单平米耗钢量渐渐引起重视。在结构设计中,混凝土板是按两个支座或连续支座来计算的,并选择最不利的受力状态(板中)设计,这样势必造成无辜的材料浪费。从混凝土板施工“起拱”开始,客观分析其挠度本来不同的现象,按四边支座对其进行分析,方法简单易懂,但阐明了几个重要概念,值得深入研究,在设计、施工中推广应用。
1 砼板挠度与钢筋受力的关系
根据力与物体变形的关系可知,物体在外力的作用下会产生变形,绝对不变形的物体是不存在的。反之,同一物体产生不同的变形,那么该物体肯定在不同的力的作用下。
混凝土板在荷载作用下,中部向下弯曲,弯曲变形大小常被称为“挠度”。挠度大的部位受力钢筋应变大,挠度小的部位受力钢筋应变小。即使受力点不在板中心,但挠度的最大值偏向板中(如图1)。

图1 挠度的最大值偏向板中
在施工过程中,进行混凝土顶板模板支设时,要预设拱度,即“起拱”,起拱值的大小在施工规范上有明确要求:板跨度的1/1 000~3/1 000[1]。当混凝土顶板模板支撑体系拆除后,板因自重下垂,产生的挠度正好与预先起拱的高度相抵消,最终板底面基本水平,以满足施工规范的要求。在此,混凝土板起拱的高度在各部位显然是不同的,故得知:混凝土板从成型起,其各部位的挠度是不同的;在荷载作用状态下,各部位的挠度更是不同的。
如图2,一块周边支撑于墙体或混凝土梁的混凝土板,将其划分若干区域(分区方法:1区、2区为无扣筋区;3区、4区、5区为有扣筋区),无论在集中荷载、均布荷载、动荷载的作用下,各区域的挠度不尽相同,配筋也应该可以各不相同,这就是根据挠度分区配筋的基本思路。
1.1 在受底筋约束区
2区的挠度小于1区的挠度,2区Y向配置的底板筋数量也应小于1区的Y向配置的底板筋数量;同理,5区Y向配置的底板筋数量也应小于2区Y向配置的底板筋数量。5区与支座的交接处,挠度为零,则此处Y向配置的底板筋满足构造要求即可。形成一种“从中心到边缘底板筋配筋量逐渐减小,一直降为满足构造配筋要求”的形式。
若为双向板,因4区的挠度小于1区的挠度,故X向配置的底板筋数量也应小于1区X向配置的底板筋数量。
在4、5区板边部位,施工过程中可以发现,与梁、墙相邻且平行的第一根底板筋根本起不到一点作用,无论对抗弯还是抗剪能力。
1.2 支座扣筋约束区
4区扣筋末端的挠度大于3区扣筋末端的挠度,4区Y向配置的扣筋数量也应大于3区Y向配置的扣筋数量;5区扣筋末端的挠度大于3区扣筋末端的挠度,5区X向配置的扣筋数量也应大于3区X向配置的扣筋数量。形成一种“从边(墙或梁)中心到角部扣筋的布置配筋量逐渐减小,一直降为满足构造配筋要求”的形式。

图2 混凝土板分区示意图
在3区板角部位,施工过程中可以发现,与梁、墙相邻且平行的第一根扣筋根本起不到一点作用,无论对抗弯还是抗剪能力。并且,4区、5区中部挠度较大,越接近3区挠度越小,在与挠度变化方向相垂直的支座处:墙、梁边降为零。
通过前述分析,得出结论1:混凝土板中梁、墙边第一根钢筋(底筋或扣筋)应按构造配置,即第一根钢筋距梁、墙边应为150~200 mm,钢筋规格与其它位置钢筋相同。
2 按四边支座对混凝土板进行受力分析
假设相同的荷载N作用于图2中1区、2区时,四边支座均产生支座反力,轴侧简图如图3和图4:支座A、支座B分别作用于③轴、④轴,支座C、支座D分别作用于B轴、C轴。
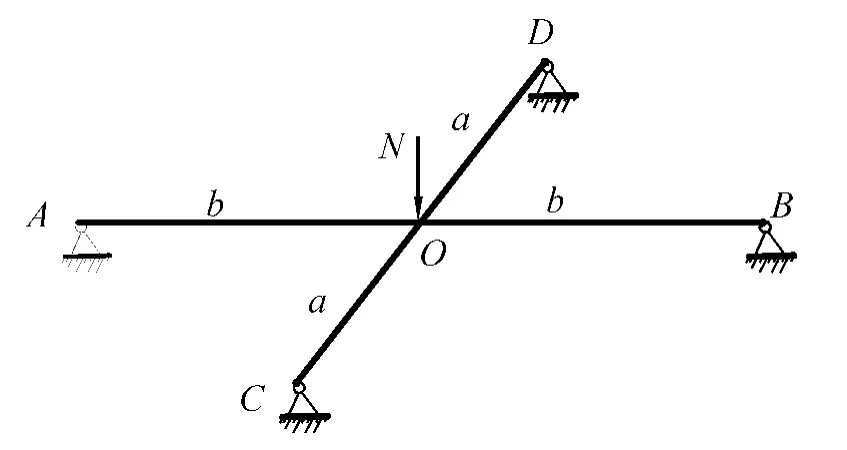
图3 力作用于混凝土板中心

图4 力作用于混凝土板2区
在图3中,荷载N作用于混凝土板中心,将轴侧图变为俯视图(如图5)。视荷载N由△AOC和△BOD共同支撑,FAC=FBD=N/2。在△AOC中,OE⊥AC,EC=a2/EA=b2/FA=Na2/2(a2+b2),FC=Nb2/2(a2+b2)。
将a=2 m,b=3 m,代入得FA=0.153 8N;FC=0.346 2N。△AOC和△BOD点对称,可知FB=FA=0.153 8N;FD=FC=0.346 2N。可见,a与b值相差越大,支座反力也就相差越大。
在图4中,假设a=2 m,b=3 m,x=1 m,将轴侧图变为俯视图(如图6)。视荷载N由△AOC和△BOD共同支撑。E、F是中点,OG⊥EF,EF是两个三角体的虚拟作用线。通过几何运算或CAD测量,可得:EG=1.388 m,GF=2.218 m,EF=3.606 m。则得:FAC=N·(2.218/3.606)=0.615 1N;FBD=N·(1.388/3.606)=0.384 9N;FA=FC=(1/2)·FAC=0.307 6N;FB=FBD22/(22+42)=0.384 9N·(1/5)=0.077 0N;FD=FBD-FB=0.307 9N。(FA、FC、FD基本相等)。
结论2:在混凝土板中,当荷载作用点距支撑点距离相等时,支座反力基本相等。
矩形混凝土板中,距三边距离相等的点暂且命名为“等距点”。在等距点底板短向钢筋受力使混凝土板产生的挠度和与底板长向相平行的扣筋受力使混凝土板产生的挠度相等。混凝土板底面破坏断裂线的交点与等距点关系密切[2]。

图5 力作用于混凝土板中心(俯视图)

图6 力作用于混凝土板2区俯视图(单位:m)
现行设计中,砖混结构的非承重墙、框架结构的连系梁,均按不承重考虑,但实际上它们一样承受荷载。砖混结构的非承重墙可看成“拱”,拱的挠度较小,刚度较大。框架结构的连系梁的刚度远远大于混凝土板的刚度,连系梁两侧板的荷载,首先传递给连系梁,再由连系梁传递给主梁(或柱)。它们两者均未因规定而失去在建筑物中的作用。
因此,倡导适当提高非承重墙、连系梁上部混凝土板扣筋的配筋率,这样更切合实际。
数据分析,按a=2 m,b=3 m,x=1 m,结果如表1。
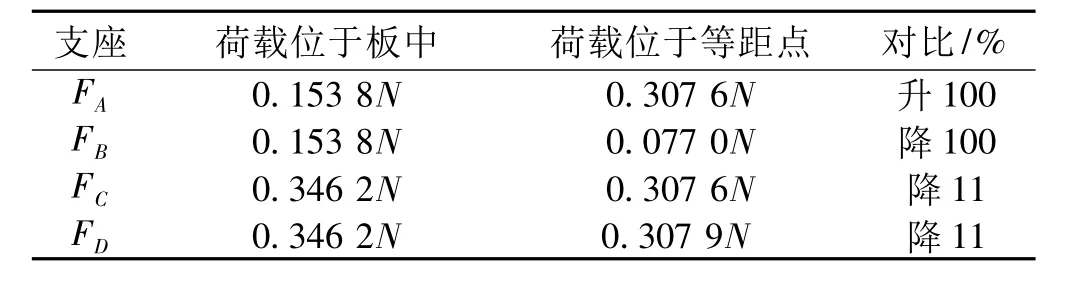
表1 荷载作用于板中、等距点时四边支座反力对比表
图6俯视图实际是图5俯视图中CD杆件向A支座移动1 m(共可移动3 m),A支座受力增加1倍,B支座受力减少1倍;短向C、D支座受力降低约11%。如果图6俯视图中CD杆件向A支座继续移动,短向C、D支座受力继续降低,当CD杆件与A支座重合时,C、D支座受力为零,A支座(横墙或连系梁部位)承受全部荷载。可见,混凝土板中部配筋应最大,板边缘配筋应最小,在降低的过程中,配筋变化率开始很小,然后越来越大,与抛物线的形式极其相似。
根据以上可推出:在混凝土板中,板边缘配筋率最小,一般满足构造要求即可,板中间部位配筋率最大。与挠度曲线对应,基本可按二次函数y=ax2+bx+c的形式进行配筋。当a<0时,方程最大值即是板中最大配筋率。
3 混凝土板配筋优化初步探索
例如:图2一混凝土板(连续板),净开间3.00 m,净进深5.00 m(③轴-④轴),底板主筋配置Φ10@100(可视为1区配筋率:785 mm2/m),扣筋为Φ10@150,板厚100 mm。
根据结论1:混凝土板中梁、墙边第一根钢筋(底筋或扣筋)应按构造配置Φ6@200[3],得梁、墙边配筋率:141.3 mm2/m(可视为③轴-④轴内边缘配筋率:141.3 mm2/m;说明:边缘挠度为零,本应配筋率为零,此处按构造配筋取值,可视为安全系数取值)。
将以上两状态看成方程y=ax2+bx+c的两个条件(其中x为距③轴的距离,y为底板主筋配筋率):x=0、50 dm时;y=141.3;x=25 dm时;y=785(即:-b/2a=25时;(4ac-b2)/4a=785)。将以上两条件,代入方程y=ax2+bx+c得:a=-1.03;b=51.5;c=141.3。则抛物线方程式为:y=-1.03x2+51.5x+141.3。混凝土板底板筋应遵循此方程配置。计算x=5、10、15、25 dm……时,y=373、553、685、755、785;……。
图7建立坐标系,标出x=5、10、15、25 dm等各点的配筋率。绘制抛物线。配置区段钢筋。但降低配筋率部位需进行验算。
(1)抗剪方面。以x=5~10 dm区段为例,底筋改为Φ10@140后,支座处扣筋、底筋总截面为5.42 cm2,乘以钢筋的抗剪强度12.5 kN/cm2,得钢筋抗剪力为67.7 kN;活荷载按3.5 kN/m2计,加上恒载5.25 kN,总荷载值为10.5 kN,即使按“等距点”三分荷载考虑,支座处的总剪力只3.5 kN;不计混凝土抗剪力,钢筋抗剪力亦可满足抗剪要求。若不能满足抗剪要求,需加设30°(或45°)抗剪斜筋、垂直拉钩[4](如图8),以求最大限度降低经济技术指标。

图7 按二次函数重新配置底板主筋
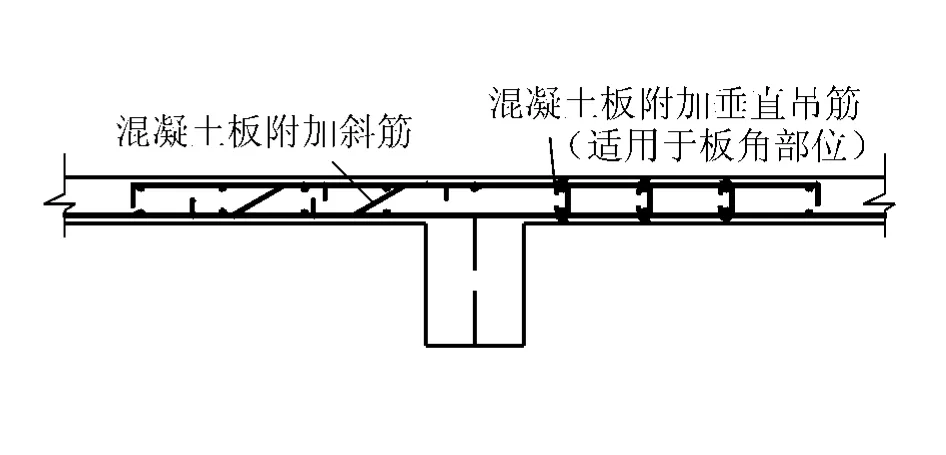
图8 混凝土板附加斜筋、吊筋抗剪示意图
(2)抗弯方面。在“等距点”配筋降为Φ10@110,仅降低了10%;根据结论2可知,此处的荷载三等分后,区段荷载降低了30%,荷载降低的百分率是配筋降低百分率的3倍,肯定满足抗弯要求。
重新绘制底板配筋图(如图9)。推荐表示方法如下:Φ10@100/110/140/200(500),其中(500)表示划分区段的宽度,100/110/140/200分别表示区段中配筋的间距。
扣筋部位剪力较大,以考虑抗剪、抗负弯矩为主,不便于按此方案优化配筋。

图9 混凝土板底筋优化布置图(单位:mm)
4 结论及建议
就以上案例,如图9,按照常规设计施工,需要使用Φ10钢筋51根。按照优化布置施工,需要使用Φ10钢筋41根。底板主筋将节约19.6%。
方案一样适用于地下室挡土墙、池体外壁,不适用于高层建筑边跨房间[5]。
尚需解决的问题及建议:
(1)“等距点”、“混凝土板按四边支座计算”的问题需更深入探讨。
(2)方案的可操作性、方便使用性还需探索,如研制一种伸缩尺,可很快标出钢筋的间距,解决钢筋变距的问题。
(3)优化计算中运用“微积分”运算,效果更佳,但要适当提高安全系数。
[1]徐占发.建筑施工[M].2版.北京:机械工业出版社,2011.
[2]薛建阳,王威.混凝土结构设计[M].北京:中国电力出版社,2010.
[3]王文栋.混凝土结构构造手册[M].3版.北京:中国建筑工业出版社,2003.
[4]蓝宗建.混凝土结构[M].北京:中国电力出版社,2011.
[5]杨嗣信.高层建筑施工手册[M].北京:中国建筑工业出版社,1992.
