基于桥梁结构的动态称重系统算法研究

耿少波， 石雪飞， 阮 欣

(同济大学桥梁工程系，上海200092)

0 引言

随着我国公路桥梁及城市桥梁的大量建设，在役桥梁承载能力评估吸引了越来越多的桥梁研究者的目光，而汽车荷载作为在役桥梁最重要的活载之一，明确其分布特点具有重要意义。动态称重系统为汽车行驶过程中无需停车即可测得其所有参数的装置和设备，目前主要有两种采集方式。第一种为路面式动态称重系统Weigh-in-Motion(WIM)，即将传感器埋入快进入桥梁结构的行车道路面下方，这是早期最先发展起来的测量系统，主要优点为适合任何桥梁结构并可长时间采集数据，缺点为价格昂贵，安装时需阻碍交通，传感器不能循环使用。第二种为基于桥梁结构应变的动态称重系统Bridge Weigh-in-motion(BWIM)，适合于中小跨径桥梁结构，携带及安装方便，价格较低，可循环使用，缺点为适用范围较小。总体来说，这两种方法均克服了地磅称重需停车的不便，并可以测得车速、轴距、车头间距等静态称重无法测得的物理量。

我国在役桥梁结构分布中，绝大多数为中小跨径桥梁，而目前的在役中小跨桥梁承载能力评估中缺少了其服役汽车荷载的真实分布调查，BWIM的系统开发与使用可弥补这方面的不足。Snyder［1］在1972年最早提出了可利用桥梁作为汽车荷载测量平台。随后，Moses［2］在1979年给出了汽车轴重计算的一般原理，但未对标准车下桥梁结构影响线的标定方法进行说明与求解，而影响线的求解精度是贯穿轴重求解的重要指标。此后Peter［3］将此思路移植到了涵洞上进行测试，研制出了CULWAY系统，ZAG在2001年开发了SIWIM系统，实现了商业运营，2008年推出了FAD版本，使设备的操作更加简化。我国在20世纪90年代初便开展了WIM系统研究，但在BWIM研究方面比较缓慢，见于文献的资料很少，现针对BWIM的系统开发算法进行研究，为系统开发提供理论支持。

1 算法原理

当移动荷载在简支梁桥上移动时，弹性范围内，随着荷载的增加，其结构中的应力与荷载大小成正比，第i片主梁产生的截面下缘应力为

式中，i表示任意第i片主梁，若主梁总数为m，则i取值范围为1～m;σi表示第i片主梁中产生的应力;Mi表示第i片主梁所承受的由外荷载引起的弯矩效应;Wi表示第i片主梁的抗弯截面系数，与横截面的形状和尺寸有关。

一般情况下，一座桥梁中每片主梁采用的混凝土标号相同，意味着每片主梁的弹性模型可以取为一相同值E，根据混凝土本构关系为线弹性时，公式(1)可以写为

式中，εi表示第i片梁中的应变。

假设主梁截面相同，则各主梁弯矩之和为

因此，主梁测得的应变之和将正比例于梁桥整体所受的弯矩。应变之和可以由WIM系统的应变传感器测得，EW分别为材料和截面属性，对于在役桥梁而言，可以实测得到。这样，WIM的系统就变成了车辆荷载引起的应变可知，但车辆荷载却未知的反问题。由于在役桥梁均服役一定年限以及施工同成桥之间的误差，截面EW可能已经同设计值之间发生了一定变化，该值应以现场量测的结果为主。实际操作时，此步骤也可省略，将由已知轴重的标定车通过所选桥梁的响应求出。

理论上，应变传感器所在截面的主梁弯矩可由汽车荷载所对应的影响线加载获取，称之为理论弯矩

式中，tk为依赖传感器读数频率的时间步;Ii(tk)为第i根轴重在时间步tk时对应的影响线坐标;Ai为第i根轴重;n等于总的轴数。

由于传感器读数为电子读数，其读数频率是可以设定已知的，因此可以得到

首先假设进入桥梁结构为第1根轴，Δti为第i根轴与第1根轴之间的读数时间步长差，也就是指第i根轴到达第1根轴的位置时，传感器读数次数增量;Di为第i根轴与第1根轴之间的轴距离，明显D1为0;f为传感器读数频率，单位Hz;v为车辆行驶速度，假设在桥长范围内，为一固定值。

事实上，车辆通过桥梁时，桥梁结构的响应不是静态的，而是围绕静态数值的波动。为了“过滤”掉动态响应，可以通过误差函数实现

式中，K为第1根轴上桥到最后一根轴下桥传感器期间所读数据的总次数;k为某一次读数;MMk为通过测得的应变换算出来的等效测量弯矩。

如果已知桥梁结构的影响线坐标，测量的应变真实可靠，将公式(4)代入公式(6)误差函数，就可以求解作用的各个轴重。

2 影响线标定

理论上，简支梁假设两端支撑铰接，截面弯矩影响线为两段直线;而固端梁假设梁端绝对刚接，截面弯矩影响线为两条变斜率曲线。大多数桥梁结构真实的弯矩影响线应该是介于两者之间的。Znidaric［4］在1998年的一份报告中对由影响线误差可能导致的BWIM系统的误差做了研究，便于对比，实验采用2 m跨径和32 m跨径的两组实验梁进行对比分析，研究发现:对于2 m短跨梁，无论取简支梁影响线还是固端梁的影响线对结果的影响较小;对于32 m跨梁，两种影响线计算都有可能造成较大误差。这个结论是易于理解的，如果跨径很小，直线和曲线之间坐标值差值很小，曲线变缓的程度来不及形成;而跨径较大时，其误差就会扩大。

针对这个问题，有以下思路可供解决。第一种方法:在简支梁端部增设具有一定弯曲刚度的弹簧单元，当弹簧刚度为0时为纯简支梁状态，当弹簧刚度为无穷大为固端梁状态。这种方法无法考虑结构材料的退化和弹簧刚度大小试算次数。第二种方法为直接计算法［5］。该法假设梁具有较高的一阶自振频率和较低的动力放大系数，利用不断分离每根轴及对应的已知应变来进行计算。这种方法对计算时的初应变偏离程度非常敏感，计算结果很不稳定。第三种方法为频域计算方法，这种方法对于工程师判断显得极为不便。据此，主要介绍另外一种简便的矩阵分析方法。

影响线坐标值标定首先需选定一已知轴重、轴数及总重的汽车荷载。为了便于理解，以一辆3轴、轴重分布为A1、A2、A3，距离第一根轴距分布为D2、D3的卡车分析说明求解过程。计算分3个阶段:(1)3轴未全部上桥阶段;(2)3根轴全在桥上阶段;(3)有部分轴重已下桥阶段。可假设公式(5)中读数步长Δt2=5，Δt3=8;并假设公式(6)中仪器总读数次数K=29。

则可知第一个阶段之仅第一根轴在桥上时

第一个阶段之一、二轴在桥上时

第二个阶段即所有轴均在桥上时

第三个阶段之仅一轴下桥

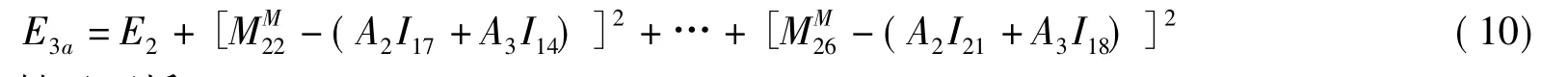
第三个阶段之一、二轴已下桥

据此，该桥梁影响线坐标I1到I21共21(K-Δt3)个未知数需要确定，可由公式(11)所需E值最小来求解，则须通过对其影响线坐标求导。限于篇幅，此处省略具体求解过程，仅给出三轴均在桥上时的通式，如下

整理(12)式写成方程形式，按影响线坐标轴升序排列，可得方程左边为

方程右边则为

依公式(12)原理，对每个待定影响线坐标求偏导后为0，共可得21个等式方程。将21个方程整理写成矩阵形式，通用公式为

代入本例的假设，为

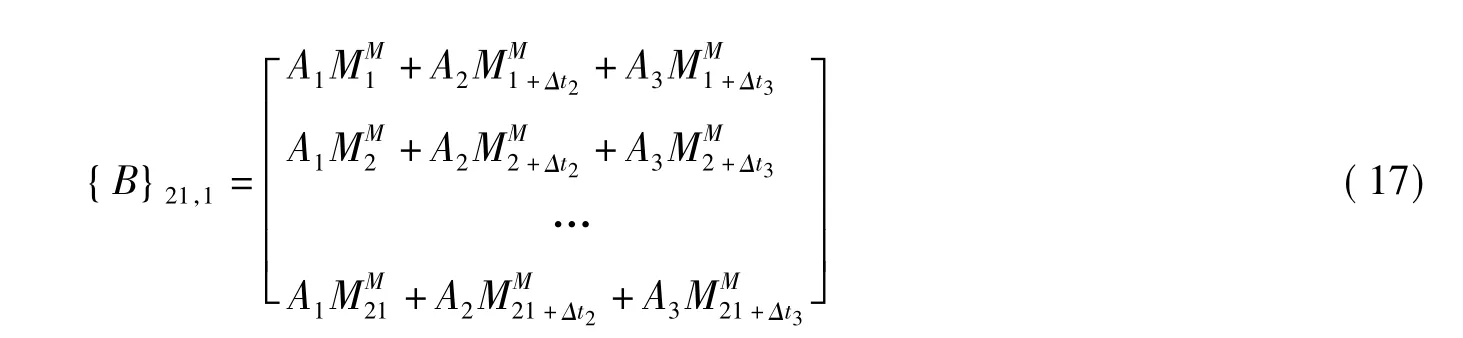
简要探讨如下:矩阵A为一稀疏对称矩阵，其中的主对角线元素均为轴重平方和，上三角中的元素也极其有规律，与公式(5)中的读数时间步长差有关;向量I为待求的影响线坐标值，其总数取决于桥长、传感器读数频率和车速;向量B长度同向量I，其中的数值取决于标重车得各轴重和测得的应变数值。

例如假设传感器采集数据频率为高频1 000 Hz，一跨径为20 m的桥梁上，15 m长的车辆车速为80 km/h通过时，也至少会采集数据900次，这样的数据对于影响线的刻度划分也是足够的。只不过对于桥跨进一步增大，方程的维数会迅速增加，求解方程的方法优劣会影响计算效率。

3 汽车荷载轴重的确定

解决了影响线坐标值问题，将其数值代入公式(6)，便可求解出汽车荷载的轴重。公式(6)为消除扰动效应的误差方程。求解轴重时，可对待求的第j根轴重进行求偏导为0，通式为

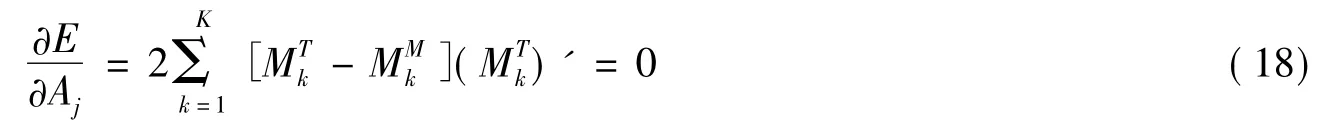
将包含轴重的公式(4)代入公式后，进一步化解可得

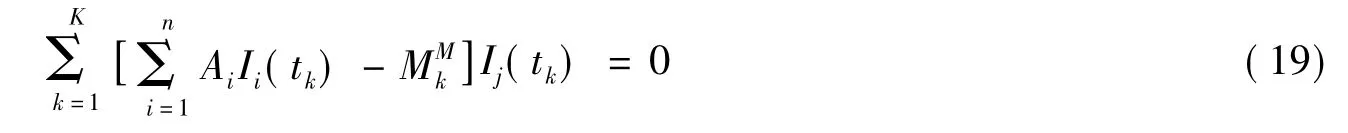
整理后，变为

由矩阵及向量运算法则可知，分离待求的轴重向量，化解后可得矩阵表达式如下

则轴重向量A为

欲求车辆总重，只需对A向量各元素求和便可。

4 结语

鉴于国内BWIM系统算法理论研究和检测设备开发的学者及科研单位较少，所以进行了相关算法的研究，推导了基于桥梁结构影响线加载的汽车荷载识别公式，该方法思路清晰，便于桥梁科研工作者及运营维护管理部门理解和改进，为下一步实验设备研制及调试奠定了良好的理论基础，同时为中小跨径桥梁开展汽车荷载调查提供了便利途径。限于篇幅，未对多车道汽车荷载相遇识别展开阐述，有待进一步研究。

［1］Snyder R，Moses F，Kriss M.Bridge weigh-in-motion system:USA，5111897［P］.1972-05-12.

［2］Moses F.Weigh-in-motion system using instrumented bridges［J］.Transportation Engineering Journal，ASCE，1979，105(3):233-249.

［3］Peters R J.A system to obtain vehicle axle weightings［C］//Proceedings 12th Australian Road Research Board Conference.Victoria:Australian Road Research Board，1984:10-18.

［4］Znidaric A，Baumgärtner W.Bridge weigh-in-motion systems-an overview［C］//Pre-Proceedings of 2nd European Conference on Weigh-in-Motion of Road Vehicles.Luxembourg:Office for Official Publications of the European Communities，1998:139-152.

［5］González A，Brien O.Influence of dynamics on accuracy of a bridge weigh in motion system［C］//Proceedings of the 3rd Conference on Weigh-In-Motion.Florida:Iowa State University，2002:13-15.