基于有限元功率流的桥梁-承轨台轨道结构振动特性研究

陈敏敏， 练松良

(同济大学道路与交通工程教育部重点实验室，上海201804)

随着城市轨道交通在我国的不断发展，其产生的振动噪声问题引起人们的广泛关注。国内外学者早已对此问题进行了大量的研究，得出了很多有意义的成果。练松良［1］综述了减振降噪型扣件和轨道结构的减振机理及其它们的使用条件，为城市轨道交通减振降噪型轨道结构的选择提供了理论指导。夏禾［2］系统阐述了城市轨道交通引起环境振动的产生机理、传播规律、对环境的影响，并探讨了一些减振措施，为进一步深入研究振动问题奠定了理论基础。

纵观前人对振动问题的研究，大多数都只是通过单值物理量(如力、加速度、速度、位移等)来衡量振动及其传递特性，但是各物理量之间的内在联系却无法具体反映出来。其实振动的传播过程，也是一个振动能量的传播过程，可以运用功率流理论从能量的角度来研究振动传播规律。功率流兼顾了力和速度的相位关系，考虑到了系统的阻抗特性，比以往的单值研究方法更具综合性。同时，输入一个系统某子结构的功率流越大，意味着该子结构越容易遭到破坏，因此可以把功率流当做一项综合指标来衡量振动的传递特性。在机械减振研究方面，功率流的运用较为广泛［3-4］，但是在轨道交通减振研究方面，功率流的运用还处于起步阶段。M F M Hussien［5］建立了地下隧道内浮置板模型，并用平均功率流来评价减振措施的有效性。谷爱军［6］采用导纳形式的功率流，建立了浮置板轨道的振动能量传递分析模型，推导了输入基础的功率流表达式，探讨了轨道参数对于减振效果的敏感性。

1 功率流理论

所谓功率流即是单位时间流过垂直于波传播方向单位面积的振动能量［6］，分为瞬时功率流和平均功率流。瞬时功率流用公式表示为

式中，Fi和Vi分别表示某一瞬时作用在结构某点的作用力和响应速度。如果作用力是一个简谐力，即Fi=|F|cosωt，产生的速度响应为Vi=|V|cos(ωt+φ)，则

在实际中，一般情况下较难得到速度和力的相位差，故功率流一般通过下面表达式得到

如果引入导纳的概念，则也可以表示成

基于导纳的功率流理论提出较早，至今仍被广泛应用，它致力于子系统输入和输出端力和速度的求解，核心在于将振源、路径和受体的动态特性分别用导纳矩阵表示，再用子结构综合法得到整个系统的振动方程［7］，但是只有少数结构能得到解析导纳，而对于大多数结构而言，导纳功率流显得无能为力。而基于有限元的功率流能克服这个缺点，从而提高了功率流理论的通用性。实践证明［8］，只要模型网格尺寸合适，用有限元方法计算得到的功率流精度能符合要求，因此在计算中采用有限元功率流。

在有限元模型中，振动能量通过各个节点传递，因此有限元功率流方法首先需要求解动力响应，得到各节点的传递力、弯矩和速度等物理量，从而进行功率流求解。对于有限元梁单元，假设有k个梁单元和评价点i相连，则某时刻流过该评价点的功率流可以表示为［9］

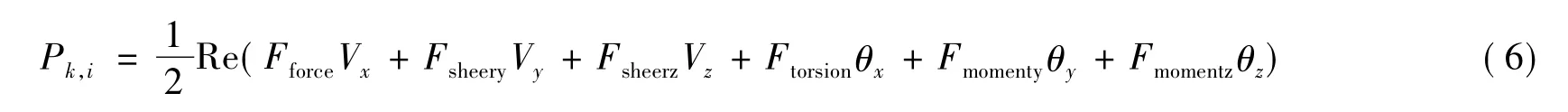
式中，Fforce，Fsheery和Fsheerz分别表示沿x轴的轴向力、x-y平面内的剪力和x-z平面内的剪力，Ftorsion，Fmomenty和Fmomentz分别表示沿x轴的扭矩、x-y平面内的弯矩和x-z平面内的弯矩;Vx，Vy，Vz，θx，θy和θz分别表示沿x、y、z方向的线速度和角速度。

2 计算模型及其参数

承轨台式轨道结构是一种常见的城市轨道交通轨道结构类型，它首次应用于上海地铁3号线，因其质量轻、高度小、结构整体性好、少维修等优点，大量应用于城市轨道交通高架线。现建立桥梁-承轨台轨道结构有限元模型，对其进行谐响应分析，求得输入各扣件处钢轨和承轨台的总功率流，进而研究其振动功率流的传递特性。

桥梁-承轨台轨道结构模型如图1所示，桥梁和钢轨全长23.4 m，扣件间距0.6 m，总共有40个扣件。钢轨采用CHN60型轨，轨间距1 435 mm，承轨台(单块)宽0.8 m，高0.3 m;桥梁宽5.2 m，高1.9 m，其中顶板厚0.25 m，腹板厚0.3 m，底板厚0.4 m、宽1.8 m。在有限元模型中，钢轨采用梁单元;扣件采用弹簧单元，用来连接钢轨和桥梁;承轨台和桥梁均采用实体单元。对有限元模型进行网格划分，考虑到模型计算频率跟网格尺寸的关系［8］，模型中钢轨的单元尺寸为0.03 m，承轨台的单元尺寸最大为0.125 m(纵向)，桥梁的单元尺寸最大为0.25 m(腹板)。划分完网格，整个模型的单元数为23 460个，节点34 390个。桥梁两端底座处和钢轨两端采用全约束，在钢轨正中间(第20～21个扣件中间)施加幅值为8 kN的简谐荷载。计算的最高分析频率为1 000 Hz，步长为0.4 Hz。

钢轨的弹性模量为210 GPa，密度为7 850 kg/m3，泊松比为0.3;承轨台与桥梁的材料密度为2 500 kg/m3，弹性模量为38 GPa，泊松比为0.167。计算时，扣件的刚度采用60 kN/mm，阻尼为75 kN·s/m。

3 振动功率流研究

3.1 振动特性

先对该模型进行模态分析，发现其前四阶垂向自振频率为10.14 Hz、22.25 Hz、45.92 Hz和47 Hz。整个系统采用Rayleigh阻尼，根据经验，Rayleigh阻尼的系数α和β分别取0.2和0.000 2，对该有限元模型进行谐响应分析，得到输入钢轨和承轨台的总的功率流，如图2所示。

图1 桥梁-承轨台轨道模型示意图

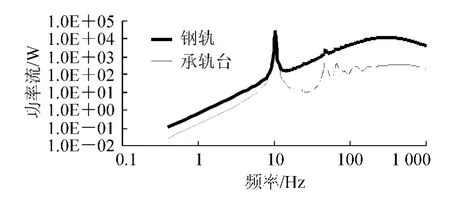
图2 输入钢轨和承轨台的总功率流

从图2中可以看出，输入钢轨的总功率流在10.4 Hz附近达到最大，为29 180 W;且输入钢轨的总功率流趋势在308 Hz之前随频率的增加而增加，在308 Hz处达到第二大值，为11 920 W，随后随频率的增加而减小。输入承轨台的总功率流随频率变化的总体趋势和钢轨的相像，但是承轨台的总功率流在500 Hz以后才开始衰减。承轨台的总功率流在10.4 Hz、47.6 Hz、66 Hz、121.6 Hz和173.2 Hz处均出现峰值，其中前两个峰值较大，分别为23 860 W和972 W。钢轨和承轨台在10.4 Hz处均出现最大的峰值，该频率正好处于整个模型的第一阶垂向自振频率附近，而承轨台的几处总功率流峰值也处于模型前几阶垂向自振频率附近，说明在模型的前几阶垂向自振频率处容易引起桥梁共振。

3.2 扣件参数对振动特性的影响

目前城市轨道交通的轨道扣件种类繁多，其扣件的参数也千差万别:扣件的刚度从普通WJ-2型扣件的60 kN/mm到高弹性VANGUARD扣件的4 kN/mm。为了研究扣件参数对桥梁-承轨台轨道结构的振动特性的影响，从扣件刚度和扣件阻尼两个方面进行分析，其中扣件刚度选用5 kN/mm、20 kN/mm、和60 kN/mm三种工况，扣件阻尼选用75 kN·s/mm、150 kN·s/mm和225 kN·s/mm三种工况。

3.2.1 扣件刚度的影响

对不同扣件刚度的三种工况进行计算，得到钢轨、承轨台的总功率流，如图3所示。

图3 扣件刚度改变对振动特性的影响

从图3可以看到，扣件刚度减小时，输入钢轨的功率流最大值在10.4 Hz频率处分别为29 180 W、33 940 W和45 290 W;此外，在230 Hz频率以下，输入钢轨的总功率流增大，而320 Hz频率以上时，总功率流减小。输入承轨台的总功率流随扣件刚度变化而变化的规律与钢轨有所不同:在46 Hz以下时，输入承轨台的总功率流随扣件刚度的减小而增大，在10.4 Hz处差值最大达到1 330 W;在46～64 Hz频率处，总功率流变化不大;在64 Hz以上时，输入承轨台的总功率流随扣件的刚度减小而减小，最大差值达105 W。总的来说，扣件刚度的降低，使得钢轨和承轨台的功率流在中低频率处增大、高频处减小。

3.2.2 扣件阻尼的影响

对不同扣件阻尼的三种工况进行计算，钢轨、承轨台的输入总功率流，如图4所示。

图4 扣件阻尼改变对振动特性的影响

从图4可以看到，随着扣件阻尼的增加，输入钢轨的总功率流在70 Hz以上频段内急剧减小，最大减小值为6 853 W;而在70 Hz以下则增大，最大增大值为548 W。对于承轨台，随着扣件阻尼的增加，总体上来说输入的承轨台的功率流有增大的趋势，最大增加了520 W，仅在47～248 Hz频段内略有减小，但是减小的值不大，最大仅为57 W。总体来看，扣件阻尼的增大能多耗散能量，因此使钢轨和承轨台的输入功率流之和减小。但是具体来说，钢轨的输入功率流在高频段内减小的幅度很大，在低频段内有所放大;承轨台的总功率流输入在中频段内稍有减小，在高频段内反而有所增加。因此扣件阻尼的增加，对于轨下结构减振的效果十分有限，但是对于钢轨的高频振动的减振效果明显。

4 结论

用基于有限元的功率流理论研究了桥梁-承轨台轨道结构的振动传递特性，并分析了扣件参数的改变对其振动特性的影响，结果发现:

(1)在模型第一阶垂向自振频率附近，钢轨和承轨台的输入总功率流值最大，且很难衰减;

(2)钢轨在308 Hz以前的输入总功率流有随频率增大而增大的趋势，308 Hz以后有减小的趋势;承轨台的总趋势与之相似，但是在模型的前几阶垂向自振频率处有峰值;

(3)扣件刚度的降低，使钢轨和承轨台的功率流在中低频处增大，高频处减小;

(4)扣件阻尼的增加，使钢轨的输入功率流在高频段大幅减小，在低频段内有所放大;使承轨台的总功率流输入在中频段内稍有减小，在高频段内有所增加，但是输入钢轨和承轨台的总功率流之和有所减小。

［1］练松良，刘加华.城市轨道交通减振降噪型轨道结构的选择［J］.城市轨道交通研究，2003，6(3):35-41.

［2］夏禾，吴萱，于大明.城市轨道交通系统引起的环境振动问题［J］.北方交通大学学报，1999，23(4):1-7.

［3］宋孔杰，孙玲玲.偏心激励作用柔性主被动隔振系统功率流特性［J］.应用力学学报，2004，21(3):89-91.

［4］宋孔杰，李新德，闫鹏.齿轮传递系统振动功率流特性研究［J］.应用力学学报，2003，20(4):93-96.

［5］Hussein M F M，Hunt H E M.A power flow method for evaluating vibration from underground railways［J］.Journal Of Sound And Vibration，2006，293:667-679.

［6］谷爱军，范俊杰.浮置板轨道竖向振动能量传递分析［J］.铁道学报，2004，26(5):125－128.

［7］宋孔杰，张蔚波，牛军川.功率流理论在柔性振动控制技术中的应用与发展［J］.机械工程学报，2003，39(9):23-28.

［8］伍先俊，朱石坚.基于有限元的功率流计算及隔振系统优化设计技术研究［J］.船舶力学，2005，9(4):138-145.

［9］杨德庆，罗放，陈静.有限元功率流落差计算方法研究［J］.噪声与振动控制，2009，29(6):127-131.