参数变化对PRC弯梁桥动力性能影响仿真分析

王洪刚， 卜建清， 付晓瑞

(1.石家庄铁道大学土木工程学院，河北石家庄050043;2.石家庄农业学校，河北石家庄050041)

0 引言

PRC弯梁桥以其线形适应性强、结构布局更加合理及美观等优点而备受设计及建造者的青睐。弯梁桥的受力特点决定了其设计与计算理论的复杂性，故对弯梁桥设计与计算理论的研究受到国内外研究者的长期关注。Lee等［1］推导了弯梁桥平面外的固有振动微分方程，并利用数值方法求得模态频率。Wu等［2］利用力和位移的关系及动力学能量方程，推得极坐标系下的曲梁单元质量矩阵与单元刚度矩阵;卜建清等［3］研究了汽车桥梁系统的参数如桥上路面不平顺、桥梁损伤、汽车参数和汽车速度对冲击系数的影响。刘华、叶见曙［4］分析了公路混凝土连续弯箱梁桥在车辆动荷载通过粗糙桥面时的动反应。现基于有限元思想和Rayleigh-Ritz变分法，推导考虑预应力效应的弯梁桥单元刚度矩阵，建立考虑预应力效应的PRC连续箱形弯梁桥模型，分析预应力、曲率半径、弯扭刚度比、约束情况、截面翘曲及车速等参数变化对PRC连续箱型弯梁桥自振特性的影响;并利用MATLAB编制了有限元程序，计算分析了各种参数变化对PRC连续箱型弯梁桥动力响应的影响。

1 PRC弯梁桥有限元单元刚度的推导

1.1 弯梁桥有限元单元刚度的推导

选取了8个单元节点位移参数:vi、vi'、φi、φi'、vj、vj'、φj、φj'。其中，vi、vj为梁段单元两端点i、j的挠度;vi'、vj'是梁段单元在两端绕径向坐标轴x的转角;φi、φj为梁段两端截面的扭转角;φi'、φj'为梁段单元两端处的扭率，详见图1所示。其中，曲率半径为R，曲梁单元夹角为dθ。

将局部坐标系的原点取在曲梁单元的中点，假设单元的长度为2λ，将曲梁两端点坐标z=－λ、z=λ代入位移函数v和φ以及其一阶导数中，并令其等于梁段单元上对应的节点位移，整理得单元位移模式

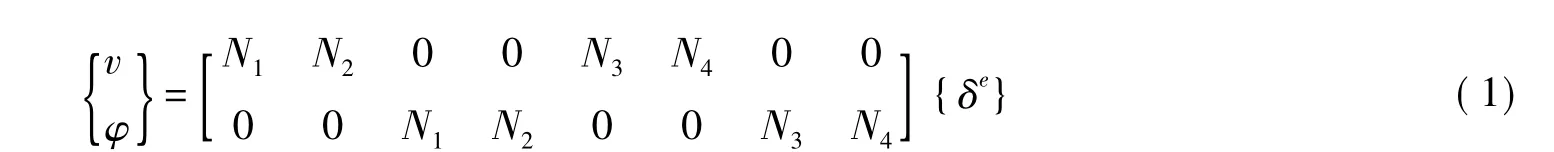
该曲梁单元的弹性刚度矩阵［5］

式中，［K1］～［K4］的展开式详见文献［5］。

1.2 考虑预应力效应对单刚修正

根据文献［6］得知，利用离散化的位移变分原理来近似求解连续系统动力问题的Rayleifh-Ritz方法，对预应力的处理方式是可行的。现利用该方法对PRC弯梁桥的单元刚度进行修正。

在预应力的作用下，结构将承受一个预应力场σ0

ij，它增加了整个系统的应变能，增加量为Vg

um为单元的位移，由于假定的单元采用一维三次两节点Hermite位移插值函数，其中单元的位移um表示为{δ}，变量为z，利用形函数表示为:{δ}={δe}，其中{δe}为单元的节点位移，因z=则式(4)改写为

将式(5)代入式(3)得

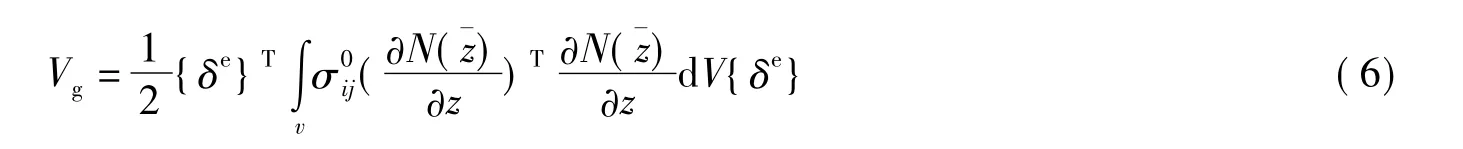
已知利用刚度表示的应变能形式为

可知，由预应力效应引起的几何刚度矩阵Kg表示为

由于采用的是一维单元，只含有坐标z，且z∈(-λ，λ)，同时假定预应力为恒定不变的Nz，则几何刚度矩阵可表示为

竖向位移v的矩阵表达式如下

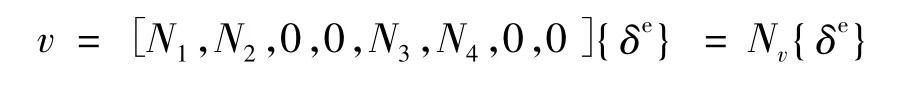
则式(10)可改写为

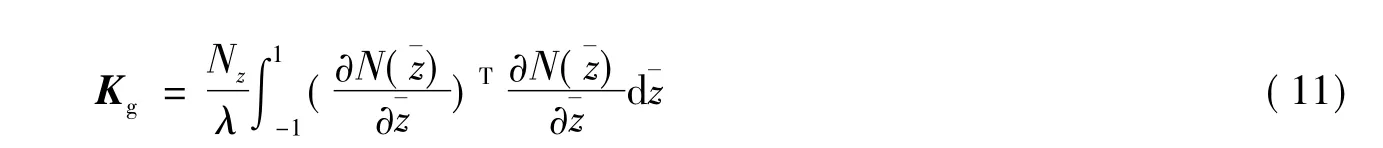
由式(11)即可求得考虑挠度v和其一阶导数对几何刚度矩阵的修正结果

根据文献［7］可知，由于此时预应力对于曲梁梁段而言相当于轴向压力(假设所取曲梁单元足够小，可视为直梁单元)，有增大竖向挠度的趋势，即对于联合(组合)刚度有减小的趋势，所以联合刚度应为原弹性刚度矩阵与几何刚度矩阵的差值。即:考虑预应力作用下的圆弧曲梁挠曲扭转的联合单元刚度矩阵［Ke］为

分析联合刚度矩阵可以看出:该刚度矩阵包含预应力Nz、弯扭刚度比EIx/GId、体现截面翘曲效应的扇形惯性矩(翘曲常数)Iw、曲率半径R和弯梁桥跨度及圆心角θ(因为弯梁的单元长度等于曲率半径与曲梁单元所夹圆心角的乘积)。由此可知，利用该修正后的刚度矩阵建立的弯梁桥有限元模型，将能够充分地反映以上各参数对PRC弯梁桥动力行为的影响，为下文的分析讨论奠定了基础。

2 PRC弯梁桥有限元模型的建立

2.1 考虑预应力效应的PRC连续箱形弯梁桥模型

弯桥梁在移动荷载作用下的控制微分方程

2.1.1 总体刚度矩阵的组集

利用推导的考虑预应力效应的单元刚度矩阵作为PRC弯梁桥动力分析中的单元刚度矩阵。利用直接刚度法进行总体刚度矩阵［K］的组集。

2.1.2 总体质量矩阵的求解及组集

对于单元质量矩阵，采用与单刚相同的位移插值函数的一致型质量矩阵

式中，［N］为与单刚相同的形函数矩阵;m(z)为质量分布函数，通常取为常数。

利用与刚度矩阵相同的直接刚度法即可组集结构的总体质量矩阵［M］。

2.1.3 阻尼矩阵的求解及组集

对于结构的阻尼矩阵［C］，采用Rayleigh阻尼，即假定

式中，α、β为瑞利阻尼常数，可根据邻近的两阶阻尼比和固有频率确定［8］。

2.2 有限元程序的编制

利用MATLAB编制有限元计算程序，该程序主要实现以下功能:

(1)完成对考虑预应力效应的单元刚度矩阵修正;

(2)组集总体刚度矩阵和总体质量矩阵;

(3)建立不考虑阻尼作用下的动力方程，计算PRC连续弯梁桥的自振特性，并通过改变结构参数，对比分析参数变化对PRC弯梁桥自振特性的影响;

(4)根据结构前两阶的模态频率及阻尼比计算结构阻尼矩阵，利用Newmark法求解移动荷载作用下结构的动力响应，并通过改变结构参数，对比分析参数变化对PRC弯梁桥动力响应的影响。

3 仿真分析

利用建立的PRC弯梁桥有限元模型，对某三跨一联的等高度PRC箱形弯梁桥的动力行为(包括自振特性和动力响应)进行分析计算;并系统地分析了PRC箱形弯梁桥的各参数对桥梁动力性能的影响。该桥跨径组合为20 m×3=60 m，支座采用两端抗扭、中间点铰支撑形式。箱梁截面形式如图2所示。采用C50混凝土;预应力钢筋采用1860号钢绞线，该预应力混凝土弯梁桥的有效预应力大小为Tr=8×104k N。

在后面的有效元数值模拟分析中，采用上述曲梁单元，C50混凝土，弹性模量为3.45×104MPa，容重为2.5 kg/m3。如果没有特别说明，则梁轴线的曲率半径为200 m。

3.1 参数变化对自振特性的影响分析

图2 箱梁截面(单位:dm)

3.1.1 预应力对自振特性的影响

仅改变弯梁桥预应力大小，保持其他所有设计参数不变的方法。分别模拟施加了六级预应力值，将设计预应力Tr分成六级:0Tr、0.2Tr、0.4Tr、0.6Tr、0.8Tr、Tr，对每种情况均计算了PRC弯梁桥的前5阶模态频率。

以零预应力作用下的弯梁桥各阶模态频率作为参考频率值，以设计预应力Tr作为参考预应力值，分析不同预应力水平作用下PRC弯梁桥的各阶频率，结果详见表1。

表1 预应力变化对PRC弯梁桥前5阶频率的影响Hz

由表1可以看出随着预应力值的增大，PRC弯梁桥的各阶自振频率值均逐步减小，说明预应力对PRC弯梁桥梁产生了一种“压缩软化”的作用，相当于降低了梁的刚度，从而使频率减小;预应力对PRC弯梁桥各阶模态频率的影响是有强弱之分的，对低阶频率的影响要强于对高阶频率的影响，对第一阶频率影响最大。

3.1.2 曲率半径对自振特性的影响

仅改变该弯梁桥半径的大小，保持其他所有设计参数不变。将弯梁桥设计曲率半径取值范围设定为30～500 m，对每种情况均计算了结构的前6阶模态频率。图3给出了第1、2和5、6阶模态频率随半径变化情况。

通过对比分析图3可知，对于其他设计参数均未改变的PRC弯梁桥的模态频率随曲率半径的变化趋势分别为:随半径的增加而增大和随半径的增大而减小两种情况;且通过分析可知，当半径大于200 m时，预应力混凝土弯梁桥的模态频率变化幅度减小，并趋同于直线梁桥的模态频率。

图3 曲率半径变化对模态频率频率的影响

3.1.3 弯扭刚度比对自振特性的影响

仅改变该弯梁桥弯扭刚度比的大小，保持其他所有设计参数不变，来研究弯梁桥弯扭刚度比对结构自振特性的影响，以求寻找出一定的规律性。将设计的弯扭刚度比分别设定为:0.5、1、5、10、100，对每种情况均利用PRC弯梁桥有限元模型计算了结构的前10阶模态频率。模态频率随弯扭刚度比的变化情况详见图4所示。

图4 不同弯扭刚度比下各阶频率变化情况

从图4可以看出，对于不同弯扭刚度比下的结构模态频率变化情况。即:采用不同的弯扭刚度比时，对结构的低阶频率影响较小，对于高阶频率的影响较大，且随着频率阶数的增加影响越明显。主要原因为随着弯扭刚度比的增大，截面的扭转效应相对变小，接近于直线梁桥;同时，当抗弯刚度增大时，桥梁的弯曲效应将会减小，一定程度上消减了弯扭耦合作用的影响。通常在曲率半径较小时，要求截面的抗弯刚度和抗扭刚度比较接近为宜，即取值范围在［0.5～1.5］;而文献［9］从静力学的角度分析得知，对于箱形弯梁桥的弯扭刚度比的合理取值范围为［0.5～5］;综合弯梁桥动力行为与静力行为分析结论可得，PRC箱形弯梁桥的合理弯扭刚度比范围宜取为［0.5～1.5］。

3.1.4 约束情况对自振特性的影响

仅改变该弯梁约束情况，保持其他所有设计参数不变，来研究弯梁桥约束情况对结构自振特性的影响。约束情况分为图5所示的两种情况。不同约束情况下的前十阶模态频率计算结果详见表2。

从表2可以看出，对于不同的约束情况，PRC弯梁桥的模态频率发生了变化。即:采用抗扭支撑普遍增大了结构的模态频率，且主要增大的是结构的扭转振动频率，因为扭转约束增加了结构的扭转刚度。从而可知，当连续梁中间支座采用抗扭支撑形式时比点铰支撑的抗扭刚度大，提高了结构的弯扭刚度比，从而可使该类弯梁桥的弯扭刚度比处于了合理范围，使得结构的内力和动力特性均更加趋于合理。

表2 不同约束方式的模态频率值Hz

3.1.5 截面翘曲对自振特性的影响

采用考虑截面翘曲和不考虑截面翘曲两种情况，保持其他所有设计参数不变的方式。利用已有的PRC弯梁桥有限元模型进行计算，求得两种情况下的各阶模态频率变化情况，结果详见图6所示。其中:f1代表考虑截面翘曲影响下的各阶频率值，f2代表不考虑截面翘曲影响下的各阶频率值。

图5 曲线连续梁桥约束方式

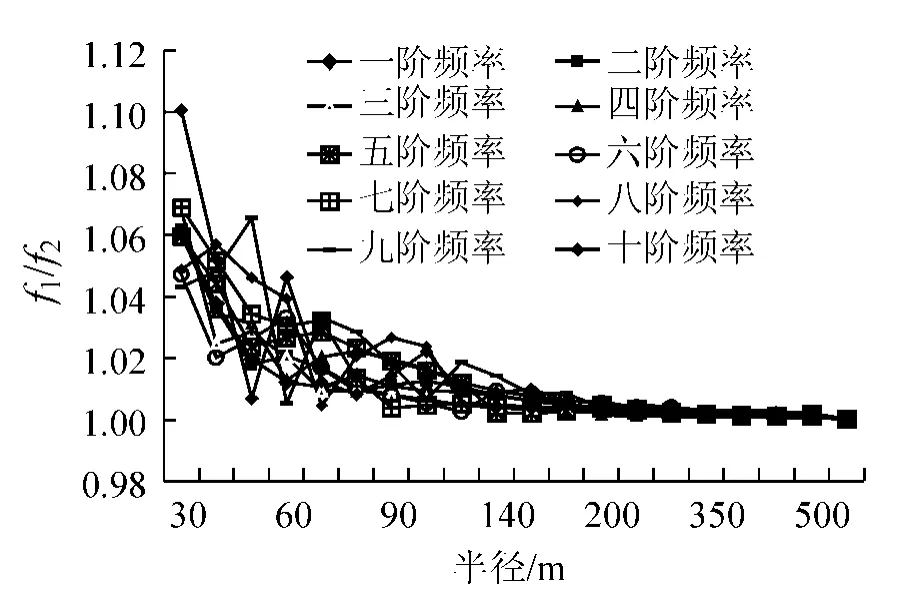
图6 截面翘曲对弯梁桥自振频率的影响

从图6可以看出，截面翘曲对PRC弯梁桥的各阶频率都有影响，考虑截面翘曲影响时，结构的模态频率将有所增加，这是因为截面翘曲增大了弯梁桥的刚度所致;且随着半径的增大对于模态频率的影响效果逐渐变小，且当半径大于250 m之后，翘曲对于模态频率的影响趋于稳定。

3.2 不同参数对桥梁动力响应的影响

采用直接积分法中的Newmark法计算移动荷载作用下PRC弯梁桥的动力响应。忽略桥面不平整对荷载的干扰，并设定其为匀速移动荷载，大小恒定为300 kN，并以20 m/s的速度匀速行驶在该弯梁桥上，计算分析不同参数对PRC连续箱形弯梁桥动力响应的影响。

3.2.1 预应力对动力响应的影响

保持其他所有设计参数不变，而模拟计算了在依次施加同3.1所述的六级预应力水平情况下，移动荷载通过PRC弯梁桥时桥梁的动力响应。

为了使对比分析结果更加明显，在此重点将该PRC连续箱形弯梁桥中跨的跨中在有无预应力作用下的动力响应时程曲线进行对比分析，详见图7。

由图7可知，预应力对于PRC弯梁桥的位移、速度、加速度响应均有影响，且预应力水平越高，对弯梁桥动力响应的影响越明显。在有无预应力两种工况下，三跨连续梁中跨跨中动力响应时程曲线的变化规律是相同的，即时程曲线出现波峰和波谷是同时的，而且对振动加速度、速度和位移的影响规律是一致的。由单刚推导结果可知，预应力改变了弯梁桥的刚度，从而影响了结构的动力响应。可见，预应力与PRC弯梁桥的动力响应有着密切的联系。

3.2.2 曲率半径对动力响应的影响

对PRC弯梁桥的中跨跨中在不同曲率半径情况下的动力响应进行对比分析。不同曲率半径下中跨跨中的位移和加速度响应对比分析结果详见图8和图9。

从图8和图9中可以看出，不同曲率半径下的动力响应受到了曲率半径变化的影响。当半径较小时，动力响应随着半径的增加而变化剧烈，而当半径在达到200 m后，动力响应开始趋于稳定。可见，对于该类PRC弯梁桥而言，半径选在200～500 m之间较为合理。

图7 有无预应力情况下桥梁中跨跨中的动力响应

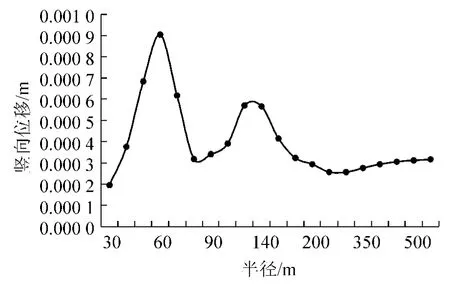
图8 不同曲率半径下中跨跨中位移动力响应

图9 不同曲率半径下中跨跨中加速度动力响应

4 结论

采用数值模拟方法分析了参数变化对PRC弯梁桥动力性能的影响，结果表明:

(1)PRC弯梁桥的预应力与结构的自振特性和动力响应关系密切，故在确定预应力水平时，不但要考虑结构的受力情况与耐久性，也应该考虑其对动力特性的影响;

(2)当半径增大到200 m后，PRC弯梁桥的动力行为(模态频率与动力响应)与直线桥梁接近，宜将半径选在200～500 m之间，并应综合考虑影响选线的其它因素确定具体曲率半径值;

(3)不同的弯扭刚度比对结构的低阶频率影响小于高阶频率，且PRC弯梁桥的合理弯扭刚度比宜取在［0.5～1.5］之间;

(4)抗扭支撑与点铰支撑相比增大了结构的模态频率，且主要增大了扭转振动频率;

(5)截面翘曲增大了PRC弯梁桥的刚度，且随着半径的增大其影响逐渐变小，当半径超过250 m后，翘曲对于模态频率的影响将趋于稳定。

另外，在动力行为影响因素中没有考虑桥面不平顺情况、横隔板位置及其数量、车辆荷载变速行驶及双向行车情况，因此还需做进一步的深入研究。

［1］LEE B K，OH S J，PARK K K. Free vibrations of shear deformable circular curved beams resting on elastic foundation［J］. International Journal of Structural Stability and Dynamics，2002，2( 1) : 77-97.

［2］］WU J S，CHIANG L K. Out-of-plane responses of a circular curved Timoshenko beam due to a moving load［J］. International Journal of Solids and Structures，2003，40: 7425-7448.

［3］卜建清，娄国充，罗韶湘.汽车对桥梁冲击作用分析［J］.振动与冲击，2007，26(1):52-55.

［4］刘华，叶见曙.公路混凝土弯箱梁桥的动反应［J］.东南大学学报，2006，36(2):278-282.

［5］吴西伦.弯梁桥设计［M］.北京:人民交通出版社，1990.

［6］GERADIN M，RIXEN D.Mechanical Vibration:Theory and application to structural dynamics［M］.New York:John Wiley and Sons，1994:645-690.

［7］克拉夫R，彭津J.结构动力学［M］.北京:高等教育出版社，2006.

［8］黄海东，向中富.基于预应力损失识别的连续刚构桥内力计算方法［J］.公路交通科技，2008，25(6):71-76.

［9］吴六政.曲线梁桥设计中几个关键技术研究［D］.成都:西南交通大学建筑与土木工程学院，2004.