轴承故障诊断与故障预测方法

2011-07-25张星辉康建设刘占军李志勇

轴承 2011年1期

张星辉，康建设，刘占军，李志勇

(军械工程学院 a.装备指挥与管理系；b.训练部，石家庄 050003)

轴承的故障是一个从正常到失效逐步演化的多状态过程，这些状态不能直接观测，但可以通过外部设备测量得到的信号来反映状态的变化。故障诊断和预测就是通过对测量得到的信号进行分析，提取反映设备故障特征的特征向量，应用模型来识别设备的健康状态，并对未来一段时间内的状态进行估计，或预测设备的剩余使用寿命。文献[1]将隐Markov模型(HMM)应用于故障诊断和预测，并提出了基于HMM的故障诊断和预测框架。文献[2]将轴承状态分为正常、点蚀、浅层剥落、深层剥落和失效5个状态。但轴承在实际运行过程中，这些状态之间的时间间隔都很长，诊断得出的结果只能粗略反映轴承的退化量，不能很好地预测剩余寿命的值。如果HMM划分的状态过多，模型本身的计算复杂度随状态数的增加呈指数级增长，并且需要大量的样本进行训练。而层次隐Markov模型(HHMM)可以对轴承的状态进行分层表达，进一步将5个状态表达为5个HMM，可以更精确地反映轴承的退化过程，提高剩余寿命预测的精度[3-4]。

1 HHMM的基本原理

HHMM是HMM的一种扩展形式，是结构化的多层随机过程，能够用来表述时序数据的等级结构特性。如图1所示，在一个HHMM模型中，顶层状态由子状态组成，当且仅当子状态结束时顶层状态才转移到下一个状态。

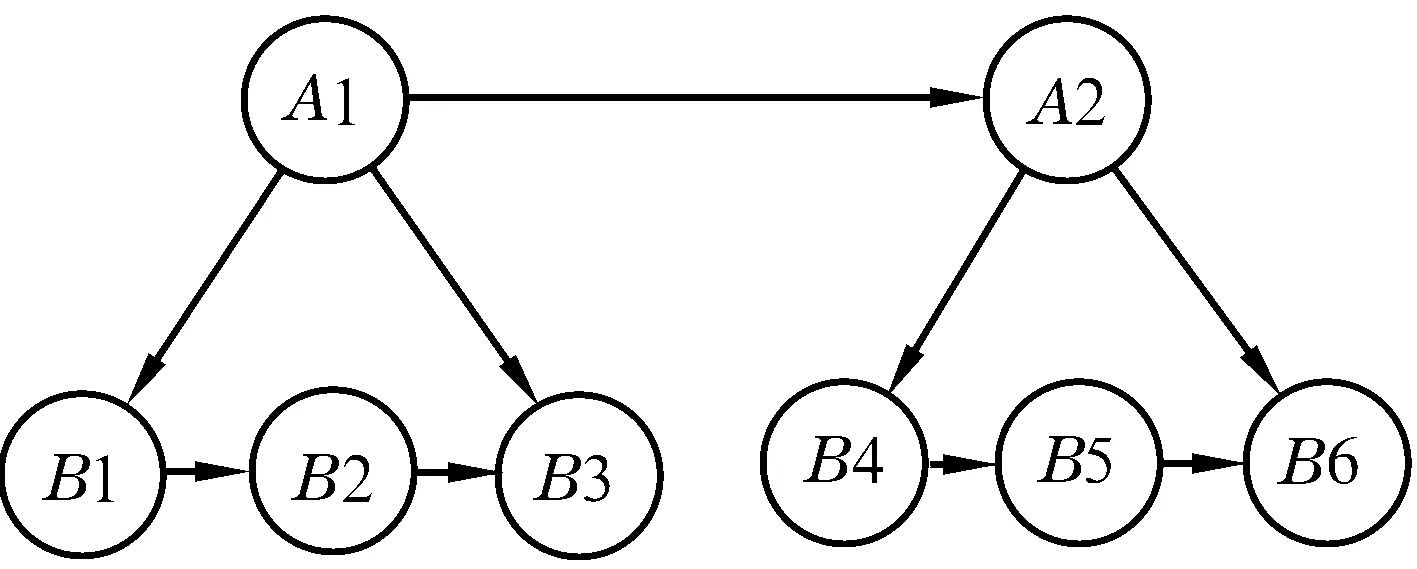
图1 状态分层表示(A—顶层状态; B—子状态)

1.1 HHMM模型描述

(2)模型中与隐状态对应的m个观测值为O={o1,…,om} 。

(4)观测值概率矩阵：Bqd={bqD(k)}，其中，bqD(k)=P(ok|qD)是状态qD产生观测值ok的概率。这样HHMM可以表述为[4]：λ={λqd}d∈{1,…,D}={{Aqd}d∈{1,…,D},{∏qd}d∈{1,…,D},{BqD}}。

1.2 HHMM转化为DBN

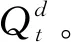
图2 HHMM的DBN表达

2 轴承故障诊断和故障预测框架

2.1 故障诊断

故障诊断的任务是根据轴承运行过程中监测到的各种信号，识别轴承当前的健康状态。在此主要是对振动信号进行分析，然后用HMM进行故障诊断。应用HMM进行诊断的过程如图3所示，分为模型训练和模型识别两个阶段。其中矢量量化的目的是对提取的连续特征信号进行量化编码，以满足离散HMM的输入观测值序列为离散整形数值的要求。

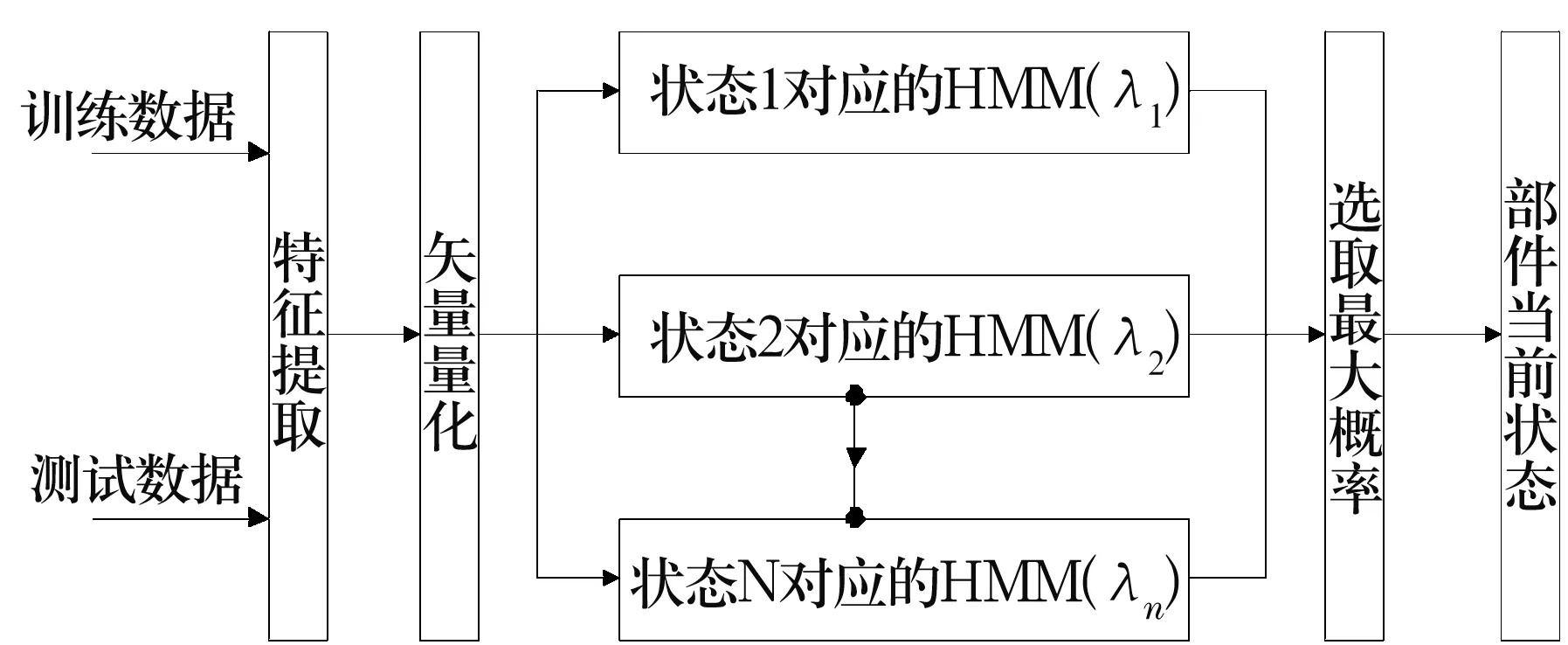
图3 基于HMM的故障诊断

对于模型识别，则需要为代表每种故障状态的特征向量训练一个HMM。将测试信号经特征提取和矢量量化后形成的序列与代表故障状态的特征向量进行对比，特征最相近的一个即是当前的故障状态。

2.2 故障预测

故障预测是根据退化过程中的征兆信息，在判断当前故障严重程度的基础上，利用状态转移关系信息，预测故障的演化趋势或估计剩余使用寿命。轴承的退化过程可以用一个两层HHMM进行表示，顶层代表轴承的正常及4种损伤直径，底层则代表相邻两个损伤直径之间的发展过程，也可称其为子状态。利用HHMM进行故障预测的过程如图4所示，分为模型训练、状态识别和预测3个阶段。(1)模型训练：收集轴承退化过程中N个不同健康状态的样本数据，经特征提取和矢量量化后形成观测值序列，分别训练出N个用于状态识别的HMM模型。同时，利用整个退化过程数据训练出一个全寿命周期模型。(2)状态识别：对未知测试数据经特征提取和矢量量化后形成待识别的观测值序列，分别计算HMM产生此观测值序列的概率，输出概率最大的模型所对应的状态就表示部件当前的健康状态。(3)故障预测：根据当前状态识别结果，代入用Bayes网络工具箱[6]建立的HHMM模型，预测轴承在离散时间点处于每个状态的概率，那么各时刻轴承处于最后一个状态的概率即为故障率。

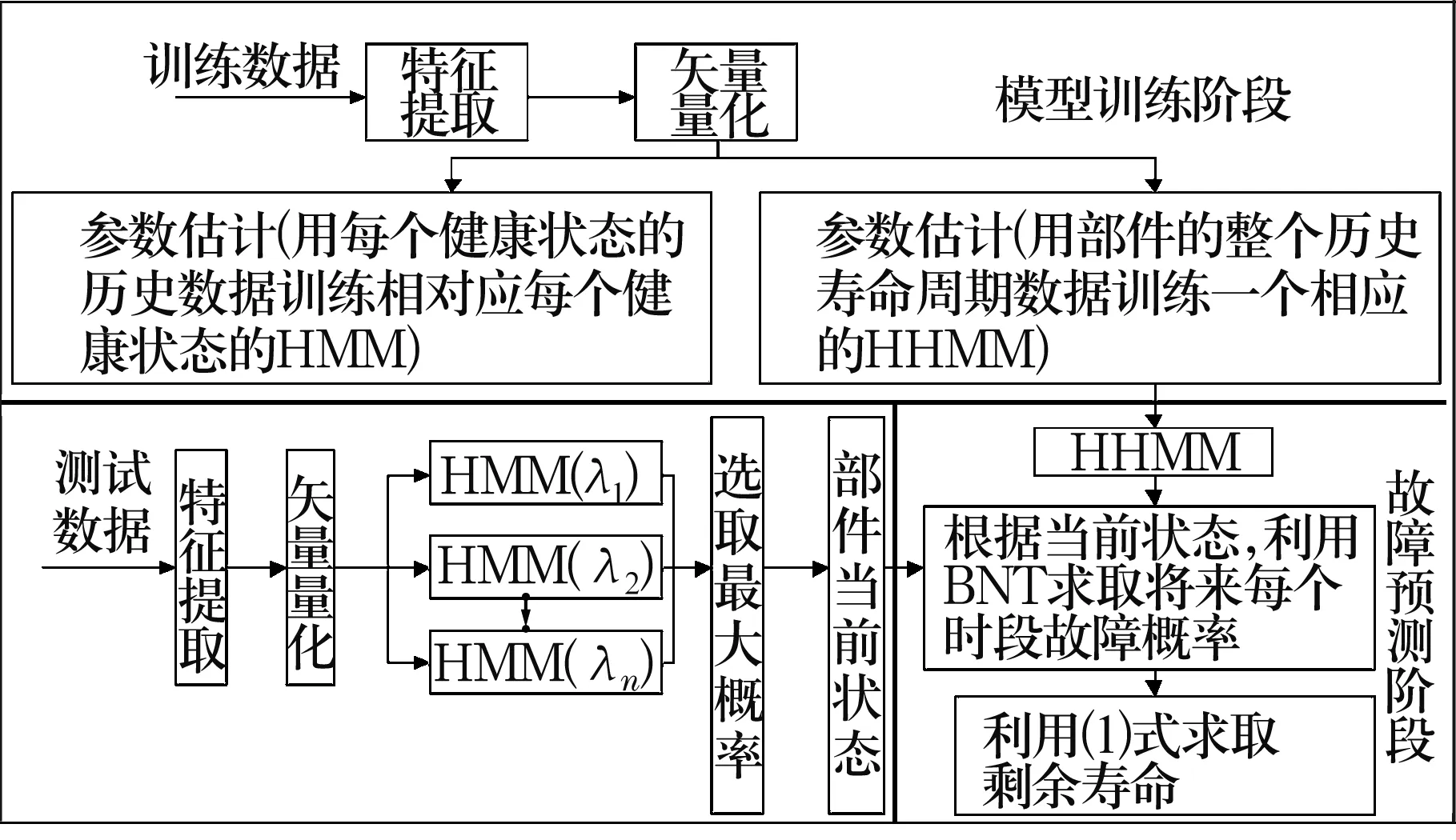
图4 基于HHMM的故障预测

平均寿命为

(1)

式中：λ(t)为故障率。为了方便求取寿命，需要等时间间隔采集数据。

3 应用案例分析

3.1 滚动轴承故障诊断

由于滚动轴承试验条件暂时缺乏，采用美国Case Western Reserve University电气工程实验室的滚动轴承故障模拟试验台的试验数据[7]进行研究分析。

试验台由电动机、扭矩传感器/译码器、功率测试计和电子控制器组成，待检测轴承支承电动机的转轴，驱动端轴承型号为6205,风扇端轴承型号为6203。

加速度传感器安装在带有磁力基座的机架上，风扇端和驱动端的轴承座上方各放置一个加速度传感器。振动加速度信号由16通道数据记录仪采集。风扇端轴承故障采样频率为12 kHz，驱动端轴承故障采样频率为12 kHz和48 kHz。功率和转速通过扭矩传感器/译码器测得并手动记录。采用驱动端转速为1 797 r/min，采样频率为12 kHz得到的内沟道故障数据进行验证。损伤直径分别为0.177 8，0.355 6，0.533 4和0.711 2 mm。

3.1.1 特征提取

采用小波包分析建立一个能够表征系统状态的特征向量。对振动信号进行4层小波包分解，提取从低频到高频8个频率成分的信号特征。然后对小波包分解系数进行重构，提取各频带范围的信号。

(2)

式中:xjk为重构信号Sij的离散点的幅值(j=0，1，…，7；i=1, 2, 3 ,4；k=1，2，…，n)。由于系统出现故障时对各频带内信号的能量有较大的影响，因此，以能量为元素构造一个特征向量。特征向量T由32个元素组成。当能量较大时，Eij通常是一个较大的数值，在数据分析上会带来一些不方便的地方。因此，对特征向量T进行改进，即对特征向量进行归一化处理，

(3)

令T′=T/E，向量T′即为归一化后的向量。

3.1.2 矢量量化

采用Lloyd方法进行矢量量化[8]。利用matlab中的lloyds和quantiz函数可以求得T′的整形量化编码序列，作为HMM的输入观测值序列。

3.1.3 模型训练

将轴承内沟道故障数据进行特征提取和矢量量化后，分别用40组代表各损伤直径的数据训练4个HMM模型，每个模型隐状态数取2，观测状态数取4，当前、后两次迭代输出的对数似然概率值之差小于0.000 001时，认为模型收敛，停止迭代。

3.1.4 故障诊断

将每组样本的观测序列输入到训练好的模型中，分别计算4个HMM产生此观测序列的对数似然概率值。设4种损伤直径所对应的观测值序列分别为O1，O2，O3，O4，计算结果如图5所示。图5中横坐标为样本编号，纵坐标为对数似然概率值，即lgP(O|λ) 。图中‘*’表示损伤直径为0.177 8 mm的对数似然概率值，‘+’表示损伤直径为0.355 6 mm的对数似然概率值，‘×’表示损伤直径为0.533 4 mm的对数似然概率值，‘○’表示损伤直径为0.711 2 mm的对数似然概率值。通过比较概率值的相对大小来确定样本数据所对应的健康状态，对数似然概率值最大的HMM对应的损伤直径即为当前轴承的损伤状态。从图中可以看出，前3种状态的40组数据全部判断正确，最后1种状态的40组数据有4组判断不准确。总地来说，结果比较理想。

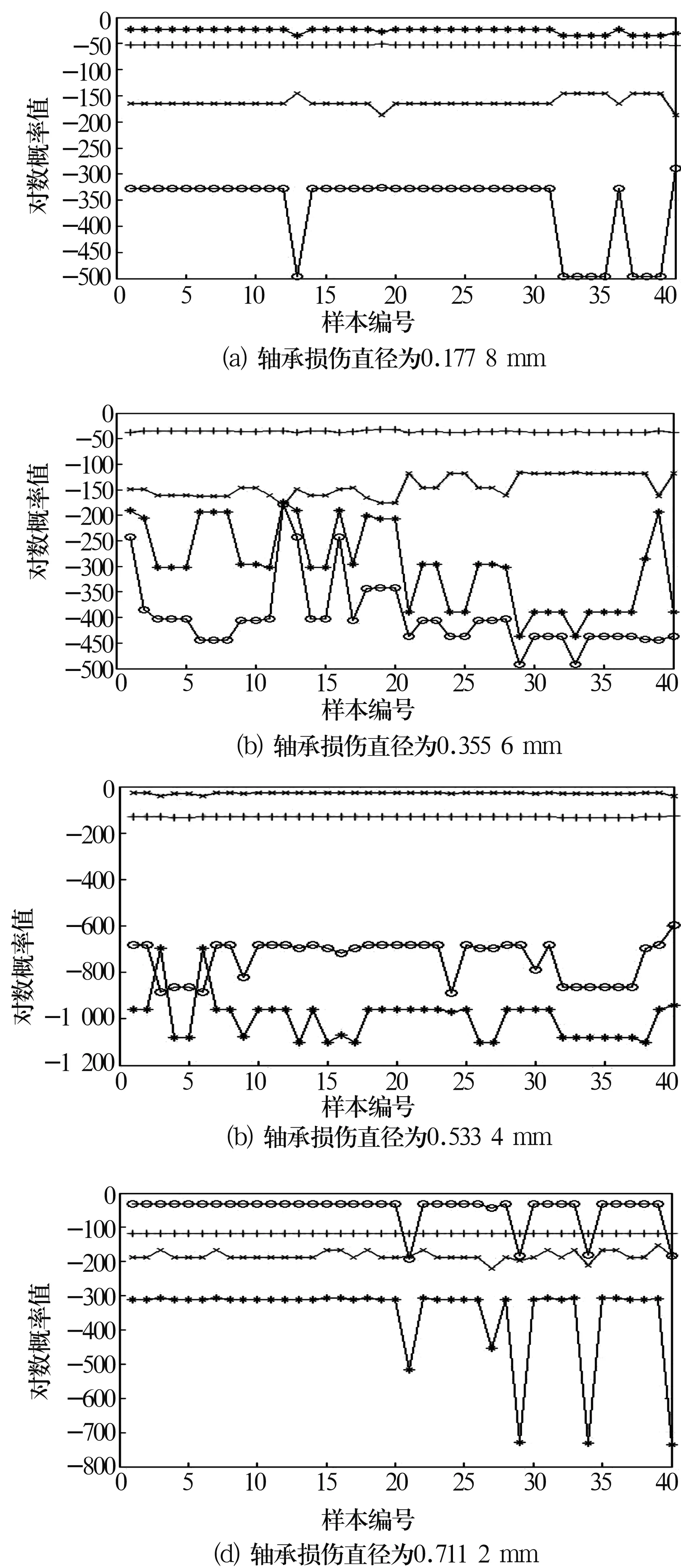
图5 4种损伤直径下的识别结果

3.2 滚动轴承故障预测

由于试验条件所限，很难获得轴承全寿命数据。以轴承单点损伤为例，损伤是逐渐扩大且加深的。Case Western大学振动试验台设置的4种单点损伤直径正好可以描述轴承单点损伤的发展过程。用3次样条插值对数据进行插值处理，以增加样本数据量。插值后的数据为损伤直径每增大0.025 4 mm为一组数据，共28组数据，定义损伤直径0.711 2 mm为故障。这样就可以建立轴承的HHMM故障预测模型，模型将轴承按照损伤直径划分为5个状态，即正常，0.177 8，0.355 6，0.533 4和0.711 2 mm。相邻两个状态之间又划分为7个子状态，这样可以更详细地表达故障的程度。模型由Bayes网络工具箱中的函数建立，用20组样本数据训练模型，假设试验时每隔10 h采集一次数据，那么轴承的寿命为280 h。然后就可以根据当前获取的数据进行故障诊断，得出当前的状态，然后对以后的状态进行预测。假设轴承现在的单点损伤直径为0.177 8 mm，将矢量量化后的数据输入模型可以诊断出当前状态并预测将来各个时刻轴承处于各个状态的概率，如表1所示。表中“0”时并不是指全新的轴承开始运转的时刻，而是将开始对轴承进行检测的时刻定义为“0”时。

表1 轴承在不同时刻处于各状态的概率表

由于数据量比较大，表1中只列出了间隔为50 h，从50～750 h的数据。图6所示为故障率变化曲线。因为各个时刻的故障率是离散值，所以对故障率曲线进行拟合，得到故障率的表达式为

图6 故障率曲线

λ(t)=p1t9+p2t8+p3t7+p4t6+p5t5+p6t4+p7t3+p8t2+p9t+p10,

(4)

式中：p1=-1.979 9×10-24;p2=5.656 4×10-21;p3=-5.208 5×10-18;p4=1.397 5×10-16;p5=2.984 1×10-12;p6=-2.193 5×10-9;p7=6.744 5×10-7;p8=-8.494 5×10-5;p9=3.937 9×10-3;p10=-0.046 304。

由(1)式可得到MTTF=243.174 4 h，误差值为33.174 4 h。