弹性储能装置中平面涡卷弹簧的有限元分析
2011-07-25冯恒昌王璋奇
段 巍,冯恒昌,王璋奇
(华北电力大学 能源动力与机械工程学院,河北 保定 071003)
风力发电是典型的随机性和间歇性能源,影响电网稳定运行,给风电上网带来困难.储能系统具有动态吸收能量并适时释放的特点,能有效弥补风电的间歇性和波动性的缺点,从而改善风电场输出功率的可控性,提升电网的稳定性水平.现有的储能方式主要包括物理储能、电磁储能、电化学储能和相变储能,其中物理储能又称为机械储能,包括抽水蓄能、压缩空气储能和飞轮储能[1-9]等.机械储能方式具有储能容量大、效率高、成本较低和无污染等优点.平面涡卷弹簧是机械行业中广泛使用的一种弹性元件,受载时产生较大的弹性变形,将机械能或动能转化为变形能,卸载后弹簧的变形消失并恢复原状,将变形能转化为机械能或动能.鉴于平面涡卷弹簧所具有的能量储存和转换特点,本文提出了基于平面涡卷弹簧(以下简称涡簧)的机械式弹性储能-发电系统方案,并针对方案中储能装置的关键零件平面涡卷弹簧建立了力学模型和有限元模型,分析了涡簧的扭转变形、横截面上的应力分布、固有频率和前20阶振型,研究成果为储能装置的优化设计、储能密度的计算提供了有力依据.
1 弹性储能-发电系统方案
基于平面涡卷弹簧的机械式弹性储能-发电系统方案如图1所示.当储能时,控制系统控制双馈电机工作于电动机状态,并控制断路器合闸,来自电网的电能驱动电机运行,通过传动系统使涡簧储能装置中的涡簧拧紧,涡簧即以弹性变形能的形式将能量储存起来,完成电能到弹性变形能的转换;之后,控制系统控制断路器断开,并控制涡簧维持锁紧状态,即存储状态,直到接收到1个能量释放的控制信号;当释能时,控制系统控制双馈电机工作于发电机状态,并控制锁紧的涡簧释放弹性能,通过传动系统带动双馈电机发电,同时控制电机并入电网,从而实现涡簧弹性变形能到电能转换的能量释放过程.
涡簧储能装置是弹性储能-发电系统的核心组成部分,为了提高储能密度,该装置可由若干个涡簧储能箱并联组成,如图2所示.每个涡簧储能箱包括箱体1、制动机构2、涡簧3、涡簧主轴4以及支撑主轴的一对轴承5组成,其中平面涡卷弹簧是涡簧储能箱的核心元件,其设计质量的好坏直接影响到储能-发电系统的可靠性和安全性.
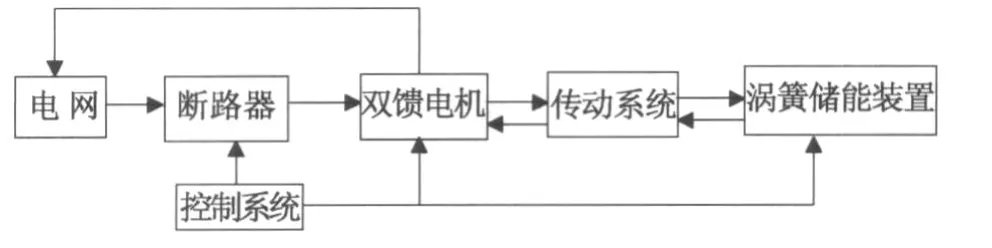
图1 弹性储能-发电系统方案示意图Fig.1 Diagram of elastic storage energy and power generation system
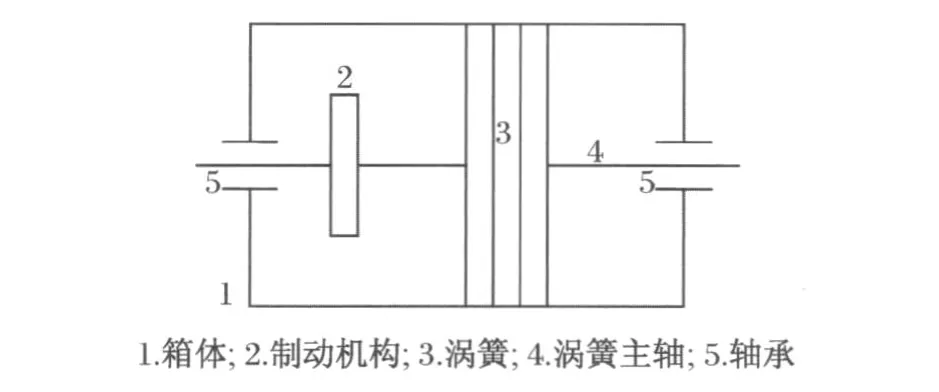
图2 涡簧储能箱简图Fig.2 One flat spiral spring energy box
由于涡簧的几何形状复杂,很难直接采用解析方法得到每一圈涡簧的应力分布及固有频率,因此本文采用有限元数值分析方法,通过建立涡簧的力学模型和有限元模型,对其进行有限元应力分析和模态分析,得到涡簧的最大变形量和截面应力及其在受到扭矩作用下发生的变形.
2 涡簧的力学模型
平面涡卷弹簧是一种使用细长的弹簧材料绕制成平面螺旋线的弹簧.其一端固定,另一端作用扭矩后,涡簧产生弯曲弹性变形,从而使涡簧在自身平面内产生扭转.其所受到的扭矩T和发生变形后变形角φ的特性曲线如图3所示,其中图3a表示的是无弹簧盒情况下的特性曲线,OA段表示当涡簧刚刚受到扭矩作用而开始卷紧时,涡簧各圈依次发生变形,该段为线性变形,特性曲线为直线;AB段表示直至最后一圈发生变形,涡簧才在全长内发生变形,该段的特性曲线可近似为直线;BC段表示继续加载时,涡簧各圈逐渐卷紧从而导致其特性曲线急剧变化为渐增型,但是由于弹簧圈卷紧使得心轴的转数小于工作转数,所以,可以认为在B点时弹簧已经完全卷紧,因此BC段为弹簧的非工作部分.图3b表示有弹簧盒情况下的特性曲线,涡簧放进弹簧盒后,大部分弹簧圈紧压在簧盒上,当涡簧卷紧时,弹簧圈逐渐离开簧盒,此时的特性曲线亦为曲线,如图3b中O1A段所示;在AB段时,涡簧在全长内工作,所以特性曲线为线性;BC段时和无弹簧盒时情况一样.
由图3可以看出,当涡簧处在自由状态O点时,有簧盒和无簧盒的工作部分完全一致,只是达到工作部分时涡簧的空转圈数不同,因此在弹簧的工作部分即AB段,涡簧变形角φ的大小与扭矩T成正比,即

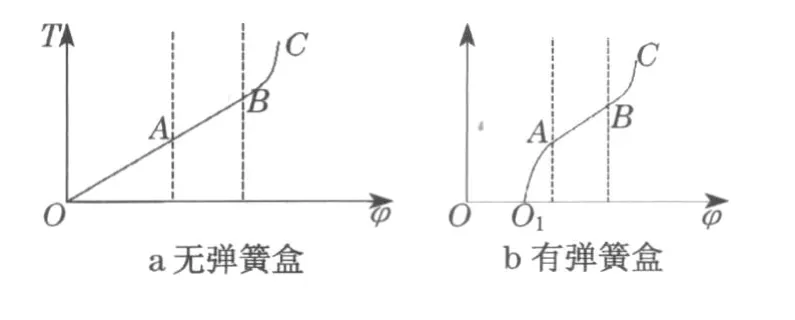
图3 涡簧的特性曲线图Fig.3 Characteristic curve of flat spiral spring
式中:K为涡簧的刚度.
设涡簧尾端采用固定方式,固定点为A点,该点距涡簧中心O的距离为r,当轴上作用扭矩T时,A点处将受到力矩T1、切向力Pt和径向力Pr的作用,如图4所示.沿弹簧长度s取长度无限小的ds弹簧单元体,则此单元内的弹簧变形能dU为

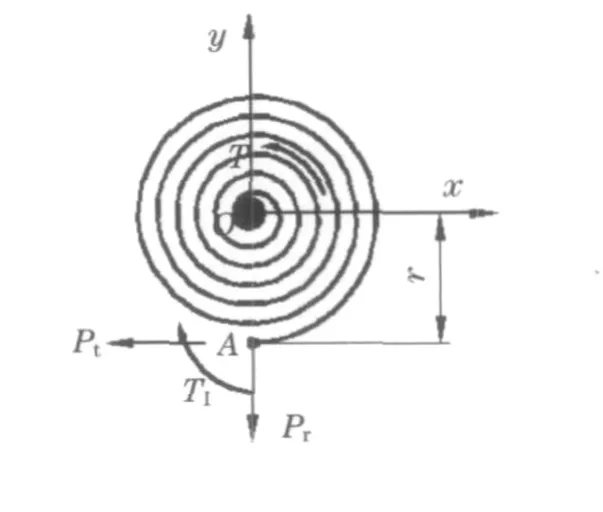
图4 涡簧的受力分析简图Fig.4 Force analysis of flat spiral spring
式中:E为材料的弹性模量;I为材料截面的惯性矩.
当涡卷弹簧的有效长度为l时,沿曲线全长积分可得弹簧的变形能U为
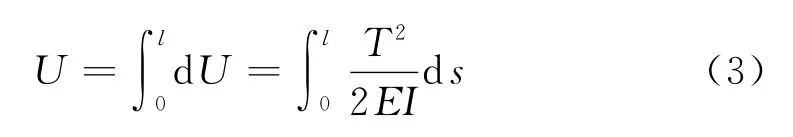
在轴上作用扭矩T后,涡簧在全长各个截面内都承受大小相同的力矩,并且与轴上作用的力矩相等,所以涡簧的变形角为

由式(1),(4)可以得到弹簧的扭转刚度为

此外,由式(3),(4)可以得到涡簧储能公式的另一种表达方式为

如果用变形圈数n表示变形角的大小,则φ=2πn,涡簧的工作圈数为

本文根据JB/T 7366—1994《平面涡卷弹簧设计计算》[10]进行涡簧的尺寸选择和性能计算.该标准仅适用于厚度为0.5~4mm,宽度为5~80mm的矩形截面材料的涡簧.本文选择厚度为4mm、宽度为80mm的涡簧进行计算,其材料选择为55CrMnA弹簧钢带,得到涡簧的设计数据:弹簧的横截面尺寸为80mm×4mm,弹簧工作长度为60m,最大输出转矩为264.48N·m,最小输出转矩为132.24N·m,芯轴直径为0.1m,松卷时的转数为28,有效工作转数为24.
3 涡簧有限元模型
3.1 模型描述
为了保证涡簧有良好的外形结构,本文采用阿基米德螺旋线绕制而成的涡簧作为研究对象,该涡簧的厚度为4mm、宽度为80mm、长度为60m,其材料性能如表1所示.考虑到该涡簧的长度与横截面积之比较大,在建模时将涡簧等效成曲梁,采用节点法并使用BEAM188单元进行有限元建模.该模型包含6 000个节点和5 999个单元,涡簧模型如图5所示.

表1 涡簧的材料性能Tab.1 Material properties of flat spiral spring
3.2 边界条件的确定
在储能装置中涡簧是放在涡簧盒当中的,其中尾端固定在簧盒上,顶端固定在芯轴上.进行加载时,在涡簧的尾端施加约束,在顶端施加转矩,如图6所示.
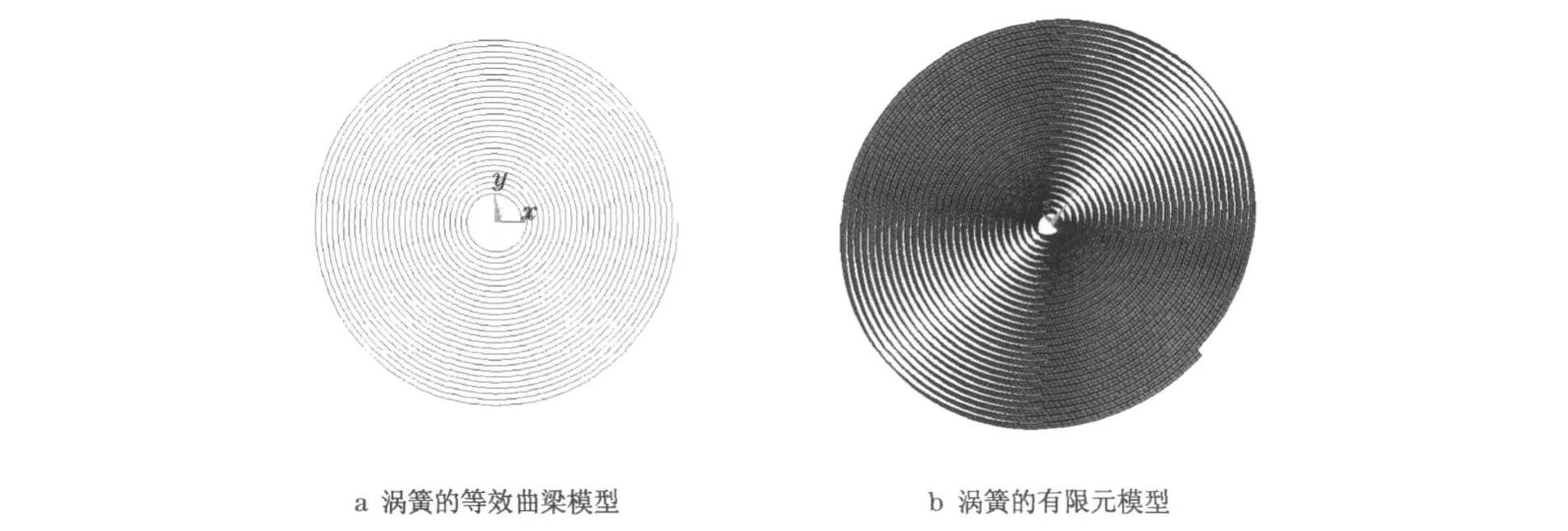
图5 涡簧模型Fig.5 Model of flat spiral spring
4 涡簧的有限元分析
国内外学者开展了钢板弹簧[11]、碟形弹簧[12]及片弹簧[13]的有限元分析,而本文所研究的平面涡卷弹簧的应力分析是大变形非线性问题,考虑到其受应力影响较小,材料的变形属于弹性变形,因此可采用一般的线性问题分析方法,不需要特别定义非线性材料,在进行有限元分析时只需设定大变形选项即可.
4.1 应力分析
图7为在施加大小为264.480N·m的扭矩后涡簧的形状变化图.由图可以看出:涡簧在变形过程中存在偏心,这就使涡簧卷紧时在弹簧圈互相接触的地方存在摩擦.为了减小摩擦,保证弹簧圈同心移动,可以通过改变弹簧尾端固定方式来实现.
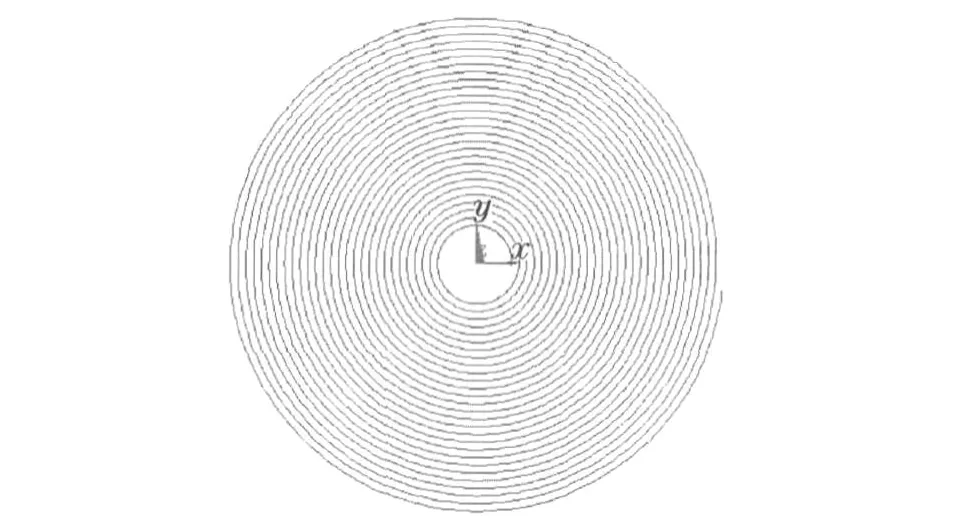
图6 边界条件Fig.6 Boundary conditions
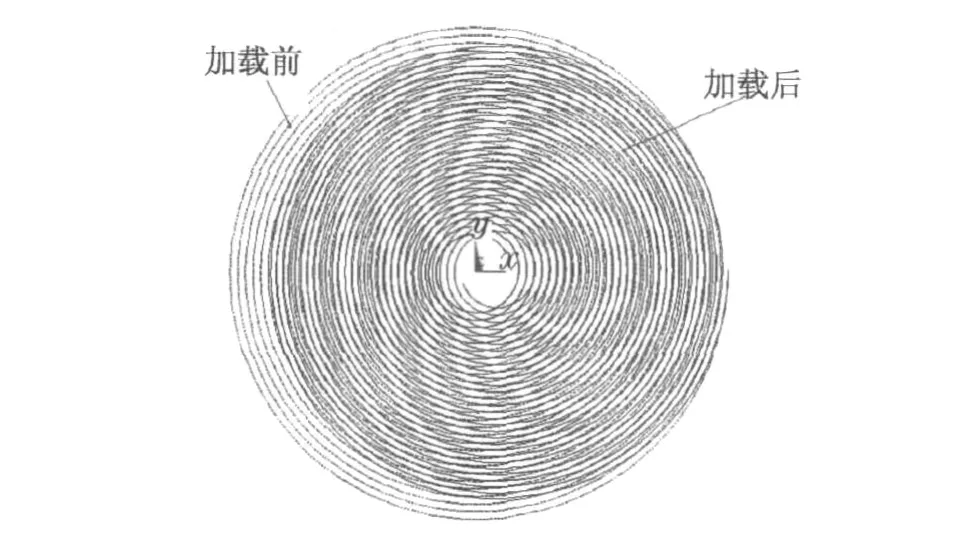
图7 加载后形状变化图Fig.7 Deformation under loading
图8为涡簧的节点位移矢量图,该位移矢量表示的是节点位移的矢量和.由图可以看出:节点最大矢量位移发生在旋紧后的第22—26圈,大小为589.564mm.此外,涡簧的圈数也由于被旋紧而发生了相应的变化,由最初的28圈变为30圈.
涡簧在扭矩条件下,仅在x方向受到拉应力,其余方向应力皆为0.由于每一圈的应力情况基本类似,本文只给出了涡簧的第28圈节点应力图,如图9所示.由图可以看出:涡簧在发生弯曲的过程中,最大应力值发生在涡簧的上下两个表面,其最大值为106.114MPa,涡簧的应力呈现明显的层状分布.
4.2 模态分析
本文所研究的涡簧模态分析是在涡簧尾端施加约束的条件下进行的.在进行模态分析时,变形的阶数设置为20,由于涡簧的圈数很多,而且存在空转,部分阶数的变形很难显示出来,图10给出了10阶具有明显特征变形的涡簧振型,表2给出了相应阶数的固有频率.
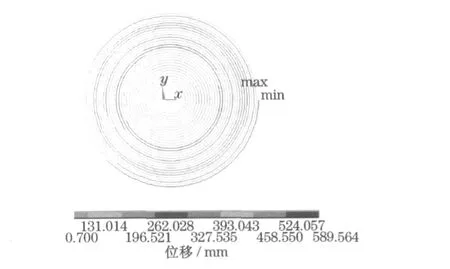
图8 涡簧的节点位移矢量图Fig.8 Nodal vector displacement of flat spiral spring

图9 涡簧第28圈节点应力图Fig.9 Nodal stress of the 28th coil

图10 涡簧的部分变形阶数Fig.10 Vibration modals in some orders
由图10可以看出,涡簧是从中心部分开始依次发生变形,直到最后一圈发生变形为止涡簧才在全长范围内产生变形;从1—8阶,由于存在空转,涡簧几乎不发生形变,直到9阶才开始有明显的变形;到15阶时,完成第一次变形,而从16阶振型开始,涡簧在第一次变形的基础上开始进行第二次变形;在变形过程当中,随着变形量的增大,涡簧的固有频率也在发生明显变化,如表2所示.

表2 涡簧部分阶数的固有频率Tab.2 Inherent frequencies of 10orders modal
5 结论
本文提出基于平面涡卷弹簧的机械式弹性储能-发电系统方案,以储能系统核心元件涡簧为研究对象,建立了涡簧的力学模型和有限元模型,确定了涡簧的几何参数;对涡簧进行了应力分析,得到了涡簧的最大变形量和截面应力分布规律;对涡簧进行了模态分析,得到了涡簧的固有频率和振型,分析了固有频率和变形之间的关系.研究成果为涡簧的优化设计、储能密度的计算提供了有力依据.
[1]贾宏新,张宇,王育飞,等.储能技术在风力发电系统中的应用[J].可再生能源,2009,27(6):1-6.
JIA Hongxin,ZHANG Yu,WANG Yufei,et al.Energy storage for wind energy applications[J].Renewable Energy Resources,2009,27(6):1-6.
[2]GEORGESCU M,BAROTE L,MARINESCU C,et al.Smart electrical energy storage system for small power wind turbines[C]∥12th International Conference on Optimization of Electrical and Electronic Equipment.Piscataway:IEEE,2010:1192-1197.
[3]MOHOD S W,AWARE M V.Energy storage to stabilize the weak wind generating grid[C]∥2008Joint International Conference on Power System Technology and Power India Conference.New Delhi:Inst of Elec and Elec Eng Computer Society,2008:1-5.
[4]靳建鼎.新能源形势下储能元件及其装备的发展机遇[J].电子工艺技术,2009,30(5):258-260.
JIN Jianding.Development opportunities of energy storage component and its equipment for new energy[J].Electronics Process Technology,2009,30(5):258-260.
[5]张文亮,丘明,来小康.储能技术在电力系统中的应用[J].电网技术,2008,32(7):1-9.
ZHANG Wenliang,QIU Ming,LAI Xiaokang.Application of energy storage technologies in power grid[J].Power System Technology,2008,32(7):1-9.
[6]VESZPREMI K,SCHMIDT I.Flywheel energy storage drive for wind turbines[C]∥7th International Conference on Power Electronics and Drive Systems.Bangkok:Institute of Electrical and Eletronics Engineers Inc,2007:916-923.
[7]陈星莺,刘孟觉,单渊达.超导储能单元在并网型风力发电系统的应用[J].中国电机工程报,2001,21(12):63-66.
CHEN Xingying,LIU Mengjue,SHAN Yuanda.Application of super conducting magnetic energy storage system-smes in wing power system of network forming[J].Proceedings of the CSEE,2001,21(12):63-66.
[8]唐西胜,武鑫,齐智平.超级电容器蓄电池混合储能独立光伏系统研究[J].太阳能学报,2007,28(2):178-183.
TANG Xisheng,WU Xin,QI Zhiping.Study on a stand-alone PV system with battery/ultracapacitor hybrid energy storage[J].Acta Energiae Solaris Sinica,2007,28(2):178-183.
[9]ABOUL-SEOUD T,JATSKECICH J.Improving power quality in remote wind energy systems using battery storage[C]∥Canadian Conference on Electrical and Computer Engineering.Niagara Falls:Inst of Elec and Elec Eng Computer Society,2008:1743-1746.
[10]姜膺,张英会,万桂香,等.平面涡卷弹簧设计计算[M].北京:机械工业出版社,1994.
JIANG Ying,ZHANG Yinghui,WAN Guixiang,et al.Design calculation of flat spiral spring[M].Beijing:China Machine Press,1994.
[11]曲昌荣,巢凯年.钢板弹簧的有限元分析[J].轻型汽车技术,2005(10):15-19.
QU Changrong,CHAO Kainian.Finite element analysis of leaf spring[J].Light Vehicles,2005(10):15-19.
[12]兰洪波.碟形弹簧模态分析[J].机械工程师,2010(10):33-35.
LAN Hongbo.Modal analysis of disc spring[J].Mechanical Engineer,2010(10):33-35.
[13]GUO Hong,JING Dan,HAO Chengdi,et al.Optimal design and finite element analysis of few-leaf-spring[C]∥International Conference on Computer,Mechatronics,Control and Electronic Engineering.Piscataway:IEEE,2010:303-306.
