Modeling and Simulation of Aerial Dispersion on Piston Dispersal Mechanism

TAO Ru-yi(陶如意)，WANG Hao(王浩)，HUANG Bei(黄蓓)

(School of Energy and Power Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China)

Introduction

As one of the key technologies of cluster munition system，some dispersing methods are developed，including aerodynamic force dispersion，kinetic energy dispersion，mechanical force dispersion，blasting dispersion and propellant gas dispersion.

Propellant gas dispersing，which submunition is dispersed by the high temperature and pressure gas，has been applied widely because the submunition muzzle velocity and its distribution is controllable in this way.The propellant gas dispersion includes piston dispersion，gas-filled bag dispersion，and bellows dispersion.The paper focuses on the piston dispersing that works with the propellant gas in the chamber.

The piston dispersing is to use the propellant gas to push the submunitions and piston.At present，the most attention is paid to the static piston dispersing process.As a matter of fact，both the submunition and the carrier are pushed by the propellant gas in the piston dispersing process，so it is important to study aerial piston dispersing.The aerial dispersing interior ballistic process is studied and a novel model is proposed in this paper.The piston maximum travel limit and the effect of reaction force on the cluster munition are explored to the internal ballistic model for the first time.The initial external ballistic parameters model is developed.

1 Operational Principle of System

The piston dispersal mechanism is composed of ejector cartridge，combustion chamber，cluster munition shell and piston，as shown in Fig.1.The working process of piston dispersal mechanism is as follows:firstly，powder is ignited by a triggering signal from control system when cluster munition arrives at the dispersing location;the pressure in the ejector cartridge increases with the powder burning，and the propellant gas and burning powder enter into the combustion chamber after the seal cover of ejector cartridge is broken by the gas;and then the piston and submunition are pushed by gas，meanwhile，the reverse-ejection move towards the right about of submunition.Finally，the submunition moves slowly until it is separated from the cluster munition completely because of the resistance，and the piston is quiescent relative to the carrier after it arrives at travel limit.

Fig.1 Schematic drawing of the piston dispensing device

2 Mathematical-physical Model

2.1 Interior Ballistic Model

2.1.1 Basic Assumption［2］

1)Burning model of ejection powder

The ejection powder is entirely ignited as soon as the igniting charge is burnt out.The burning process of ejection powder meets the geometric burning law.Its burning rate is an exponential function of average pressure in the combustion chamber.

2)Propellant gas model

Ingredient freezing and Alfred Nobel equation should be followed by propellant gas，and the propellant gas and the unburnt propellant grain are distributed uniformly.

3)Movement model of submunition

Before the piston arrives at the travel limit，the speed of submunition in the cabin is as same as that of piston.There is a resistance only after the submunition arrives at the travel limit.

4)Movement model of reverse-ejection

The reverse-ejection movement begins while the piston moves due to the effect of reaction force，and it is pushed by the propellant gas before the piston arrives at the travel limit.The reverse ejection is affect by a resistance only after the submunition arrives at the travel limit.

5)Secondary work and energy loss

Energy loss and secondary work are revised by calculation coefficient of secondary work.

2.1.2 Foundation of Coordinate System

In order to study the movement of submunition and reverse-ejection，a virtual cluster munition concept is introduced here，which its archetype is the cluster munition before dispersing.Submunition and reverseejection are dispersed from the end and head of virtual cluster munition，respectively，and the moving state of virtual cluster munition is identical to that of cluster munition before dispersing.Based on the concept of virtual cluster munition，the coordinate system of virtualclustermunition axisis founded and namedO'εη1ζ1，where the origin is the center of mass of the virtual cluster munition，and the axe of virtual cluster munition is selected asO'εaxis that it points to the warhead of cluster munition［3］，as shown in Fig.2.In this paper，shell body axis coordinates of virtual cluster munition is the reference system of the interior ballistic model.

Fig.2 Shell body axis coordinates of virtual cluster munition

2.1.3 Mathematical-physical Model

According to the processes of powder burning and interaction，the interior ballistic process is divided into four periods:the first period is that powder is burnt until the seal cover is broken.The second period is from the end of the first period to the point when the piston and reverse ejection start to move.The third period is from the end of the second period to the point when the piston arrives at the travel limit.The last period is from the end of the third period to the moment that all the submunitions are dispersed from the shell.

Since the different reaction forces are applied on the submunition and reverse-ejection before and after the piston arrives at the travel limit，the different modeling methods are used to study the model with the maximum travel limit of piston.

1)Before the piston arrives at a maximum travel

In this phase，the piston starts to move and the submunition and reverse-ejection are pushed by propellant gas.

(1)Model of powder burning

The burning rate law is:

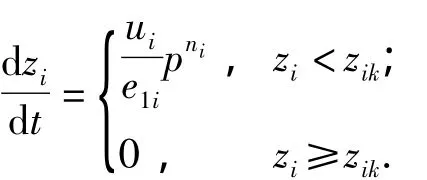
Function of shape is:

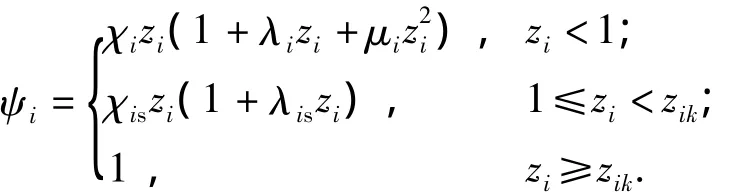
wheree1is one half of the initial powder arc thickness;zis the percentage of burnt thickness;uis the burning rate constant;nis pressure exponent of burning rate;pis mean pressure;ψis the percentage of burnt mass;χ，λ，μare the shape characteristic parameters of powder;χs，λsare the splitting point of powder;zkis the relative burnt thickness after completely burning;suffiximeans theith powder.

(2)Movement equation of submunition

whereSis the effective area on the piston pushed by gas;pis the average pressure in the combustion chamber;pbis the resistance when a submunition moves;φbis the virtual mass coefficient;lis the travel limit of piston;vis the moving velocity of submunition;andMis the total mass of piston，submunition and padding，that is

wherempis mass of piston;mfjis mass of thejth padding;mbjis mass ofjth submunitions;Kis the remaining submunitions in the cabin.Assuming thatNis the total set number of submunitions in the cabin which the coding starts from the submunitions adjacent to the piston:1，2，3…K，K+1…N，M0is the total mass of dispersed submunitions and padding:

(3)Movement equation of reverse-rejection

whereSreis the action area of reverse-ejection;φreis the virtual mass coefficient of reverse-ejection;preis movement resistance;lreis the travel distance of reverse-ejection.

(4)Equation of gas state

whereSlais the cross section area of launching tube，|l－lre|is the length increment of free volume after movement of submunition and reverse-ejection;τis relative temperature，τ=T/T1;fis powder force;mpois mass of powder;Vψis the initial free volume of ejector cartridge and combustion chamber:

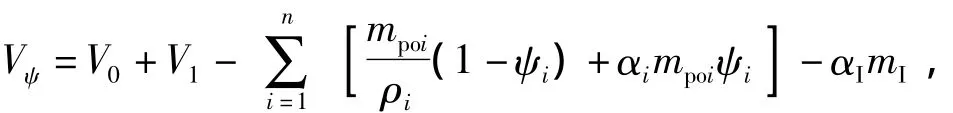
where，V0is the combustion chamber volume of expulsion cartridge;V1is the initial volume of combustion chamber;ρis the density of powder;αis the covolume of powder;nis the category number of loading powder;αIis the covolume of igniting charge，andmIis the mass of igniting charge.

(5)Equation of energy conversation

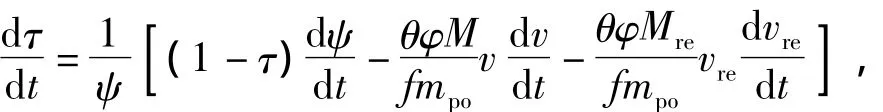
where，θ=k－1，kis specific heat ratio;φis coefficient of second work;parametersψ，f，mpoare determined by the concentration.

2)After piston arrives at the travel limit

As soon as the piston arrives at the travel limit，the piston collides with reverse-ejection，then they move together.According to conservation of momentum，we have

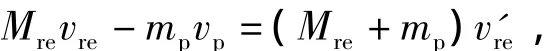
wherevreandvpare the velocities of reverse-ejection and piston when the piston arrives at the travel limit.

Since the submunition and reverse-ejection are not pushed by the propellant gas after piston arrives at the travel limit，they move under resistance.Their initial velocities arevpandv're，respectively.

The burning model of power is same as that before the piston arrives at the travel limit.

(1)Movement equation of submunition

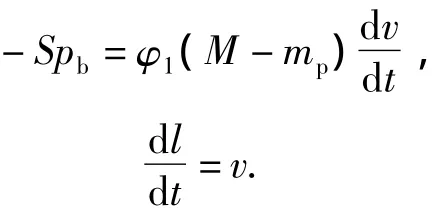
(2)Movement equation of reverse-ejection

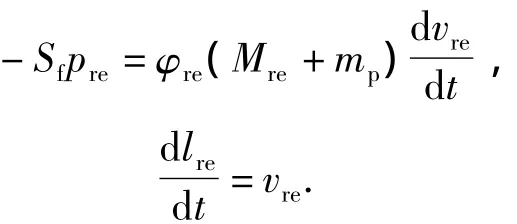
(3)Equation of gas state

wherelpmaxis the travel limit of piston.

(4)Equation of energy conversation

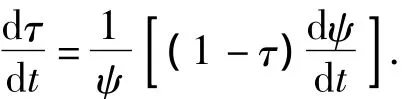
2.2 Calculation of Initial Parameters of Submunition External Ballistics

It is important how to calculate initial velocity，firing angle and firing direction，that are the initial parameters of submunition external ballistic.Now，a submunition initial external ballistic model is established.

It is supposed that the axial direction of submunition is parallel to the shell body axis of cluster munition，and the attitude of cluster munition hold the line during dispersing.

2.2.1 Velocity and Position of Submunition Relative toO'εη1ζ1

Theith submunition ofjth round inkth segment is studied in the coordinate systemO'εη1ζ1.γis the azimuth angle ofith submunition relative to the axisO'η1.Since its circular velocity direction is atγ+90°，so its velocity can be expressed by

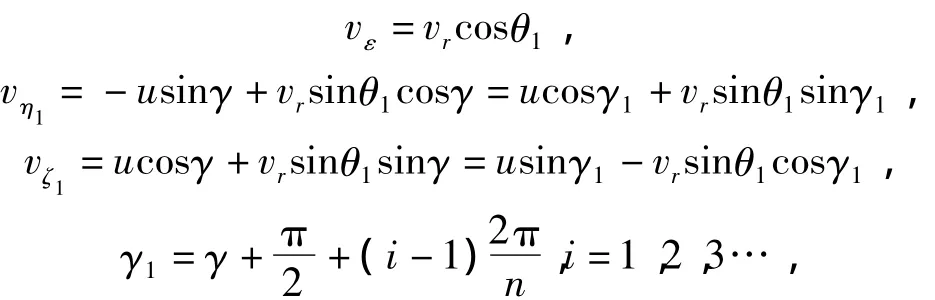
wherevris the dispersing velocity inO'εη1ζ1，θ1is the angle between the dispersing velocity and the axis of cluster munition，which is named the guide angle of guide tube in the piston dispersal mechanism;nis the number of submunitions;uis the transverse circular velocity of submunition，u=rω，whereωis the rotation velocity of cluster munition when it arrives at the dispersal location，ris distance from submunition centroid to the axis of cluster munition，

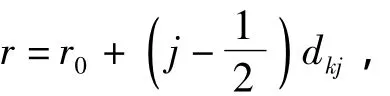
wherer0is the radius of center frame，jis thejth round of thekth segment，anddkjis the diameter of thejth round of thekth segment.

The position of the submunition inO'εη1ζ1is given by

wherentis total segment number，lbandrbare the radial travels of submunition parallel and vertical to the axis，respectively.

2.2.2 Transfer Matrix FromO'εη1ζ1to Ground Coordinate SystemO'xyz

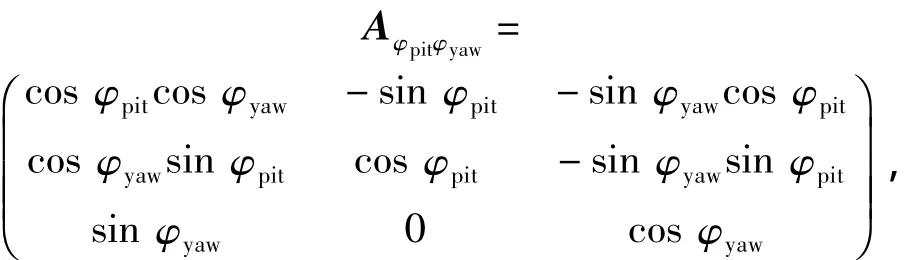
whereφpit，φyaware the elevation and azimuth oscillation angles，respectively.

2.2.3 Calculation of Initial Parameters of Submunition External Ballistic

As discussed in Section 2.2.1 and 2.2.2，when the submunition is dispersed completely，its movement equation inO'xyzis denoted as follows

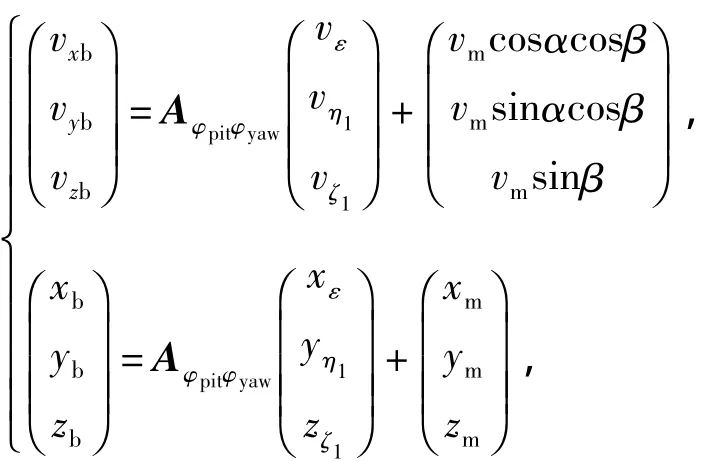
whereαandβare the dip angle of trajectory and the deflection angle of cluster munition at dispersing location，respectively;vmis the velocity of virtual cluster munition inO'xyzwhen a submunition departs the cabin，andxm，ymandzmare the positions of virtual cluster munition inO'xyzwhen a submunition departs the cabin.

Furthermore，a 6DOF ballistic model of cluster munition and a particle ballistic model of submunition can be established to simulate the whole ballistic trajectory of cluster munition in conjunction with the calculation model mentioned above.

3 Numerical Simulation and Analysis

In this section，a dispersing system of a certain cluster munition is simulated，which its guide tube is without oriented angle［4］，and its submunitions are dis-persed backwards.Its structure and loading parameters are shown in Tab.1.

3.1 Simulation and Analysis of Static Dispersing

In the experiment of static dispersing，the cluster munition is fixed，and the submunition is pushed by piston which is pushed by propellant gas of powder.The static dispersing process can be simulated by the said dynamic model that sets the mass of reverse-ejection to be a maximum.

Tab.1 System structure and loading parameters

Powder burning percentage，powder gas pressure curve，submunition velocity history and submunition stroke diagram of simulation are shown in Fig.3 － 6，respectively.The conclusions of these figures are given as follows:

Fig.3 Powder burning percentage

Fig.4 Powder gas pressure curve

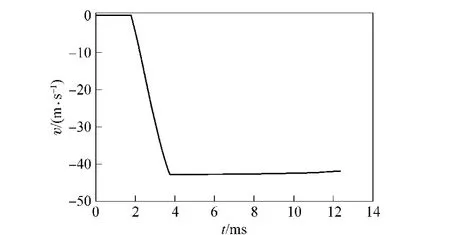
Fig.5 Velocity history of submunition

Fig.6 Submunition stroke diagram

After the powder is burnt for 0.091 ms，the pressure of propellant gas is enough to break the film，and then the propellant gas and the remaining powder rush into the combustion chamber.After the powder is burnt for 1.64 ms，the propellant gas can push the piston to move，and the submunition starts to be pushed by piston.After a lapse of 2.34 ms，the pressure is the highest in the combustion chamber and decreases gradually from then on.After a lapse of 3.60 ms，the velocity of submunition is －42.79 m/s，and the volume of combustion chamber and the pressure produced by propellant gas no longer increase or decrease because the powder is burnt completely after a lapse of 3.32 ms.The departing velocity of the first dispersed submunition segment is －42.77 m/s.Simulation velocity is compared with experimental velocity(－40 m/s)which is in good agreement with the data，so the static dispersing model can be expressed by the dynamic model with maximum reverse-ejection mass.

3.2 Simulation Result and Analyses of Aerial Dynamic Dispersing

In this section，the external ballistic trajectory of cluster munition is computed by 6DOF model，of which the parameters are shown in Tab.2.The trajectory dip angleαis － 65.54°，the trajectory deflection angleβis 3.545°，the swing angleφpitis － 65.55°，the de-flection angleφyawis 3.70°，the rotation speedωis 1 217.93 rad/s.

Tab.2 Initial parameters of submunition exterior trajectory(in earth axes)

Fig.7 －10 show the simulation results of internal ballistic trajectory of dynamic dispersing model.As shown in Fig.7 and Fig.8，all of submunitions are not dispersed，but the piston arrives at the travel limit with velocity of－23.0 m/s and the velocity of reverseejection is 38.20 m/s after a lapse of 2.98 ms from powder burning.Because it needs 3.87 ms to burn the powder completely，the elapse time is more than the time of that the piston arrives at the travel limit.As a result，the pressure in the combustion chamber continues to increase after an elapse of 2.98 ms until the powder is burnt completely.

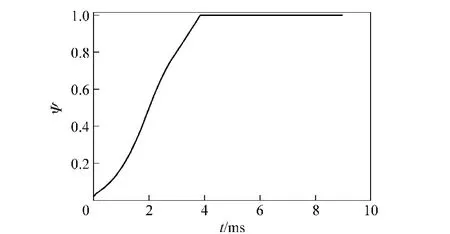
Fig.7 Powder burning percentage

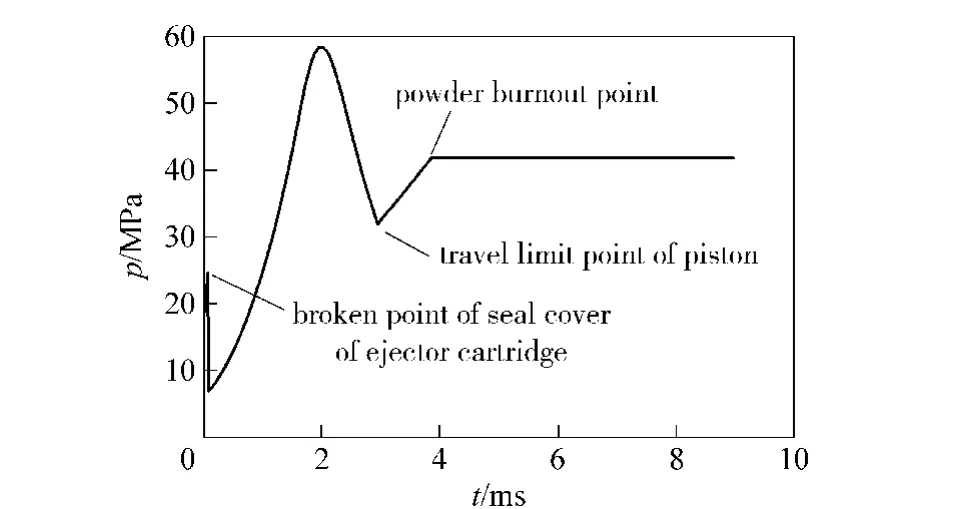
Fig.8 Gas pressure curve of powder

It can be seen from Fig.9 and Fig.10 that the velocities of submunition and reverse-ejection slow down under the resistance after the piston arrives at the travel limit.After an elapse of 3.34 ms，the submunition in the 7th segment is departed from the burning cabin at the velocity of －22.98 m/s，meanwhile，the velocity of reverse-ejection is 38.18 m/s.After an elapse of 8.98 ms，the submunition in the first segment is departed from the burning cabin at the velocity of－22.28 m/s and the process of dispersing is completed.At the moment，the velocity of reverse-ejection is 37.83 m/s.

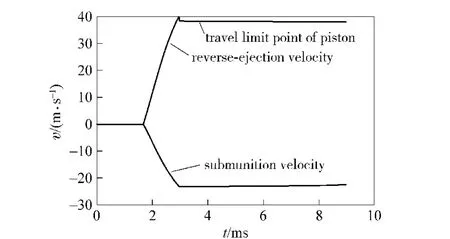
Fig.9 Dispensing velocities of submunition and reverseejection body in shell body axis system

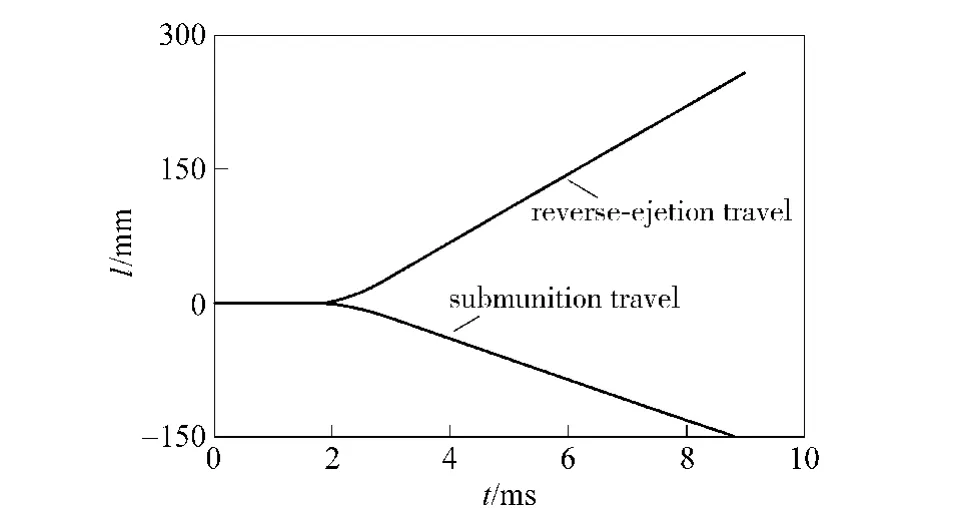
Fig.10 Travels of submunition and reverse-ejection body in shell body axis system

The velocity and location of submunition inO'xyzcan be calculated based on the value inO'εη1ζ1.The velocity curves of submunition and reverse-ejection in the first segment shown in Fig.11.

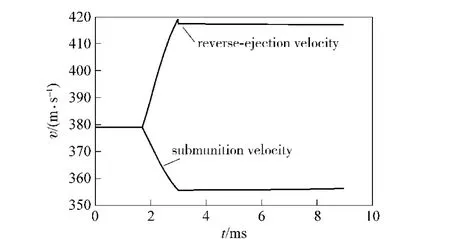
Fig.11 Velocities of submunition and reverse-ejection in earth axes

Fig.12 Trajectories of cluster munition and reverseejection in x－y plane of earth axes

The position curves of cluster munition and reverse-ejection inO'xyzwhen the submunition is dispersed and isn't dispersed shown in Fig.12.It can be seen from Fig.12 that the cluster munition system with piston dispersing mechanism is affected remarkably by the dispersing process.

The initial parameters of external ballistic trajectory can be calculated by using the said model，the parameters of cluster munition and the result of internal ballistic trajectory after dispersing.The external ballistic initial parameters of five submunitions of the second segment are calculated here.

It can be seen from the simulation results of static dispersing and dynamic dispersing that the velocity of static dispersing is different from the velocity of dynamic dispersing.So it is necessary to develop a dynamic dispersing model that focus on the piston dispersing mechanism.

4 Conclusion

A theory guidance is provided to design piston dispersing mechanism and analyze the dispersion of submunitions.

1)The dispersing internal ballistic model not only can be used to simulate the dispersing mechanism with travel limit，but also can be used to simulate the dispersing mechanism without travel limit which sets the travel limit value to be the length of cabin.

2)According to the particularity of dynamic dispersing，a novel internal ballistic model is developed，and the effect of reaction force on the cluster munition is discussed in detail.The cluster munition is fixed usually in the static experiment，so the mass of cluster munition is set to be a maximum.It is found from the comparison that the simulation result is in good agreement with the experimental value.

3)The model to calculate the initial parameters of submunition external ballistic trajectory not only can be used to calculate the parameter of piston dispersing，but also can be used to calculate the parameters of gas bag，central cartridge igniter and bellows dispersing.So the internal ballistic trajectory and external ballistic trajectory are connected by the model for the aerial dispersing.

4)Software based on the model is not only to simulate via system machine and loading parameters，but also to optimize the system machine and loading parameters and to instruct the dispersing machine design.

［1］ZHENG Ping-tai，LI Ai-li.A study of the interior ballistics of submunition dispensers with single and double combustion chambers［J］.Acta Armamentarii，2001，22(3):293－297.(in Chinese)

［2］JIN Zhi-ming.Gun interior ballistics［M］.Beijing:Beijing Institute of Technology Press，2004:9 － 80.(in Chinese)

［3］YANG Qi-ren.Flight dynamics of cargo projectile［M］.Beijing:National Defense Industry Press，1999:16 －91.(in Chinese)

［4］WENG Chun-sheng，WANG Hao.Computational interior ballistics［M］.Beijing:National Defense Industry Press，2006:1－62.(in Chinese)