高层建筑剪力墙力学性能的研究——连梁跨高比对双肢剪力墙动力特性的影响

杜玉峰

(西安建筑科技大学土木工程学院，陕西西安710055)

高层建筑的设计与建造不仅要考虑建筑的功能，还要考虑结构同时承受垂直荷载和水平荷载，抵抗地震的能力。随着建筑物高度的增加，框架结构柱子的合理截面已难以承担由于竖向荷载，特别是由水平荷载产生的内力。为了抵抗外荷载，需要不断地增大柱的截面，以致造成不合理的设计。用钢筋混凝土墙板(即剪力墙)来代替框架结构中的梁柱则能承担由各类荷载引起的内力，并能有效地控制结构的水平变形。

剪力墙是一种抵抗侧向力的结构单元。它具有较大刚度，在结构中往往承受水平力的大部分，成为一种有效的抗侧力的结构。在此结构中，墙是一平面构件，它除了承受沿其平面作用的水平剪力和弯矩外，还要承担竖向压力。在轴力、弯矩、剪力的复合状态下工作，其受水平力作用下似一底部嵌固于基础上的悬臂深梁。在地震或风载作用下，剪力墙除需满足刚度强度要求外，还必须满足非弹性变形反复循环下的延性、能量耗散和控制结构裂而不倒的要求。

1 高层建筑双肢剪力墙的简化计算

图1所示为双肢墙的几何参数，墙肢可以为矩形或T形截面，但均以形心线作为墙肢的轴线，连梁一般取矩形截面。利用连续连杆法计算双肢墙内力和位移时，基本假定如下。

(1)将墙体中每一层楼层处的连梁简化为在整个楼层高度上的连续杆。即把双肢墙原仅在楼层标高处通过有限个连梁连在一起的结构变成了沿整个高度上都是由无限个连续的连杆将两片墙肢连在一起的结构。这是为建立微分方程的需要而设的。

(2)忽略连系梁的轴向变形对墙肢水平位移的影响。即假定两个墙肢在同一标高处的水平位移是相等的。

(3)假定两个墙肢在同一标高处的转角与曲率都是相等的。因此连梁两端转角相等，连梁的反弯点位于连梁的跨中点。

(4)墙肢惯性矩I1、I2和连梁惯性矩 Ib，墙肢界面面积A1、A2和连梁截面面积Ab均为常数。这样建立的方程均为常微分方程，便于求解(如图1所示)。

1.理论学习。选择一些在语文教学领域中影响力较大的文章进行研读。例如在关于阅读教学的教研活动中，选择崔峦的《为了阅读教学的美丽转身》、夏丏尊的《阅读什么和怎样阅读》等文章来进行研读，从中学习先进的教学理论知识。

图1 双肢剪力墙简化示意

2 双肢剪力墙力学性能的有限元分析

2.1 结构计算模型

(1)问题定义:在进行有限元分析之前，首先对分析对象的形状、尺寸、工况条件、材料类型、计算内容等进行分析。本文研究的结构类型为弹性力学平面应力问题，分析类型为动力分析，分析内容为不规则开洞情况下剪力墙的频率。

(2)几何模型建立:几何模型是对分析对象形状和尺寸的描述，又称几何求解域。根据工程实例，对楼层的墙体，窗洞等进行简化处理。

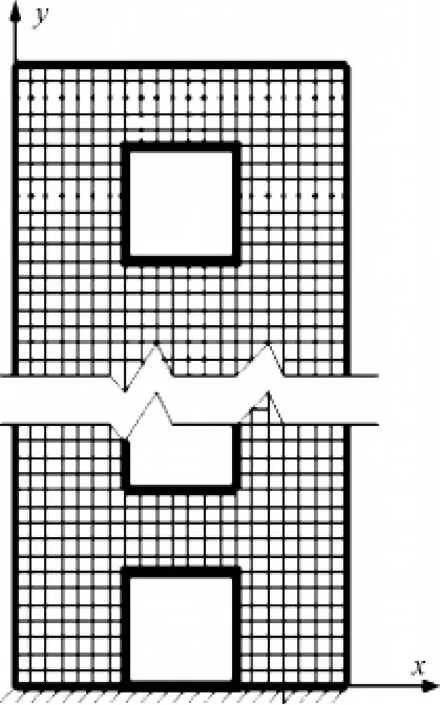
图2 剪力墙计算模型

(3)单元选择:计算单元类型采用平面二次矩形单元，材料为C30混凝土，弹性模量E=3.0×104N/(mm)2，泊 松 比 ν=0.1667

(4)网格划分:网格划分是建立有限元模型的中心工作，给出结构x方向与y方向的单元数，本程序具有自动划分网格的功能。对窗洞部分程序进行挖去处理，不计入总刚度矩阵(如图2所示)。

(5)边界条件的处理:通过分网生成的网格组合体定义了结点和单元数据，它并不是完整的有限元模型，因此还不能直接用于计算。在编制程序中对此问题进行了处理，结构的结点与单元编码顺序都为从左到右，从上到下，基础约束在解方程中采用划行划列法处理。

2.2 程序验证

为了验证程序计算结果的正确性，首先编写了一个计算整体小开口墙侧移问题的程序，并与简化计算结果相比较，其结果表现出较好的一致性。算例如下:

某高层住宅，层高3 m，具体尺寸如图3所示，采用C30混凝土现浇，求在图示水平荷载作用下的顶点水平位移。

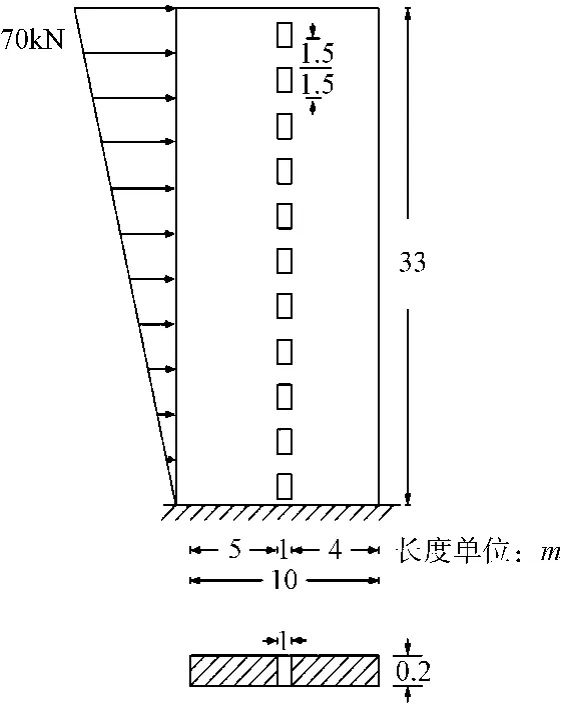
图3 简化计算模型

2.2.1 计算过程

解:判别剪力墙类型

窗洞总面积:Ad=1×1.5×11=16.5 m2

墙面总面积:A0=10×33=330 m2

洞口系数:ρ=Ad/A0=0.049

ρ=4.9%＜15%

且洞口长边尺寸小于洞边到墙边距离，不大于洞口间静距，故可按整体墙计算。

截面特征:

无洞口截面惯性矩:

等效抗弯刚度:

2.2.2 程序计算结果

当x方向划分单元数为20;y方向划分单元数为66时，顶点位移为0.00671m，与简化计算结果相比，误差为8.92%。

当x方向划分单元数为20;y方向划分单元数为110时，顶点位移为0.00652 m，与简化计算结果相比，误差为5.45%。

程序计算结果与简化计算结果相比较，误差较小，可以验证该程序算法正确性。

3 连梁跨高比对双肢剪力墙的影响

(1)当双肢剪力墙洞口大小为每层四个洞时，即连梁跨高比为1∶2时，由Matlab程序计算所得的双肢剪力墙六阶自由振动频率为(表1)

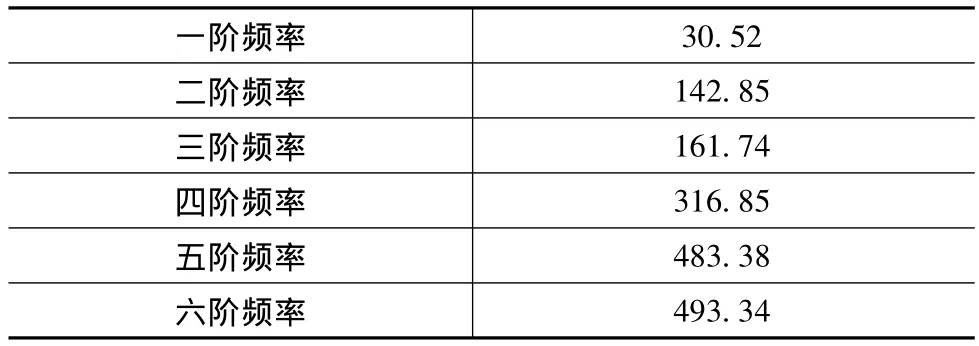
表1 计算结果(单位:Hz)

(2)当双肢剪力墙洞口大小为每层6个洞时，即连梁跨高比为1∶1.5时，由Matlab程序计算所得的双肢剪力墙六阶自由振动频率(表2)。

表2 计算结果(单位:Hz)

续表2

(3)当双肢剪力墙洞口大小为每层八个洞时，即连梁跨高比为1∶1时由Matlab程序计算所得的双肢剪力墙六阶自由振动频率为(表3)。

表3 计算结果(单位:Hz)

由以上结果比较可以看出，双肢剪力墙连梁跨高比对各阶频率都有影响，但是影响不是很明显。

4 结论与建议

(1)本文利用有限单元法对高层建筑剪力墙侧移进行了计算。通过与简化计算和MATLAB的计算结果对照分析，有限元计算结果与简化计算和MATLAB的计算结果吻合较好，误差较小，在10%以内。说明利用有限单元法分析双肢墙的可行性，本文的计算方法结果可靠，可以满足实际工程的需求。

(2)数值方法的计算精度。单元的数量直接影响计算结果的精确度。单元划分得越密，其计算精度越高，误差就越小。另一种方法是用高阶单元，本论文采用四结点矩形单元，比较适宜剪力墙等形状规整的结构，既能大大提高计算精度，又能很好地适应几何形状不规则的区域和边界，也较容易进行网格划分。

(3)高层建筑剪力墙在风荷载的作用下，双肢剪力墙连梁跨高比对各阶频率都有影响，但是影响不是很明显。

(4)剪力墙结构已成为现代建筑中一种重要的结构形式。而长期以来剪力墙的设计与分析一直采用经验公式与简化公式。但是这些方法存在很大的局限性。随着计算机的发展，有限元分析方法已成为一种重要并且行之有效的手段。尤其是对于大量的结构分析问题，有限元方法可以作为一种强有力的数值分析工具，诸如结构位移、应力、应变变化，破坏荷载等。这对研究结构的性能、改进工程设计都有重要意义。

[1]沈蒲生.高层建筑结构分析设计[M].北京:中国建筑工业出版社，2005

[2]梁启智.高层建筑结构分析与设计[M].广州:华南理工大学出版社，1992

[3]史庆轩，梁兴文.高层建筑结构设计[M].北京:科学出版社，2006

[4]王勖成，邵敏.有限单元法基本原理和数值计算[M].北京:清华大学出版社，1997

[5]王元汉，李丽娟，李银平.有限元法基础与程序设计[M].广州:华南理工大学出版社，2002

[6]朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社，1998

[7]赵西安.钢筋混凝土高层建筑结构设计[M].北京:中国建筑工业出版社，1992

[8]李海涛，邓樱.MATLAB程序设计教程[M].北京:高等教育出版社，2002

[9]Bungale S.Taranath.Steel，Concrete，and Composite Design of Tall Buildings(2nd，Ed.)

[10]edited by Sean Mackey.Symposium on the Design of High Buildings

[11]Nicholas Willems，William M.Lucas，JR，McGRAW－Hill Book Company.Structural Analysis for Engineer.1978

[12]Bungale S.Taranath，McGRAW－Hill Book Company.Structural Analysis and Design of Tall Building.1989