基于小波降噪的铁路边坡测斜监测分析

2011-07-24朱玉婷付平勇

四川建筑 2011年6期

刘伟，朱玉婷，付平勇

(华东交通大学道路与铁道工程重点实验室，江西南昌330013)

铁路边坡的深部水平侧移曲线时常锯齿状波动，一方面反映降雨、地震等自然环境因素或爆破、钻孔等人为施工因素作用使边坡内部位移产生突变，另一方面，反映监测信号由于电压不稳、电磁干扰等不良因素产生了噪声。为了提高铁路边坡稳定性监测与评价的准确性，有必要对采集的监测信号进行降噪处理[1，2]。小波分析作为一种有力的数学工具，具有多分辨分析的特点，在时频和频域都具有表征信号局部特征的能力，时间窗和频率窗都可以根据信号的具体形态动态调整，基于这些特征，小波分析可以广泛应用于监测信号降噪[3、4]。

1 小波降噪基本原理

利用小波分析降噪[5]－[7]，即在不同尺度下作小波变换，其实质是用不同中心频率的带通滤波器对信号进行滤波，以取得较好质量的信号。在实际的工程中，有用信号通常表现为比较平稳的信号或低频信号，而噪声信号通常表现为高频信号。

设f(x)是观测点观测序列，采用Mallat算法，将信号分解成不同频率成分:

其中，信号在低频空间Vj上的投影为:

在高频空间Wj上的投影为:

Ajf(x)是信号f(x)的频率不超过2－j的成分，Djf(x)是频率介于 2－j与 2－j+1之间的成分。

上述小波分解式实际可以写成如下矩阵形式:

式中:j=1，2，…J;H=(hk－2n)，H 为尺度函数对应的低通滤波器;G=(gk－2n)，G为小波函数对应的带通滤波器;Cj为在2－j分辨率下的离散逼近;Dj为在2－j分辨率下的离散细节;{hk}k∈Z与{gk}k∈Z是一对离散正交镜像滤波器(低通和高通)，(4)式即为Mallat塔式分解算法。

Mallat重构算法:

其中，j=J，J－1，…，1，H*和 G*，分别为 H 和 G 的共轭。

小波分解与重构降噪法就是根据Mallat分解式(1)至式(3)，将含噪声的信号分解在不同的频带内，然后，在信号重构时，将与噪声相应的高频细节信号有关部分Dj置零，重构信号便可达到降噪的目的。是f(x)经过滤波后的平滑信号表达式，即为提取的

?真实信号，这便是小波降噪的基本原理。因此信号降噪可分三步处理:首先对原始信号进行小波分解，则噪声通常含在高频系数中;然后对小波分解的高频系数以阈值等形式进行量化处理;最后再对信号重构即可达到降噪的目的。小波降噪的方法很多，如Mallat算法、小波变换模极大值法、非线性小波变换阈值法和平移不变量小波降噪法等，而小波变换模极大值法降噪和非线性小波变换阈值法降噪最为常用。

1.1 小波变换模极大值法

由于信号和噪声的小波变换系数在不同尺度上具有不同的传播特性，即随着尺度的增大，噪声所对应的模极大值迅速衰减。而信号的模极大值有三情形:若为缓变信号，则模极大值逐渐增大;若为阶越信号，则模极大值保持不变;若为脉冲信号，正、负极值组成的脉冲对的幅值将同时变小。于是，连续进行若干次小波分解后，综合各个尺度上模极大值的位置和幅值，可断定哪些模极大值是由噪声引起，哪些是由信号产生。去除噪声引起的模极大值，再重构剩余的模极大值，便可实现降噪。

1.2 非线性小波变换阈值法

非线性小波变换阈值法也称小波收缩。当信号的Lipschitz指数为正时，其小波变换极大值的幅度将随着尺度而增加;但噪声的Lipschitz指数为负时，则噪声所对应的小波变换模极大值将随尺度的增加而减少。利用这个特性，在不同的分解尺度上设置一定的阈值，将小于该阈值的模极大值点认为是噪声的小波变换引起的，将其置为零;大于该阈值的模极大值点则认为是信号小波变换引起的而予以保留。常见的阈值规则有sqtwolog规则、rigrsure规则、heursure规则和minimaxi规则。工程中常用的简单阈值处理法有非线性小波变换软阈值处理法、非线性小波变换硬阈值处理法等。

1.3 小波降噪的实现与性能评价

(1)为了选择较优的小波降噪方案，将涉及到小波函数、阈值的选择。实际工程中可根据自相似原则选取小波基函数，若选择的小波基函数与待处理信号有相似性，小波变换后，利于信号能量集中和减少计算量。土木工程[7]中关于测斜监测曲线，用Symlet、Coflet、Daubechies小波系均可实现曲线的降噪平滑，但以Daubechies小波系效果最优。对于阈值的选择，其实现十分简单，一个简单的方法就是用每个小波分解系数的幅值减去阈值，若差为负值则将系数设置为0;若差是正值则保持系数不变。在小波降噪方案实施过程中，同时也可以采用Matlab中的小波工具实现。Matlab中获取阈值的函数有:ddencmp、thselect、wbmpen、wdcbm;实现信号阈值去噪的函数有:wden、wdencmp、wthresh、wthcoef、wpthcoef、wpdencmp。

(2)为了对各种降噪方法进行比选，可用小波降噪的性能评价标准来评判，工程中常用的小波降噪的性能评价标准有信噪比(SNR)、信噪比增益(A)和均方根误差(RSME)，这三种评价标准是等价的[8]。其中信噪比是测量信号中噪声量度的传统方法，常被用来作为评价降噪效果的指标，信噪比越高则滤波效果越好，则降噪性能越好。信噪比单位是分贝，其定义为:

2 工程实例

以峰福铁路K294+680～K294+900段边坡CX－6测斜孔，从2010年12月至2011年3月(测量间隔为1周，共间隔16周)的水平位移监测数据作为小波降噪处理的对象，监测数据均通过某高科技实业有限公司CX－806B型数字显示滑动式钻孔测斜仪采集获得，并使用小波变换模极大值法、非线性小波变换软阈值法和非线性小波变换硬阈值法对所采集数据进行降噪处理，小波函数选择Db3，尺度选取3，阈值选取常用的hersure阈值，并用信噪比对降噪效果作对比，提取铁路边坡体内部水平变形的信息，进行铁路边坡测斜监测分析。

(1)边坡测斜布置

该测区属剥蚀低丘，边坡为土质边坡，山体自然坡度20°～30°，植被发育，线路沿水口库区北岸行走，整个病害长度约为300 m，包括一段路堑及其两端各一段路堤。根据路段地形地貌及地质情况，布置2排共6个测斜孔，其中一排布置在左侧路堑坡顶以上的山坡上，且位于已有纵向裂缝的下方，测孔间距50 m，布置有 CX－2、CX－6、CX－13 与 CX－7四个测孔;另一排布置在路堑右侧水沟外侧，布置有CX－1和CX－9两个测孔，布置见图1所示。

图1 测斜孔位布置示意图

(2)数据采集与分析

待测斜管安装完，使用测斜仪进行预通并采集初读数，再按时进行其他测斜监测。下面列出峰福铁路K294边坡CX－6测斜孔采集的部分水平位移监测数据，并用小波变换模极大值法、非线性小波变换软阈值法与非线性小波变换硬阈值法三种方法对所采集数据进行降噪处理，降噪结果见表1。

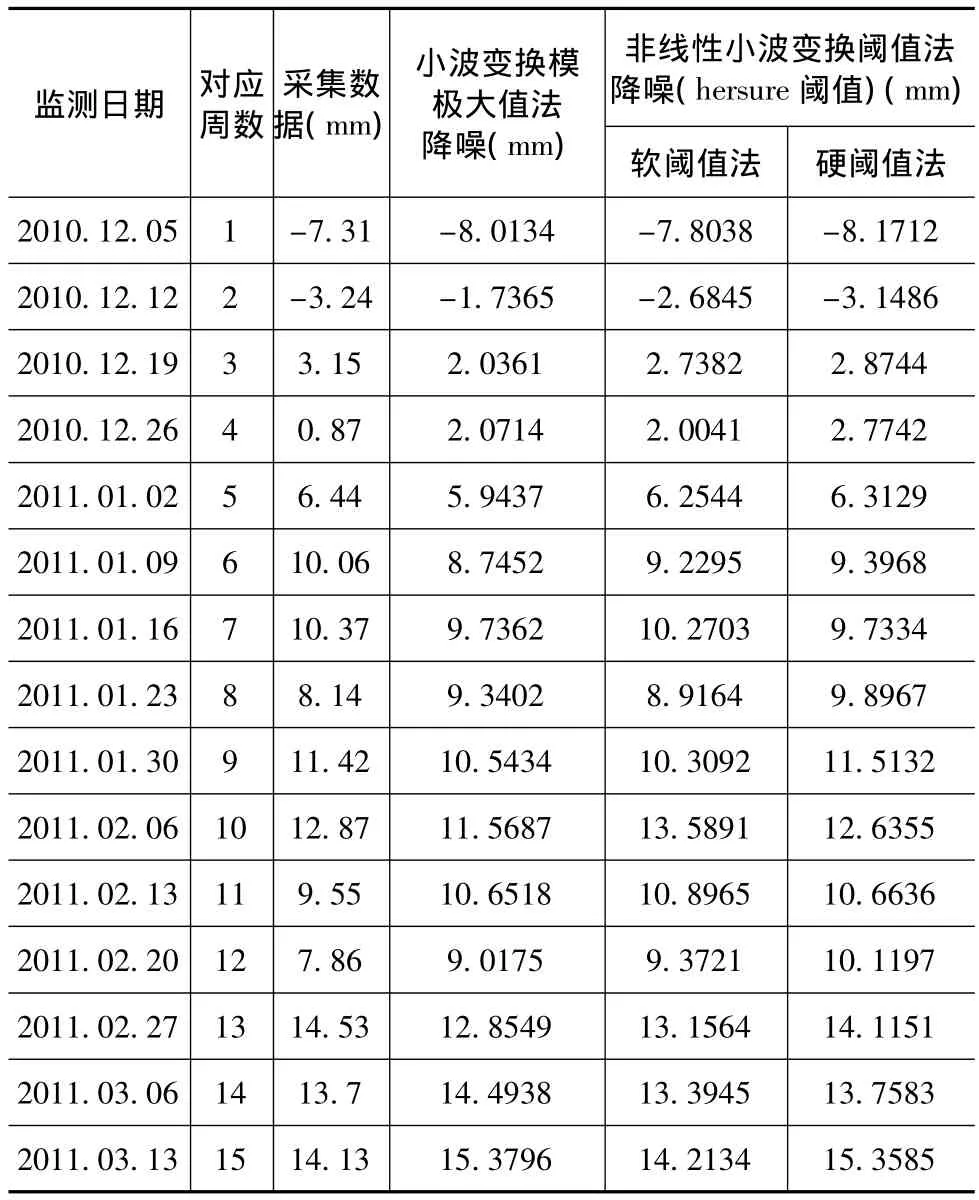
表1 CX－6测斜监测降噪处理结果

续表1

CX－6孔在第3、4、8、10与12周采集的原始数据有明显的波动，其中第4、10与12周表现较剧烈。通过降噪前后的数据结果对比，小波变换模极大值法、非线性小波变换软阈值法与非线性小波变换硬阈值法三种方法降噪效果都较明显，降噪后的数据穿行在原始数据之间。第4与12周时，小波变换模极大值法与非线性小波变换软阈值法降噪后的曲线，较非线性小波变换硬阈值法更好地保留了突变波动。

(3)边坡测斜降噪评价

由表1可见，非线性小波变换阈值法降噪的信噪比大于小波变换模极大值法;而在非线性小波变换阈值法中，又以非线性小波变换软阈值法的信噪比最高。由此可见，由于非线性小波变换软阈值法和小波变换模极大值法都建立在奇异性分析基础上，故降噪后的曲线对原始曲线中的尖峰和突变进行了有效地保持。但从曲线的平滑程度上看，小波变换模极大值法的平滑性优于非线性小波变换阈值法。同理，可对K294处边坡其他测斜孔的监测数据进行降噪。通过对其他各测孔采集得较多数据降噪处理效果对比验证，基于hersure阈值的非线性小波变换软阈值法更合理有效，能够敏感识别监测数据噪声和有用水平位移信息，更适合铁路边坡测斜监测分析。