基于模糊自适应控制的无轴承异步电动机SVM-DTC运行控制

刘贤兴，张文娟，万洛飞，杨泽斌

(江苏大学 电气信息工程学院，江苏 镇江 212013)

无轴承异步电动机作为一种集驱动与悬浮功能于一体的新型磁悬浮电动机[1]，由于悬浮控制绕组和转矩控制绕组同时叠绕在定子槽内，并以转矩控制绕组的旋转磁场作为产生悬浮力的偏置磁场，因此空间利用率和电磁效率等均有提高。

近几年，直接转矩控制越来越多地被用于无轴承异步电动机的控制中。传统的直接转矩控制借助的是Bang-Bang控制来实现PWM(Pulse Width Modulation)的控制策略，但脉动较大，开关频率不稳定。为减小脉动把空间矢量调制(Space Vector Modulation,SVM)技术应用到直接转矩控制中，可以大大减小转矩脉动和得到固定的开关频率。通常采用双PI调节可以获得电压参考矢量，但由于磁链和转矩的过程观测不准确导致PI调节器参数有偏差，使控制不准确[2-4]。

文中针对无轴承异步电动机的特点，提出了一种基于模糊自适应控制的SVM-DTC控制算法。在以定子磁场定向为基础的无轴承电动机数学模型下，通过模糊自适应控制器得到空间电压矢量。此方法可有效地抑制转矩、磁链脉动和转速超调，并能够获得稳定的逆变器开关频率。

1 无轴承异步电动机的数学模型

无轴承异步电动机的定子槽中同时嵌入了不同极对数的转矩绕组和悬浮绕组。当两绕组的极对数相差1时，转子能够稳定悬浮[5]。该电动机的数学模型[6]包括旋转部分和悬浮部分。

1.1 旋转部分数学模型

电压方程为

(1)

磁链方程为

(2)

转矩方程为

(3)

式中：R1s，R1r分别为定、转子电阻；ω1为d，q坐标系旋转速度；ωr为转子角速度；i1d，i1q分别为励磁电流分量；u1sd，u1sq，u1rd，u1rq分别为转矩绕组定、转子电压分量；Ψ1sd，Ψ1sq，Ψ1rd，Ψ1rq分别为定、转子磁链分量；i1sd，i1sq，i1rd，i1rq分别为定、转子电流分量；L1为转矩绕组自感；L1sl，L1rl为旋转绕组定子和转子漏感；Ψ1d，Ψ1q为气隙磁链分量；Te为电磁转矩；TL为负载转矩；J为转动惯量；p1为转矩绕组极对数。

1.2 悬浮部分数学模型

悬浮力方程为

(4)

式中：p2为悬浮绕组极对数；L2m为悬浮绕组互感；μ0为空气磁导率；l为电动机铁心长度；r为转子外径；i2sd，i2sq分别为定子电流分量；W1和W2分别为旋转、悬浮绕组中每一相串联绕组的有效匝数。

偏心磁拉力方程为

Fsx=ksx

Fsy=ksy，

(5)

运动方程为

(6)

2 SVM算法的实现

传统直接转矩控制中根据磁链、转矩滞环比较器的输出从开关表中选择合适的电压空间矢量对电动机的磁链和转矩进行控制。但可供选择的电压矢量始终是8个基本电压空间矢量，这很难完全补偿磁链和转矩的误差，会造成较大的脉动。如果根据磁链和转矩的误差，通过驱使误差为0的原则来选择参考电压矢量，并利用SVM合成该矢量，这样采样时刻的磁链和转矩误差在下一个控制周期得到补偿，因此可以大大减小脉动，使逆变器开关频率恒定。SVM的算法步骤为：

(1) 判断参考电压矢量Uref所在扇区；

(2) 计算开关电压矢量作用时间；

(3) 根据矢量作用时间合成PWM信号。

在图1中6个非零电压矢量将平面分为6个扇区。经过简单的加减及逻辑运算即可确定参考电压矢量所在扇区。这里假设参考电压矢量Uref在S1扇区，则可用相邻的电压矢量U4和U6来合成。usα，usβ分别为Uref在α，β坐标系中的分量。假定逆变器主电路直流母线电压为Udc，采样周期为Ts，矢量U4，U6和零矢量的作用时间分别为T4，T6和T0，则通过计算可得

图1 空间电压矢量及合成示意图

(7)

再对合成矢量的导通时间进行饱和判断，采用对称细分原则，并加入零矢量，用调制好的PWM波来控制电动机。

3 转矩和磁链的模糊自适应控制器设计

模糊自适应控制器是模糊控制系统的核心，决定系统的性能优劣[7-8](图2)。

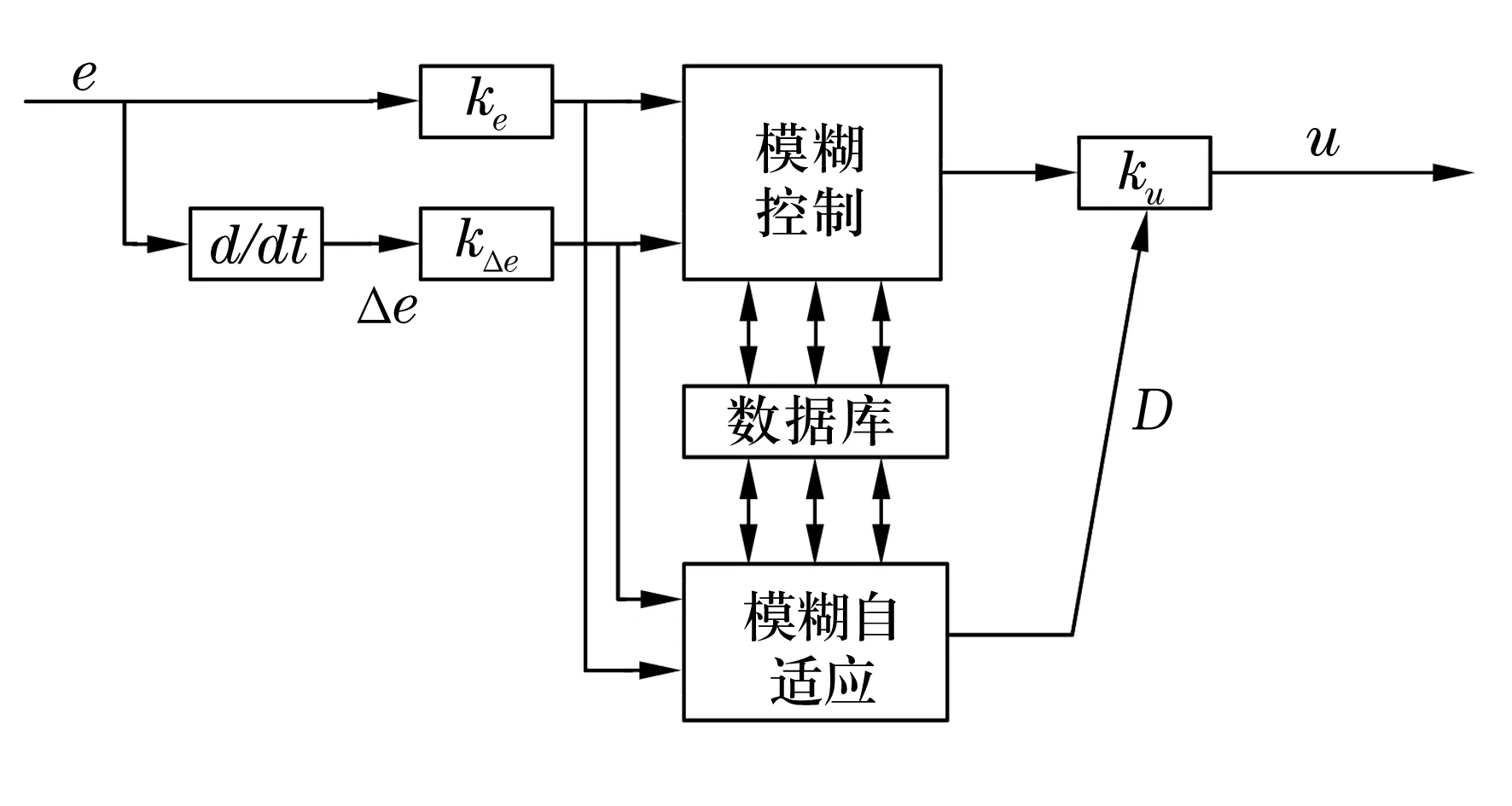
图2 模糊自适应控制器结构框图

3.1 变量的模糊化及隶属度函数

磁链模糊控制器根据磁链误差EФ、磁链误差变化率ΔEΦ以及相应的输出参考电压矢量的d轴分量Ud来定义其输入和输出变量。输入变量：EФ，ΔEΦ。输出变量：Ud。EΦ的模糊集为{N,Z,P};ΔEΦ的模糊集为{N,Z,P};Ud的模糊集为{NL,NS,Z,PS,PL}。其中：P表示“正”；Z表示“零”；N表示“负”；L表示“大”；S表示“小”。其输入及输出模糊变量的隶属度函数如图3所示。

图3 磁链模糊控制器输入、输出隶属度函数

同理定义转矩模糊控制器的输入、输出变量。输入变量：转矩误差ET和转矩误差变化率ΔET。输出变量：参考电压矢量的q轴分量Uq。ET的模糊集为{NL,NS,Z,PS,PL}；ΔET的模糊集为{N,Z,P}；Uq的模糊集为{NL,NS,Z,PS,PL}。其输入及输出的模糊变量隶属度函数与磁链模糊控制器输入输出隶属度函数相同。

3.2 模糊控制规则的建立

根据直接转矩系统的控制原理，当转矩和磁链的误差值在滞环比较器的范围内，通过比较差值与设定容差值之间的大小关系从而发出‘0’或‘1’的信号来说明需要增大还是减小定子磁链。发出的信号决定电压空间矢量的选择，从而实现直接转矩控制。如图1所示，设磁链矢量在S2扇区并且顺时针旋转，当磁链、转矩误差正向较大时(磁链、转矩比较器输出均为1)，为了减小定子磁链旋转速度以及幅值,选择电压矢量为U3(011)。把此规律反映到磁链和转矩的电压矢量上，当有磁链误差为正(P)，且有磁链误差的变化率为正(P)时，输出的参考电压矢量d轴分量Ud为负大(NL);当转矩误差为正大(PL)，转矩误差变化率为正(P)时，输出的参考电压矢量轴分量Uq为负大(NL)。根据这一规律可以得出磁链和转矩的模糊控制规则，见表1和表2。

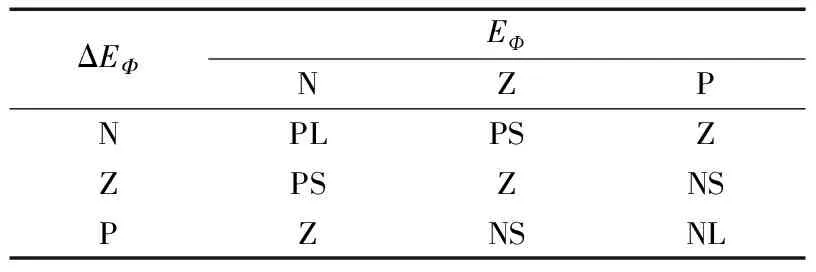
表1 磁链模糊控制规则

表2 转矩模糊控制规则

该规则适于空间矢量调制的直接转矩控制系统。模糊规则采用IF-THEN形式表示，磁链/转矩的第i条规则表示为

Ri:IFET=AiANDΔET=BjTHENUq=Cij

(8)

式中：Ai，Bj，Cij分别为EΦ/ET，ΔEФ/ΔET，Ud/Uq的子集变量。磁链模糊控制器有9条规则，转矩模糊控制器有15条规则。

3.3 模糊化与清晰化

磁链/转矩模糊控制器均采用Mamdani模糊推理法，第i条规则所对应的模糊关系为

(9)

由于模糊推理得到的控制量是一个模糊集合，而且被控对象只能接受精确的控制量，因此必须经过清晰化处理，将模糊控制量采用重心法转化成精确量实现控制。

3.4 自适应环节的设计

在模糊控制器中，由于比例因子ku的固定存在，使模糊控制器的输出不能很好地适应系统的变参数和非线性特性。ku的大小反映了系统的总放大倍数。在动态阶段，ku越大响应越快，但是容易超调。稳态时，ku过大会引起系统震荡，过小又会让系统的快速性变差。因此引入模糊增益调整因子D在线调整比例因子。给定量与真实值之间的偏差eD，偏差的变化率ΔeD和输出D的模糊变量分别定义为ED，ΔED和UD。输入变量模糊子集的隶属度函数分别与对应的磁链/转矩模糊控制器的隶属度函数一致。这里只需定义输出变量的模糊集。定义磁链模糊自适应控制器模糊输出量UФΦ的模糊子集为5个，语言值定义为：{Z(零),S(小),MB(中大),B(大),VB(非常大)}；同理定义转矩模糊自适应控制器模糊输出量UTT的模糊子集也为5个，语言值的定义同模糊输出量UФΦ一样。磁链自适应模糊输出变量的隶属度函数如图4所示；转矩自适应模糊输出变量的隶属度函数如图5所示。

图4 UФΦ的隶属度函数

图5 UTT的隶属度函数

其模糊控制规则见表3和表4。模糊推理一样采用Mamdani推理法。

表3 磁链自适应模糊控制规则

表4 转矩自适应模糊控制规则

4 基于模糊自适应控制的无轴承异步电动机的SVM-DTC控制框图

图6为无轴承异步电动机的总系统框图。在旋转子系统中，需要对定子电流、电压及转速进行测量，辨识出定子磁链、转矩以及相位角。这些量连同相应的给定量分别送入磁链和转矩的模糊自适应控制器中，通过模糊算法计算得出电压参考矢量在旋转坐标系下d，q轴上的分量usd和usq，结合辨识出的相位角进行坐标变换得出静止坐标系下的usα和usβ，一起送入SVM中，通过SVM的时间分配和合成得出合适的参考电压矢量，从而驱使误差为零。

悬浮子系统通过2个位置传感器，对x，y方向位移进行采样。径向位移的给定值与采样得到的反馈值的差值，经过PID调节器，可得到径向悬浮力的给定值。悬浮系统所需要的转矩绕组气隙磁链，可由直接转矩控制算法中已辨识好的定子磁链减去定子漏磁得到。将径向悬浮力的公式进行逆运算,进行力-电流计算可得出悬浮绕组定子电流i2α，i2β，再经过2/3变换和电流调节型逆变器(CRPWM)，驱动无轴承异步电动机的悬浮控制绕组。

5 仿真试验

利用Matlab/simulink工具箱，分别建立基于模糊自适应控制的SVM-DTC控制系统和双PI控制的SVM-DTC控制系统。仿真系统中所用的无轴承异步电动机参数为：转矩绕组额定功率P1=1 kW，额定转速n=3 000 r/min，定子电阻Rs1=2.01 Ω，转子电阻Rr1=11.48 Ω，定、转子互感Lm1=0.237 8 H，定子自感Ls1=0.242 4 H，转子自感Lr1=0.247 H，极对数p1=2；悬浮绕组额定功率P2=0.5 kW，定子电阻Rs2=1.03 Ω，转子电阻Rr2=0.075 Ω，定、转子互感Lm2=0.009 3 H，定子自感Ls2=0.012 H，转子自感Lr2=0.014 7 H，极对数p2=3。电动机转子质量m=2.85 kg，转动惯量J=0.007 69 kg·m2。

采用文中提出的算法对无轴承异步电动机系统进行仿真。系统的给定磁链为0.2 Wb，给定转速n=300 0 r/min，转子初始位移量均为200 μm，系统仿真时间为1.2 s，电动机的启动转矩为0，0.8 s时加负载转矩为1 N·m。仿真结果如图7所示。

从图7a可以看出，转子可以实现稳定的悬浮。图7b显示了较好的磁链圆。图7c为电动机的转速响应曲线，可以看出稳态时转速为3 000 r/min，系统跟踪效果良好。图7d为转矩响应曲线，转矩脉动很小，0.8 s突加负载1 N·m时转矩跟随性能良好。

图7 基于模糊自适应的无轴承异步电动机SVM-DTC控制系统仿真波形

图8a和图8b分别为基于模糊自适应控制和双PI控制的磁链脉动放大波形(仿真时间0.1～0.2 s)，从图中可以看出采用模糊自适应控制方法能有效地减小磁链脉动。脉动幅值从0.006 Wb减小到0.000 6 Wb。图8c和图8d分别为基于模糊自适应控制方法和基于双PI控制方法的转矩脉动放大图。通过对比可以看出采用模糊自适应控制方法能更好地减小转矩脉动，从0.15 N·m降低到了0.05 N·m。整个系统的可靠性得到提升。

图8 系统仿真波形对比

图9为基于模糊自适应控制的转速局部放大图(转速为2 995 ～3 005 r/min)，系统的超调量很小(小于2 r/min)。0.8 s突加负载时转速波动低于0.5 r/min。稳态时转速几乎没有误差。图10为转子径向位移对比图，可以看出转子x方向最大位移量从0.056 6 mm降到了0.054 5 mm。

图9 基于模糊自适应控制的转速局部放大图

图10 转子位移对比

6 结论

(1) 采用SVM-DTC控制，省去了复杂的运算。通过旋转部分的磁链辨识和计算可以得到悬浮部分所需要的气隙磁链。

(2) 基于模糊自适应控制的SVM-DTC系统，能实时在线调整参数，较PI调节器更为灵活，抑制转矩脉动能力更强。其突加负载对转速几乎没有影响，稳定性更优，转子的径向位移更小。设计电动机时可以减小气隙宽度，有利于定、转子之间的能量交换。

(3) 通过模糊控制实现了转矩和磁链的动态解耦，消除了彼此干扰，有利于系统控制。SVM算法恒定了逆变器的开关频率。