多种不确定因素环境下的最优产能决策研究
2011-07-24周昌林汪小京
程 亮,周昌林,汪小京
(宁波现代物流规划研究院物流组织与政策研究室,浙江宁波315042)
随着全球竞争的日趋激烈、产品快速开发能力的不断提高,以及顾客需求多样化和个性化的发展,使得准确地预测其销售产品的种类以及相应地规划产品和订单变得越来越困难。因此,在不确定的环境下,制造商需要在生产期初选择合适的产能,一方面要考虑尽可能地满足顾客需求,另一方面要避免产能过剩,节约投资成本。
基于以上实际问题背景,笔者考虑不确定环境下制造商的最优生产能力决策问题。具体而言,考虑有限计划期内,制造商的订单需求、生产及外包成本等要素都是随机变量,首先,在计划期初,制造商要确定一定的生产能力水平;然后,在计划期期间,通过生产备货方式满足下游顾客订单需求,并且当制造商的生产能力不够时,允许制造商采取外包方式满足下游订单需求,有限生产能力下的生产与外包模型如图1所示。

图1 有限生产能力下的生产与外包模型
与该研究相关的主要有两个方面的研究,一是生产能力优化研究。在初始能力规划研究方面,ATAY[1]、HOOD[2]研究了市场需求不确定情况下半导体制造企业的能力规划问题,建立了用于能力投资决策的随机整数规划模型;KARABUK[3]研究了面对市场需求和制造能力均不确定的情况下半导体制造企业的战略能力规划问题,依据市场销售和产品生产决策的分散化特性,构建了一个能力大小决策模型;潘景铭等以期望总成本最小化为目标函数,分别建立了不确定需求条件下供应链期望总成本与生产柔性之间的关系模型,并给出了最佳生产柔性的确定方法[4-5]。与以上研究不同,笔者同时考虑了多种不确定因素,包括随机需求、随机生产成本以及随外包成本,这与企业运作环境更相符,另外,笔者通过结合动态批量模型和Monte-Carlo模拟得到了生产商期望总成本与生产能力之间的关系。而与笔者研究相关的是动态批量研究,WAGNER和WHITIN[6〛首先考虑了确定需求环境下的动态补货决策模型(一般简称该模型为WW模型),得出最优的补货策略满足“零库存补货”规则,该规则是WW模型求解算法的基石。随后,大量文献对WW模型进行拓展,包括缺货等待、学习效应和易腐产品等方面,HSU[7]对动态批量问题做了一个比较全面的综述。将该研究中生产决策转换为补货决策,产能约束可以视为库存能力约束,因此,相近的文献主要是研究库存能力受限环境下的补货策略,LOVE[8]研究了固定库存能力条件下的补货模型,假设需求在缺货情况下完全等待,设计了一个O(T3)算法得到最优的补货策略。ATAMTÜRK和KÜÇÜKYAVUZ[9]研究了时变库存能力条件下的补货模型,假设不允许缺货发生,且库存成本中包括固定成本和线性持有成本,设计了一个O(T4)算法得到最优的补货策略。CHU[10]等研究了储存能力受限条件下的补货及外包模型,假设不允许存在缺货情况,设计了一个O(T2lb T)算法得到最优的补货以及外包策略。AKSEN[11]等研究了有限计划期内的补货及外包模型,当下一时期的销售价格远高于当期价格时,企业会采取外包方式满足当期需求,而将库存储备到下一时期从而获取更多的利润,并设计了一个O(T2)算法得到最优补货及外包策略。与以上文献不同,笔者不仅考虑了制造商的产能限制,而且考虑了外包策略,提出了一个多项式算法得到固定产能限制下的生产及外包策略,同时通过Monte-Carlo模拟得到多种不确定条件的最优生产能力。
1 模型构建
1.1 基本假设及参数定义
笔者主要考虑制造商在不确定环境下的最优生产能力决策问题。制造商拥有一定的生产能力,由于短期内不能扩大生产能力,制造商在整个计划期内生产能力保持不变,且生产提前期为零。另外,当制造商的库存发生缺货时,制造商将采取外包方式满足下游顾客的需求,且外包交货提前期为零。表1为符号及变量定义。

表1 符号及变量定义
与大多数动态批量研究假设相同,其假设如下:
(1)制造商的库存水平在计划期初和期末均为零,即I0=IT=0。
(2)制造商不允许缺货等待,所有下游零售商订单需求必须及时满足。
同时,笔者考虑存在多种不确定因素的环境下,假设在有限计划期内,与传统动态批量研究相反的假设如下:
(1)下游零售商需求为不确定的动态需求,服从均值为d,方差为φ的正态分布;
(2)制造商的单位外包成本st服从均匀分布,即
(3)制造商的单位生产成本ct服从均匀分布,即
1.2 模型构建
在有限生产能力条件下,制造商以最小化总成本为目标,包括总生产成本、外包成本和库存成本,具体分析如下:
(1)制造商在第t周期发生的总生产成本包括固定生产成本、变动生产成本和产能空闲成本:

(2)制造商在第t周期发生的外包成本为:

(3)制造商在第t周期内发生的库存成本为:

由此,可以得到制造商在整个计划期内的总成本为:

因此,在计划期T内,制造商首先确定生产能力P,然后在固定生产能力下优化每个周期的生产与外包决策(X={xt,1≤t≤T},Y={yt,1≤t≤T}),以最小化整个计划期内的期望总成本,故可以用以下数学模型表示:
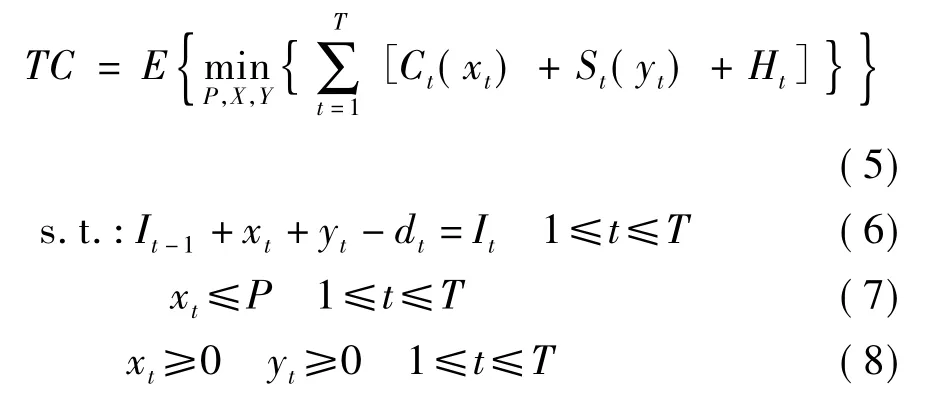
其中,约束等式(6)为制造商处库存水平的平衡关系,约束不等式(7)为制造商的生产量受到生产能力的限制,约束不等式(8)为制造商的生产或外包量均为非负值。
2 模型求解
2.1 最优生产与外包策略分析
由于生产能力限制,当期生产能力不能满足该生产周期内的订单需求,有可能充分利用上一生产周期内多余的生产能力,进行前期备货。例如:T=2;P=10;d=(5,15),K=0,最优生产策略X=(10,10),充分利用第一时期内的生产能力满足第二时期内大量的需求,这种情形在空调行业比较常见。因此,可以得到命题1。
命题1存在一个最优生产策略不一定满足It-1xt=0,I≤t≤T。
命题1说明零库存生产规则不一定成立,故采用传统WW模型和算法不能求解有限生产能力下的生产与外包批量策略。因此,笔者考虑零库存生产这种特殊的生产策略,定义C(i,j)为制造商在生产周期(i,j)内满足i,…,j-1期内下游零售商所有订单需求的最小成本,定义V(j)为制造商满足i,…,j-1期内下游零售商所有订单需求的最小成本,则V(T+1)为制造商在整个计划期T内的最小总成本。在零库存生产策略下,可以建立以下动态规划方程:
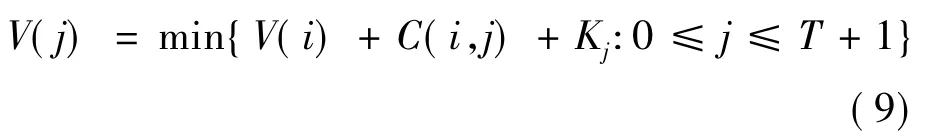
为优化计算,定义原点V(0)=0,有c=0,K0=0,h0=M,且假设cT+1=0,KT+1=0,hT+1=M,其中M为一个足够大的自然数。引入初始0阶段和T+1这两个阶段,是为了确保计划期期初和结尾阶段都发生补货需求,以优化计算整个计划期内成本。求解动态方程式(9)的关键之处在于求解生产周期(i,j)内的总成本,通过优化生产周期(i,j)内的生产及外包策略,得到C(i,j)。
命题2在生产周期(i,j)内,①若rk>0,采用生产备货方式依次满足集合Λ1={l1,l2,…,ln}中的订单需求,直至充分利用生产能力,超出生产能力部分采用外包方式满足;②若rk≤0,采用外包的方式满足 中的订单需求。根据命题2,分别考虑以下两种情况:


因此,根据以上分析,可以设计算法1得到最优生产及外包策略。
算法1固定生产能力条件下最优生产及外包策略。
初始化:V(0)=0,C(0,1)=0;
For j=1∶T+1
For i=1∶j-1
(1)在生产周期(i,j)内,权衡生产成本和外包成本,得到集合Λ1和Λ2;
(2)在集合Λ1和Λ2内,确定生产成本和外包成本;
(3)根据式(10)和式(11),计算C(i,j);
End
V(j)=min{V(i)+C(i,j)+Kj∶0≤j≤T+1};End得到最小总成本TC(P)=V(T+1)。
算法1包括两个循环,每个循环的计算复杂度至多为O(T),因此可得到命题3。
命题3在确定性环境下,算法1可以得到固定生产能力条件下最优生产及外包策略,且计算复杂度为O(T2)。
2.2 最优生产能力Monte-Carlo模型
考虑到下游零售商的订单需求、单位生产成本以及外包成本等多种因素都为随机变量,以下通过Monte-Carlo模拟方法,随机产生下游订单需求、生产及外包成本等参数,根据算法1得到随机参数设置环境下的最优生产及外包策略,进而得到不同生产能力下的总成本。最后,通过不断更新生产能力,得到不同生产能力下的总成本变化趋势,得到最小期望总成本下的最优生产能力,其模拟过程如图2所示。
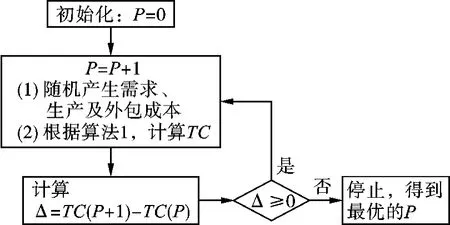
图2 Monte-Carlo模拟过程
根据图2中的模拟过程,可设计算法2得到最优的生产能力。
算法2随机环境下的最优生产能力。
步骤1:P=0,计算TC(P);
子步骤1:(1)根据正态分布随机产生订单需求D={dt,t=1,…,T};
(2)根据均匀分布随机产生生产成本C={ct,t=1,…,T};
(3)根据均匀分布随机产生外包成本S={st,t=1,…,T};
子步骤2:根据算法1,得最小总成本TC(P);
步骤2:Δ=TC(P+1)-TC(P),若 Δ>0,P=P+1,返回到步骤1;
否则,停止,得到最优的生产能力P*=P。
3 算例分析
考虑制造商未来一年(计划期T=12)的生产及外包决策问题。下游订单需求服从均值为15,方差为5的正态分布,即D=norm(15,5);生产成本为C=uniform(10,3),外包成本为C=uniform(12,2),生产能力闲置成本及其他参数设置如表2所示。
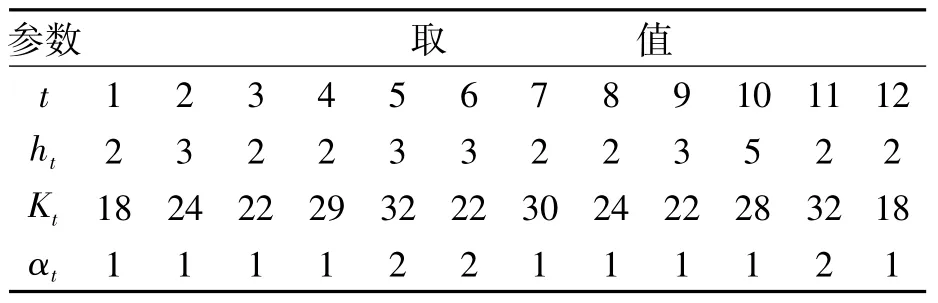
表2 制造的参数设置
通过模拟10 000次,得到不同生产能力下的期望总成本,如图3所示,产能设置在P*=18比较合适。若产能过小,大部分订单都需要通过外包完成,由于外包成本一般比单位制造成本更高,期望总成本在产能较小时会随着产能增大而减小;若产能增加到一定范围,产能对计划期内的运营总成本没有影响,但是由于存在一定的不确定因素,总成本会在一定范围内波动。
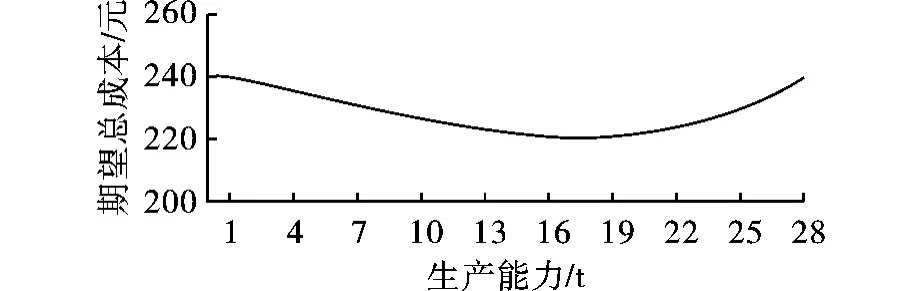
图3 不同产能下的期望总成本
图4 为不同需求环境下的最优产能设置,最优产能大小随着需求波动增大而增大,尤其是当外包成本比较高时,为了避免丢失订单,企业在面临波动较大的需求订单时需要设置更大的产能。
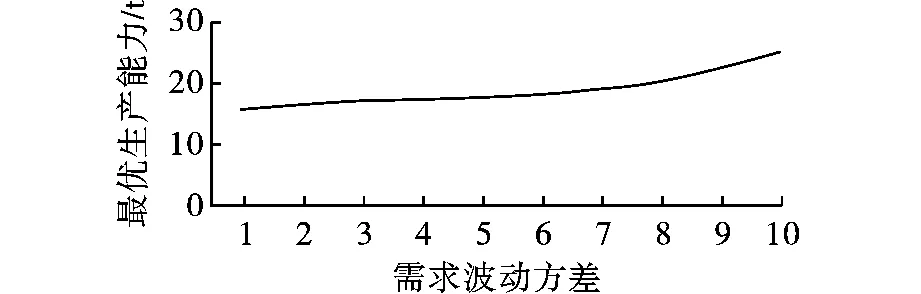
图4 不同需求波动下的最优产能
4 结论
笔者结合动态批量模型以及Monte-Carlo模拟两种方法,以最小化有限计划期内的期望总成本,优化总生产能力。动态批量模型较好地反映了制造商在确定性环境下的生产及外包计划,但该模型缺少对不确定性因素的反映。因此,考虑到涉及需求、生产及外包成本的不确定性,笔者将Monte-Carlo模拟方法融入到动态批量模型中,首先通过动态批量模型,提出了一个多项式算法得到固定生产能力条件下的最优生产及外包策略,并得到最小总成本;然后结合Monte-Carlo方法,通过数学实验得到制造商生产能力与成本及服务水平之间的关系,为企业在实际生产实践中提供借鉴。
[1]ATAY B,ERENGÜÇS S,VAKHARIA A J.Tool capacity planning in semiconductor manufacturing[J].Computers&Operations Research,2003,30(9):1349-1366.
[2]HOOD S J,BERMON S,BARAHONA F.Capacity planning under demand uncertainty for semiconductor manufacturing[J].IEEE Transactions on Semiconductor Manufacturing,2003,16(2):273-280.
[3]KARABUK S,DAVID SW.Coordinating strategic capacity planning in the semiconductor industry[J].Operations Research,2003,51(6):839-849.
[4]潘景铭,唐小我.需求不确定条件下柔性供应链生产决策模型及优化[J].控制与决策,2004,19(4):411-415.
[5]潘景铭,唐小我,倪得兵.供应链生产柔性有效边界研究[J].管理工程学报,2005,19(2):130-132.
[6]WAGNER H M,WHITIN TM.Dynamic version of the economic lot size model[J].Management Science,1958,5(1):89-97.
[7]HSU V N.Dynamic economic lot sizemodel with perishable inventory[J].Management Science,2000,47(6):1159-1169.
[8]LOVE S F.Bounded production and inventory models with piecewise concave costs[J].Management Science,1973,20(3):313-318.
[9]ATAMTÜRK A,KÜÇÜKYAVUZ S.Lot sizing with inventory bounds and fixed costs:polvhedral study and computation[J].Operations Research,2005,53(4):711-730.
[10]CHU F,CHU C.Single item dynamic lot-sizing models with bounded inventory and outsourcing[J].IEEE Transactions on Systems,Man,and Cybernetics-Part A:Systems and Humans,2008,38(1):70-77.
[11]AKSEN D,ALTINKEMER K,CHAND S.The single-item lot-sizing problem with immediate lost sales[J].European Journal of Operational Research,2003,147(3):558-566.
