基于销售协议的货运舱位控制竞争模型研究

2011-07-24徐月芳

武汉理工大学学报（信息与管理工程版） 2011年4期

罗咪，徐月芳

(南京航空航天大学民航学院，江苏南京210016)

收益管理是20世纪70年代末美国航空公司为了应对激烈的市场竞争而提出来的［1－2］。而今在激烈的航空运输市场竞争中，国内外众多航空公司已将收益管理运用到了航空客运上，并取得了不错的成效。航空货运收益管理在综合考虑销售时间和舱位容量对决策目标，即货运供给能力收益最大化影响的基础上，通过需求预测、动态定价和舱位控制策略，有效地解决由于货运舱位价值快速流失带来的价值意识风险问题，并为航空公司带来巨大收益，其核心是在合适的时间将合适的货运产品以合适的价格出售给合适的客户。

国内外已有不少学者对基于竞争的客运收益管理进行了研究。BELOBABA和WILSON［3］用模拟方法分析了只有两家航空公司在单航段市场竞争的情况。LI和OUM［4］就竞争环境下两家航空公司的舱位控制策略进行了研究，求出了完全信息下的对称均衡解。ZHAO和ATKINS［5］构建了竞争环境下仅具有一个舱位等级的两家航空公司的舱位控制策略模型。高强［6］在分析国内航空市场特点的基础上，通过构建博弈模型，研究了在竞争环境下的航空公司收益管理的舱位配置问题，分析了影响舱位控制的因素。罗利、彭际华［7］应用随机控制理论和博弈理论，建立了竞争市场环境下，两家航空公司的两个航班两级价格动态定价连续时间数学模型，给出了均衡解满足的条件，并探讨了模型求解的方法及相关性质。汪瑜、孙宏［8］构建了竞争环境下航空客运舱位控制的博弈模型，利用拉格朗日乘数法求解各航空公司最优低价票数，并以此来确定均衡舱位。

然而航空客运与货运的情况存在一定的差异，并不能直接套用客运的现有研究，但目前货运收益管理上关于竞争方面的研究几乎是空白。笔者结合国内航空货运的实际情况，研究了在竞争环境下各航空公司所采取的舱位控制策略，以航空公司利润均衡为目标建立了长期合同舱位分配的数学模型，以此确定在竞争情况下，各航空公司收益均衡状态的解。

1 假设条件及符号说明

(1)假设某一条航线上有n(n≥1)个航节，第1个航节是由航线起点至第1个经停点，第2个航节是由第1个经停点至第2个经停点，以此类推，第i个航节是由第i个航点到第i+1个航点，最后一个经停点至航线终点的航节则为第n个航节，(i=1，2，…，n)。n=1 时为直达航线，n ＞1时为联程航线。

(2)假设在上述航线上有m(m≥2)家航空公司共同经营，并且这些航空公司航班的起飞时刻、经停时刻和服务质量无显著差别。航空公司货舱不考虑体积，舱位量均以计费质量为标准，据IATA运价标准，货物的实际毛重和体积质量可用以计算货物航空运费的质量。换算标准为:体积质量=货物体积/6，一般情况下，取实际毛重或体积质量高者作为货物的计费质量［9］，不考虑旅客行李及邮件所占舱位质量，飞机腹舱的可载质量为 Wk(k=1，2，…，m)。

(3)航空公司面临两类需求:一类是具有较强议价能力的货运代理公司等大客户的舱位请求(暂称长期客户需求);另一类是议价能力差的小货运代理公司等零散客户的舱位请求(暂称临时客户需求)［10］。假设与长期客户签订了协议销售合同即成为协议客户。第k家航空公司在航节i上决定分配给长期客户的协议舱位量为WLki，剩余的舱位为临时舱位，令其为各航空公司在航节i上的协议舱位的单位价格为而临时舱位单位价格为。又如假设条件(1)中所描述的，由于每航节的最大载运量固定，为方便求解，使Wki=Wk，因而令各航节之间相互独立，无相关性。

(4)该模型中，航空公司的成本忽略不计。

(6)当协议客户的需求舱位大于航空公司所提供的协议舱位时，存在一部分协议客户愿意选择购买临时舱位来运输多余的货物，其在航节i上的意愿装载概率为αi。而当航空公司与协议客户签订的协议合同在此航线上所提供的舱位大于协议客户的需求舱位时，协议客户为了减少舱位虚耗，将剩余协议舱位提供给临时客户，由于协议客户与航空公司所提供的产品无差别，临时客户必定会转而购买协议客户提供的较低价位的舱位，直至剩余协议舱位提供完为止，才会选择购买临时舱位。

(7)虽然m家航空公司面对的市场是不确定的，但是他们对市场的需求预测具有一致性。各航空公司同时做出决策，并了解其他公司的策略。

2 货运舱位控制博弈模型的构建

为使各航空公司获得最大化收益，要在航空公司与长期客户之间的销售协议签订前确定分配给长期用户的协议舱位量。确定航空公司的协议舱位量必须考虑市场供需情况，对任一航节i的市场而言，均存在着如下3种情况。

(1)各航空公司所提供的协议舱位的总和小于长期协议客户需求舱位，即，此时各公司的协议舱位全部使用，而客户对临时舱位的需求则由两部分组成，一是临时客户的舱位需求，二是协议客户在航空公司提供的协议舱位装载满之后仍剩余部分货物未能装入协议舱位，而长期协议客户会考虑是否愿意按照临时舱位价格将剩余货物装入腹舱或是等待下一个航班到来，将剩余货物装入。因而在此存在一个协议客户的意愿装载概率αi，即有αi的概率，协议客户愿意将货物装载入同一航班的临时舱位。基于上述情况，第k家航空公司在航节i的收益期望为:

(2)各航空公司设定的协议合同舱位的总和大于等于临时客户需求舱位但小于市场总需求，协议客户签订的预留舱位是确定的，航空货运所提供的产品与航空客运一样具有易失性，一旦航班起飞，产品立即生效，至目的地降落交付客户后失效，因而，协议客户为减少损失，将剩余舱位转卖给临时客户，但由于协议舱位提供量小于整个市场的需求量，因而，没有购买到剩余协议舱位的临时客户仍旧会购买临时舱位，在此情况下，第k家航空公司在航节i的收益期望为:

(3)各航空公司的协议舱位提供量大于整个市场的需求量，即，此时，所有临时客户均能购得剩余协议舱位，而航空公司获得的收益则是协议客户必须支付的协议舱位费用。此时，第k家航空公司在航节i的收益期望为:

i即，此时由于航空公司与

由此可知，第k家航空公司在航节i舱位情况只能是上述3种情况中的一种，三者不能同时存在，因而，第k家航空公司在航节i的收益期望为:

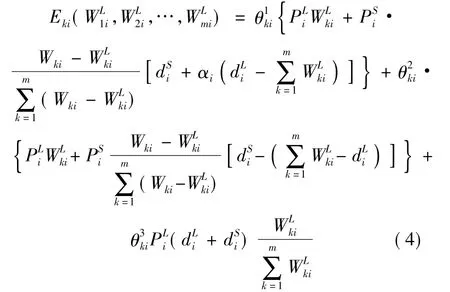
式中，

由于航线上有n个航节，则第k家航空公司的期望收益为:

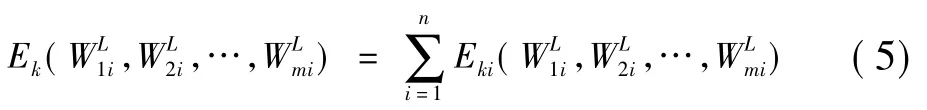
因此，取目标函数为第k家航空公司的航班收益，其优化模型如下:

3 求解过程

(1)处于完全信息静态博弈环境下，航空公司无法获得绝对的最大收益，只是根据对其他竞争公司采取的策略进行分析，获得博弈中的均衡解，此处的均衡为多维Nash均衡。由此可推出，当各航空公司在该航线上为直达航线时，多维Nash均衡则成为了Nash均衡;当各航空公司在此航线上为联程航线，但各航节之间无任何相关性时，所定义的多维Nash均衡实质是在各航节内独立博弈时得到的所有Nash均衡的简单组合。

(2)虽然该博弈中m个博弈方都有无限多种可选策略，因而无法用得益矩阵表示该博弈，但Nash均衡的概念还是适用的，即只要m个博弈方的一个策略组合满足其中的都是在航节i对于对方的最佳对策，就可以构成一个Nash均衡。根据Nash均衡的定义可知，Nash均衡就是具有相互最有对策性质的各博弈方策略组成的策略组合。因此，必是目标收益模型最大值问题式(7)的解。

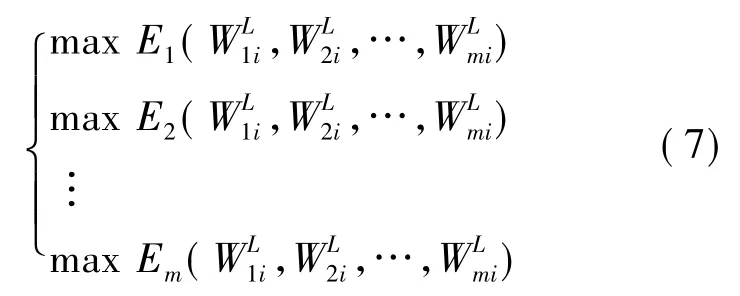
(3)对于该博弈，采用反应函数法，即对一个一般的博弈，只要得益是策略的多元连续函数，都可以求每个博弈方针对其他博弈方策略的最佳反应构成的函数，也就是反应函数，而解出的各博弈方反应函数的交点就是Nash均衡［11］。笔者所建模型是一个根据腹舱舱位供需关系建立的0－1规划模型，因而在建立反应函数时仍需考虑两种情况。首先对上述第k家航空公司的收益函数的第一种情况的偏导数使之为零，即:

联立这m个方程，可得出第k家航空公司的反应函数为:

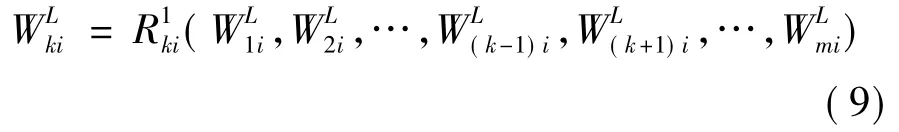
4 数据仿真

以南京—重庆—昆明的航线为例，该航线由3家航空公司共同经营。3家公司在该航线上所采用飞机机型均为A320，飞机腹舱最大可载质量分别为前舱3 402 kg、后舱4 536 kg、散货舱1 497 kg。假定行李邮件质量为3 000 kg，剩余最大可载质量为6 435 kg。为方便计算，假设南京至昆明航线的运费按照两航节相加原则进行，令3家公司在该航线上每次航班的货物可载质量为W1=W2=W3=6 000 kg。3家航空公司在同一航节上的单位价格具有一致性。其仿真参数如表1所示。

表1 仿真参数

按照求解过程采用Matlab软件进行编程求解，可得各航节各航空公司长期舱位分配量的仿真结果，如表2所示。再由固定的航班可载质量获得各航空公司在各航节的临时舱位分配量。各航空公司在南京至重庆航节上的收益为E11=E21=E31=13 055元，在重庆至昆明航节上收益为E12=E22=E32=28 138元。航空公司在整条航线上的收益为E1=E2=E3=41 193元。