基于CWAA算子的投资组合决策模型

苏克平，周礼刚，陈华友

(安徽大学数学科学学院，安徽合肥230039)

1952年，MARKOWITZ提出的证券投资组合的均值－方差模型［1］，推动了现代金融理论的发展。但从投资风险的本质属性、投资的效用函数、均值与方差的正相关性等多个角度，许多学者对用方差度量风险的科学性提出了质疑。文献［2］提出了下偏矩阵的概念，相对于方差度量风险，下偏矩阵作为风险度量指标具有明显的优势。但由于该方法结果的不确切性和计算方法的复杂性，使其没能得到广泛应用。文献［3］提出了用VaR度量风险的方法，但由于VaR不适用于市场的极端情况，其尾部损失测量非充分，且VaR方法中置信水平选择带有任意性，不满足一致性公理，因而文献［4］提出了CVaR方法，相对于VaR方法，CVaR方法满足次可加性，能够对尾部风险进行控制，具有良好的数学和统计特性。

1988年，YAGER提出有序加权平均算子(OWA)。这是一种介于最大算子与最小算子之间的信息集成方法，并广泛应用于群决策［5］、神经网络［6］、多目标决策［7］和数学规划［8］等诸多领域。文献［9］提出了组合加权算术平均算子(CWAA)，该算子通过控制平衡因子N和数据加权向量ω来控制目标函数，是OWA算子的推广。笔者基于CWAA算子，提出了CVaR度量下的组合投资决策模型，通过引入目标权衡因子ρ，将多目标模型转化为单目标混合整数规划模型。最后通过实例分析，说明了模型的可行性和有效性。

1 预备知识

定义1［10］在损失大于给定VaR值的条件下，该损失的平均值为条件风险价值，记为CVaR。

式中:VaRβ为置信水平为1－β的VaR值;x=(x1，x2，…，xN)T为投资 N 种风险资产的投资权重向量，满足为组合投资x的损失函数。

定义2设，若:

f～∶Rn→R

2 组合投资模型的建立

对组合投资问题，若用CVaR作为风险的度量工具，则最小化CVaR近似等价于最小化［11］:

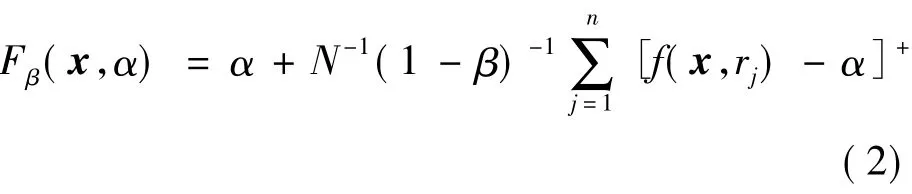
式中:n 为投资情景;x=(x1，x2，…，xN)T为投资N种风险资产的投资权重向量;N为投资组合中资产数目;α为VaR值;β为置信度;f(x，rj)为损益函数。

当r为一个已知分布的随机变量时，f(x，r)就是一个依赖于x的随机变量。在风险最小的情况下，要求收益最大，则任意投资策略下N种证券的预期收益为:

令:

若给定置信水平，要求风险损失最小，则有:

式中，zj≥f(x，rj) － α j=1，2，…，n。

同时，要使投资者的收益最大，即投资效用函数最大，则有:

再引入权衡因子ρ∈［0，1］，把双目标函数等价转化成单目标函数，其大小就反映了投资者在风险与收益之间的权衡，从而得到模型式(7):

令yki= 1 k＜j

0 k≥{j，则模型式(7)可转化为混

合整数规划模型式(8):

式中，K为任意大的整数。

该模型为混合整数规划模型，可用Matlab最优化工具箱求解。

若不考虑分红，即若pji为第i种风险资产在情形j下的价格，pj+Δti为第i种风险资产在情形j+Δt下的价格，rij为第i种风险资产在情形j下产生的收益率，E［ri］为第i种风险资产的期望收益率，则有:

故N种风险资产组合的损失函数［12］为:

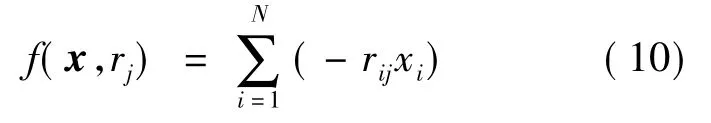
3 模型解的讨论

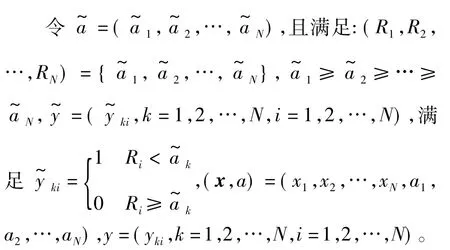
引理1 若(x，a)是模型式(7)的一个可行解，则存在 y=(yki，k=1，2，…，N，i=1，2，…，N)使得(x，a，y)是模型式(8)的可行解。

对于任意的(k，i)，若 Ri＜ ak，则 yki=1。由于K是任意大的整数，因此ak－Ri－Kyki≤0。若Ri≥ak，则 yki=0，ak－Ri－Kyki=ak－Ri≤0。

综上所述，(x，a，y)是模型式(8)的可行解。

引理2 若(x，a，y)是模型式(8)的最优解，则(x，)是模型式(7)的一个可行解。

引理3 若(x，a，y)是模型式(8)的最优解，则(x，，)也是模型式(8)的最优解。

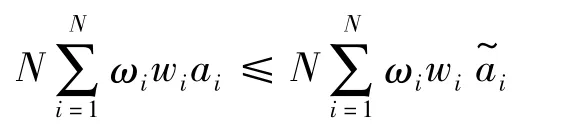
又由于(x，a，y)是最优解，则有:

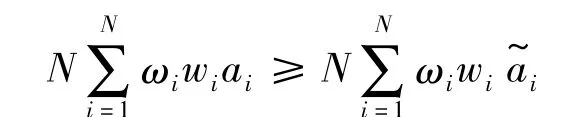
定理1 若(x，a)是模型式(7)的最优解，则存在y=yki使得(x，a，y)是模型式(8)的最优解。反之，若(x'，a'，y')是模型式(8)的最优解，则存在一个，使得(x'，)是模型式(7)的最优解。

证明 设(x，a)和(x'，a'，y')分别是模型式(7)和式(8)的最优解，构造 y=yki，其中由引理 1 知，(x，a，y)是模型式(8)的一个可行解，因此:

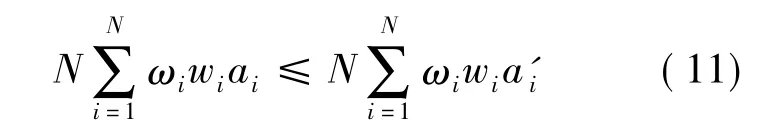
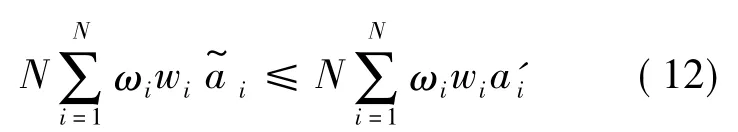
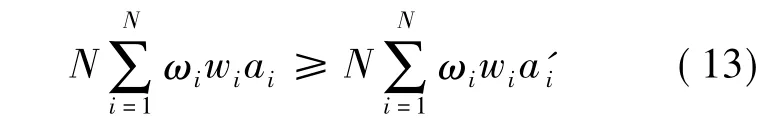
由式(11)～式(13)，可得:

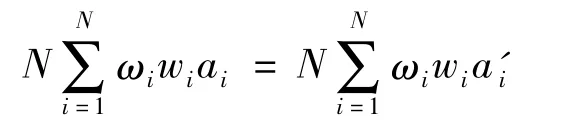
4 案例分析

为说明笔者建立模型的有效性，选取市场上6种证券5年的收益率数据，如表1所示。

表1 历史收益率的数据

将其代入式(8)，并设置信水平为95%，且ω =(1/6，1/6，…，1/6)T，运用 Matlab 求解模型如表2和表3所示。

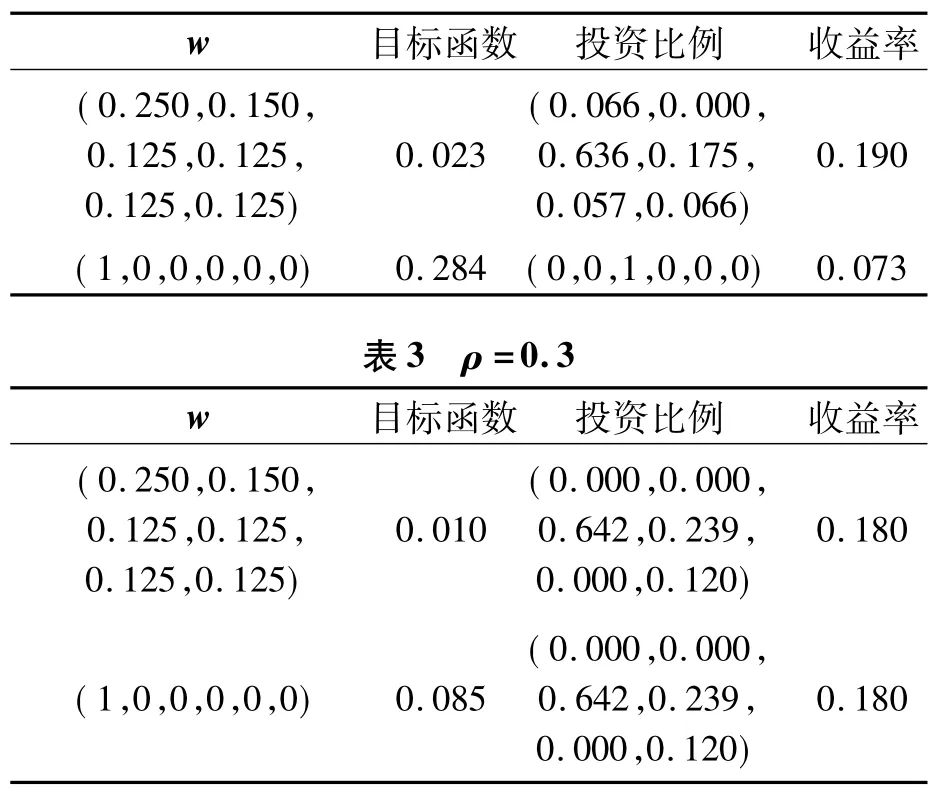
表2 ρ =0.7

由表2可知，在权衡系数较高时，如果投资者过分乐观，将会导致很严重的后果，如表2第3列所示:投资比例单一，收益率下降。因此，在这种情况下，投资者应该保持风险中性。由表3可知，在权衡系数较低时，投资者乐观与否对投资选择影响不大，权衡系数低，就意味着在运用该模型进行投资选择时考虑风险的重要性要比考虑收益大得多，前后的差异相互抵消。因而，权衡系数的引入对投资者个人的不理性而引起的极端行为起到了较好的预防和限制作用。

5 结论

笔者建立了CVaR度量基于CWAA算子的组合投资决策模型。引入的权衡系数，可以对个人不理性的极端行为进行约束，起到了较好的缓冲作用。关于CWAA算子相关联的向量和引入权衡系数和数据(α1，α2，…，αN)的加权向量，可根据实际投资背景具体设定。置信水平也可以根据实际需要重新设定。

［1］MARKOWITZH.Portfolio selection［J］.Journal of Finance，1952，7(1):77 －91.

［2］TSAI L H，HARLOW E，MEYERSON M.Isolation of the human cdk2 gene that encodes the cyclin and adenovirus associated p33 kinase［J］.Nature，1991(353):174－177.

［3］MORGAN JP.Risk metrics technical document［M］.4th ed.New York:Morgan Guaranty Trust Company，1996:214 －265..

［4］ROCKAFELLAR R T，URYASEV S.Optimization of conditional value at risk［J］.The Journal of Risk，2000，3(2):21 －44.

［5］CHICLANA F，HERRERA － VIEDMA E，HERRERA F，et al.Some induced ordered weighted averaging operators and their use for solving group decision－making problems based on fuzzy preference relations［J］.European Journal of Operational Research，2007，182(1):383－399.

［6］SUNG － BAE C.Fuzzy aggregation of modular neural networks with ordered weighted averaging operators［J］.International Journal of Approximate Reasoning，1995，13(4):359 －375.

［7］YAGER R R.On ordered weighted averaging aggregation operators inmulti－ criteria decision － making［J］.IEEE Trans Systems Man Cybernet，1988(18):183 －190.

［8］YAGER R R.Solvingmathematical programming problemswith OWA operators as objective functions［C］//Proceedings of the International Joint Conference of the Fourth IEEE Conference on Fuzzy Systems and Second International Fuzzy Engineering Symposium.［S.l.］:［s.n.］，1995:1441 －1446.

［9］徐泽水.几类多属性决策方法研究［D］.南京:东南大学图书馆，2003.

［10］ROCKAFELLAR R T，URYASEV S.Conditional value － at－ risk for general loss distributions［J］.Journal of Banking＆ Finance，2002(26):1443－1471.

［11］丁开敏.一类基于OWA算子的组合投资决策模型研究［D］.合肥:安徽大学图书馆，2009.

［12］徐志彬.基于CVaR的证券投资组合模型设计及其应用研究［D］.北京:华北电力大学图书馆，2009.