光滑核紧积分算子特征值的多尺度Galerkin快速算法*

陈 剑，曾泰山

(1.佛山科学技术学院理学院数学系，广东 佛山 528000；2.华南师范大学数学科学学院，广东 广州 510631)

设E:=[0,1], 记X：=L2(E), 算子K:X→X定义如下

其中K(t,s):E×E→R是一个光滑对称核, 即

K(t,s)∈Ck(E×E),K(t,s)=K(s,t)

于是,K为X上的自共轭紧算子K参看[1])。 考虑K的特征值问题：

Ku(t)=λu(t)

(1)

其中数λ和向量u∈X,u≠0 是待求的特征值和相应的特征向量。特征值问题具有广泛的实际应用背景, 在结构力学、工程设计、计算物理等诸多学科和技术领域都会遇到特征值问题。 设计一个有效的求解特征值问题的算法, 对科学计算和工程应用都有着巨大的意义。目前数值求解(1)的主要数值方法有: 有限元方法、(迭代)Galerkin方法、配置法、退化核方法以及外推法等等, 参看文献[2-8]。 本文运用多尺度Galerkin方法来近似求解(1)的特征值, 由于所用的多尺度正交小波基底具有消失矩和紧支集(参看[9-11]), 使得离散所得矩阵数值稀疏(绝大部分元素小的可以忽略不计), 从而可以实现矩阵压缩, 快速得到系数矩阵稀疏的线性方程组, 为后面矩阵特征值的求解提供极大的方便。

1 多尺度Galerkin格式

设Xn是L2(E)上的一个有限维子空间, 则求解 (1) 的 Galerkin 方法为：求数λn和向量un∈Xn,un≠0, 使得

(Kun,v)=λn(un,ν) ∀ν∈Xn

(2)

其中 (·,·) 表示空间L2(E) 上的内积。

设μ≥2是一正整数, 我们取Xn为以j/μn,j-1∈Zμn-1为节点次数小于k的分片多项式空间, 其中ZN:={0,1,…,N-1}, 显然dim(Xn)=kμn,Xn⊂Xn+1, 从而Xn可以写成Xn-1与其在Xn中的正交补空间Wn的直和。记w(i)为空间Wi的维数。按照文献[9-11]的构造方法, 我们得到Xn的一组具有k阶消失矩和紧支集的多尺度正交小波基{wi,j:(i,j)∈Un},其中Un:={(i,j):i∈Zn+1,j∈Zw(i)}。 利用多尺度小波基, 可以将(2)的特征向量表示成

(3)

其中ci,j是待求系数。 将上式代入方程(2)中, 得到多尺度Galerkin格式：

(4)

定义

Kn:=[(wi′,j′,Kwi,j)](i′,j′),(i,j)∈Un,

En:=[(wi′,j′,wi,j)](i′,j′),(i,j)∈Un,

Cn:=[ci,j:(i,j)∈Un]

于是方程(4)可导出如下线性方程组

(Kn-λnEn)Cn=0

(5)

2 矩阵压缩算法

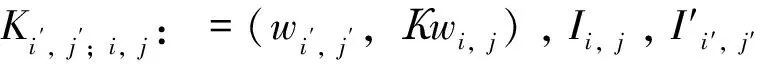
引理1 存在正常数c>0, 使得

(6)

其中p(t,·)和q(s,·)分别表示t和s的次数低于k的多项式,

(1-θ)k-1(1-θ')k-1dθdθ'

其中0<θ′<1,0<θ<1.由于K(t,s)∈Ck([0,1]×[0,1]), 则存在M>0使

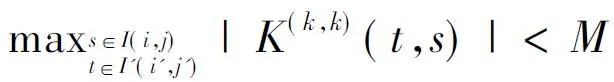
注意到wi,j和wi',j'具有k阶消失矩, 从而

引理得证。

上述引理表明, 当i+i′ 比较大时, 矩阵元素Ki′,j′;i,j的绝对值非常小, 这使得我们可以采用相应的截断策略。 为此, 我们将矩阵Kn按以下方式分块

Kn:=[Ki′,i]i′,i∈Zn+1

其中Ki′,i=[Ki′,j′;i,j]j′∈Zw(i′),j∈Zw(i)。对块矩阵Ki′,i我们给出如下压缩策略,并将压缩而产生的新的块矩阵记为

其中

(8)

(9)

(10)

3 压缩格式的收敛性和复杂性分析

引理2 存在一个与n无关的常数c>0,使得

‖Ki′,i‖2≤cμ-k(i+i′)

(11)

证明注意到w(i)～μi,w(i′)～μi′有

同理

于是

其中s(n)=dimXn=kμn。

证明对任意u,v∈L2[0,1], 有

其中P-1:=0。由Cauchy-Schwarz不等式可得

‖(Pi-Pi-1)u‖‖(Pi′-Pi′-1)v‖

注意到Pn为正交投影, 由引理2和截断策略(8)可知

‖(Pi-Pi-1)u‖‖(Pi′-Pi′-1)v‖≤

因为

记c=c′c″, 于是

cμ-nklog(s(n))‖u‖

引理获证。

从而

于是我们可以得到以下结论

定理1 存在一个与n无关的常数c>0, 使得

(12)

下面这个引理将在特征值误差估计中被用到, 是一个很有用的结论(参看[1])。

(13)

(14)

证明由引理4有

‖K-Kn‖=‖K-PnK‖=

因为u∈Hk(E),Pn为正交投影,K为紧算子, 从而

‖(K-PnK)u‖≤c′μ-kn‖u‖Hk:=c″μ-kn

于是

定理得证。

下面我们讨论压缩格式的计算复杂度。记

其中

Ei′,i=[(wi′,j′,wi,j)]j′∈Zw(i′),j∈Zw(i)

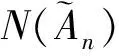
定理3 存在两个与n无关的常数c1>0,c2>0, 使得

从而

从而, 存在与n无关的常数c′>0, 使得

w(i′)×w(i)≤c′μi+i′

简单计算可得

定理得证。

4 数值算例

考虑如下积分算子的最大特征值逼近

W1的基底为：

图 1 采用截断策略需要计算的矩阵元素(n=10)

表 1 多尺度Galerkin方法的数值结果

Table 1 Numerical results of multiscale Galerkin method

n| λn-λ|Conv.RateComp.Rate22.174e-051.00031.385e-063.972 30.75048.732e-083.987 80.50055.489e-093.991 70.31263.447e-103.992 70.18772.165e-113.992 60.10981.359e-123.993 50.062 598.992e-143.918 40.035 1109.992e-153.169 60.019 5

参考文献：

[1]CHEN M, CHEN Z, CHEN G.Approximate solutions of operator equations [M].World Scientific Publishing Co, 1997.

[2]BABUSK I, OSBORN J.Eigenvalue problems, handbook of numercial analysis [M].II.Vol.llFinite Element Methods(PartI)，North-Holand, 1991.

[3]SLOAN I H.Iterated Galerkin method for eigenvalue problem [J].SIAM J Numer Anal, 1976, 13: 753-760.

[4]KULKARNI R P.A new superconvergent collocation method for eigenvalue problem [J].Comp Math, 2006,75: 847-857.

[5]CHEN Z, GNANESHWAR N, XU Y, et al.A fast collocation method for eigen-problems of weakly singular integral operators [J].J Sci Comput, 2009,41: 256-272.

[6]GNANESHWAR N.A degenerate kernel method for eigenvalue problems of compact integral operator [J].Adv Comput Math, 2007, 27: 339-354.

[7]KULKARNI R P.Use of extrapolation for improving the order of convergence of eigenelement approximations [J].IMA J Numer Anal, 1997,17: 271-284.

[8]CHEN Z, LONG G, GNANESHWAR N.Richardson extrapolation of iterated discrete projection methods for eigenvalue approximation [J].J Comp App Math, 2009, 223: 48-61.

[9]CHEN Z, MICCHELLI C A, XU Y.The Petrov-Galerkin methods for second kind integral equations II: multiwavelets scheme [J].Adv Comput Math, 1997, 7 : 199-233.

[10]黄敏.Fredholm第二型积分方程的小波Petrov-Galerkin算法[D].北京：中国科学院,2003.

[11]HUANG M.A construction of multiscale bases for Petrov-Galerkin methods for integral equations [J].Adv Comput Math, 2006, 25:7-22.